
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 10 minutes
Voting classifier is one of the most powerful methods of ensemble methods which we will explore in depth in this article. We will get a general idea about ensembling and then, dive in Voting classifier with a code example with SkLearn library.
When learning anything new or highly important, it is always a good practice to refer multiple resources before counting on that. Similarly, in case of a classification problem in machine learning, it is really good to make use of multiple models before taking any decision(especially in case of high value business decisions).
Here comes Sckitlearn Ensemble methods as a rescuer. The following are some of the other ensemble methods:
- Bagging
- Boosting
- Stacking
You can learn about them here
Question
Which of the following is not an ensemble method in scikit learn?
Voting Classifier
Voting classifier is one of the most powerful methods of ensemble methods. Many researchers and business people have adopted it because of the following nature.
1.Non-bias nature
2.Different models are taken into consideration
There are two types of voting classifier:
- Soft voting
- Hard voting
It takes the result of multiple classifiers and combines them in specific ways which we will explore now.
Voting
Voting represents the methodology we will be using to evaluate various models trained. There are two methods of voting:
01. Soft Voting
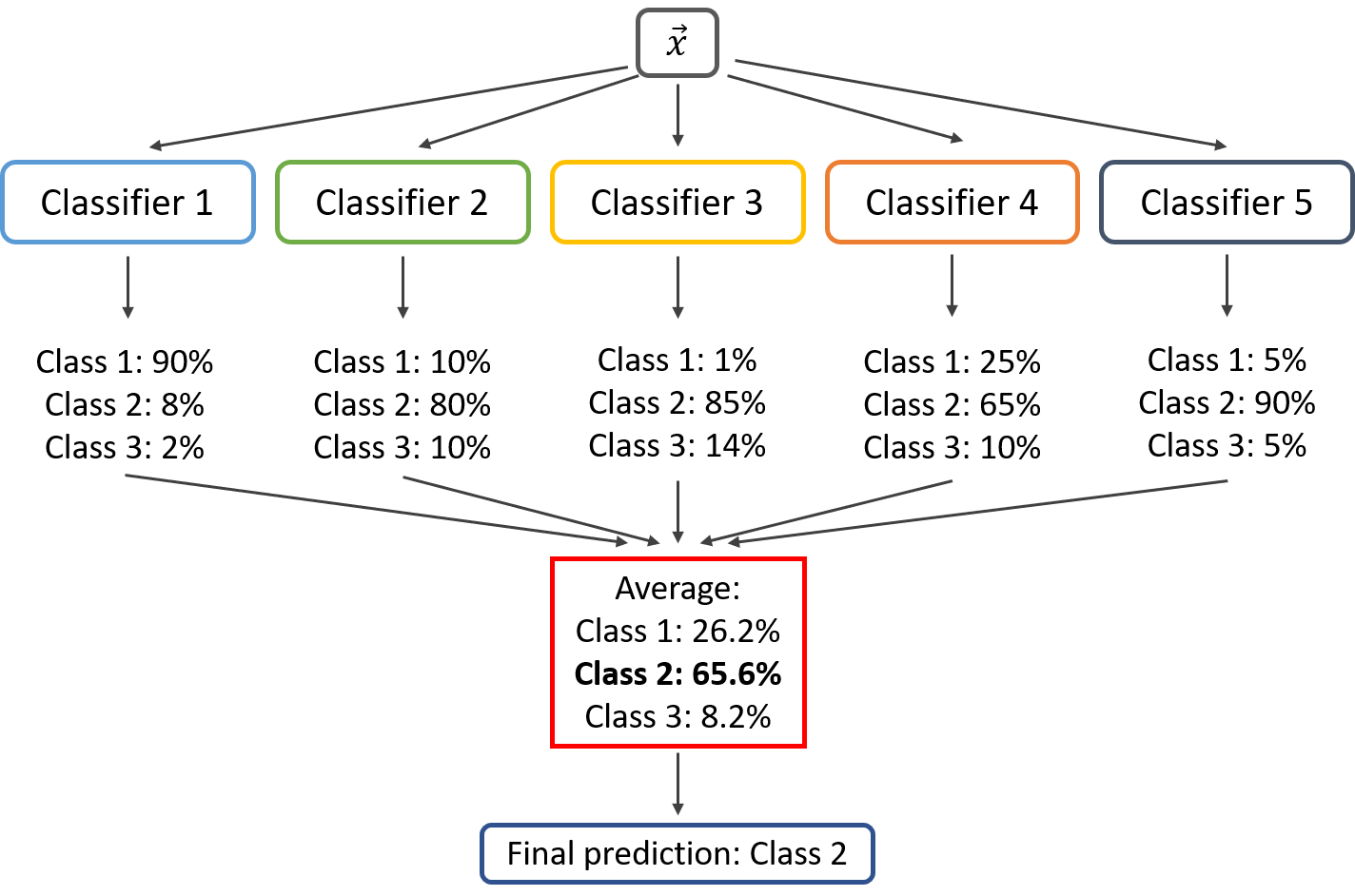
Here, the predicted probability vectors of each models are summed and averaged. The class with the highest value will be the winner and is given as output. Though this seems fair and logical, it is only recommended if the individual classifiers are well calibrated. This method is similar to finding the weighted average of a given set of values where each of the individual models have its proportionate contribution to the resultant output vector.
Consider the coding example. Let us assume that the prediction probability vector of LogisticRegression, SGDClassifier, bernoulliNBModel, KNeighborsClassifier, gaussianNBModel and multinomialNBModel be (0.1, 0.9), (0.3, 0.7), (0.2, 0.8), (0.3, 0.7), (0.5, 0.5) and (0.4, 0.6) respectively. Add all these vectors and take average in such way that the resultant vector has its first element equal to the average of all the first elements in the probability vectors and its second element equal to the average of all the second elements in each probability vectors.
Thus, this method harnesses the value, evaluation criteria and potential of each of the method used.
In the following image, the similar method is applied for a classification problem of three classes.
02. Hard Voting
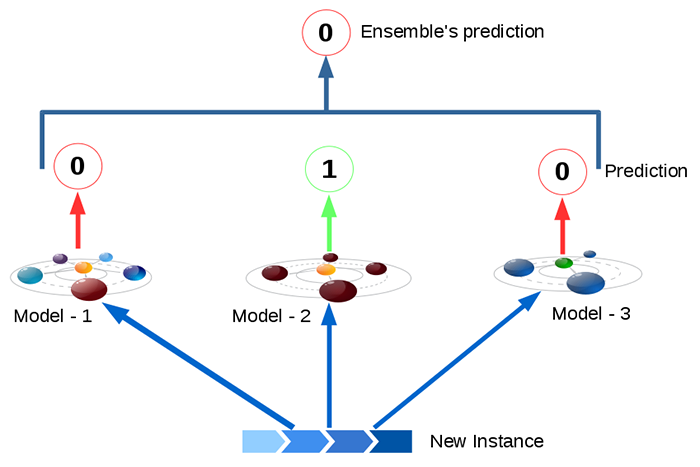
Here, the classification output of all the individual models are calculated and mode value of the combined output is given as the final output value. This kind of finding the desired output is analogous to to finding the arithmetic average of a given set of values because the individual probability values of each models are not considered. Only the output of each models are considered.
The main syntax for Voting Classifier is given below:
sklearn.ensemble.VotingClassifier(estimators=classifier, voting='hard')
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import MultinomialNB
from sklearn.ensemble import VotingClassifier
KNeighborsModel = KNeighborsClassifier(n_neighbors = 7,
weights = 'distance',
algorithm = 'brute')
KNeighborsModel.fit(X_train,y_train)
LogisticRegression = LogisticRegression(penalty='l2',
solver='saga',
random_state = 55)
LogisticRegression.fit(X_train,y_train)
gaussianNBModel = GaussianNB()
gaussianNBModel.fit(X_train,y_train)
multinomialNBModel = MultinomialNB(alpha=0.1)
multinomialNBModel.fit(X_train,y_train)
modelsNames = [('LogisticRegression',LogisticRegression),
('KNeighborsClassifier',KNeighborsClassifier),
('gaussianNBModel',gaussianNBModel),
('multinomialNBModel',multinomialNBModel)]
votingClassifier = VotingClassifier(voting = 'hard',estimators= modelsNames)
votingClassifier.fit(X_train,y_train)
Estimator
Estimator is a parameter used to invoke what are all the fitting model that we have used and clone them to power the Voting Classifier. It can be seen a list of books that we will be referencing(analogy to our example of books in introduction).It includes all the models that we want to perform voting classification. For example, look at the following code.
modelsNames = [('LogisticRegression',LogisticRegression),
('SGDClassifier',SGDClassifier),
('SVClassifier',SVClassifier),
('bernoulliNBModel',bernoulliNBModel),
('KNeighborsClassifier',KNeighborsClassifier),
('gaussianNBModel',gaussianNBModel),
('multinomialNBModel',multinomialNBModel)]
votingClassifier = VotingClassifier(voting = 'hard',estimators= modelsNames)
Question
Consider the given case and identify what type of voting classifier should be used. A biomedical engineer is developing a ML model to predict the trend of being affected by Diabetes mellitus. She has trained the model with Logistic Regression, Stochastic Gradient Descent Classifier, Bernoulli Naive Bayes Model, K - Neighbors Classifier, Gaussian Naive Bayes Model and Multinomial Naive Bayes Model. Now she is confused whether to use Hard Voting Classifier or Soft Voting Classifier. Can you help her in choosing the correct move.
Hint: In medical researches, high precision is required.
Advantages
Every machine learning classification model has its own advantages and disadvantages. By aggregating many models, we can overcome the disadvantages of each model to generalize the classification model.
But we have to be careful in choosing the different model. We have to make sure that they do not follow similar mathematical technique.
Conclusion
Voting classifier is a powerful method and can be a very good option when a single method shows bias towards a particular factor. This method can be used to derive a generalized fit of all the individual models. Whenever we feel less confidence on any one particular machine learning model, voting classifier is definitely a go-to option. Its applications ranges from high precision required places such as rocket science, medical science etc. and other conditions where high detailing is not mandatory.
