Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Principal Component Analysis (PCA) is one of the most fundamental algorithms for dimension reduction and is a foundation stone in Machine Learning. It has found use in a wide range of fields ranging from Neuroscience to Quantitative Finance with the most common application being Facial Recognition.

Some of the applications of Principal Component Analysis (PCA) are:

Spike-triggered covariance analysis in Neuroscience
Quantitative Finance
Image Compression
Facial Recognition
Other applications like Medical Data correlation

We will go through a basic introduction to PCA before going into each application in detail.

What is PCA?

Principal Component Analysis (PCA) is a dimensionality reduction technique invented by Karl Pearson in 1901, which is used for identification of a smaller number of uncorrelated variables known as Principal Components from a larger set of data. The figure below illustrates the same:

PCA

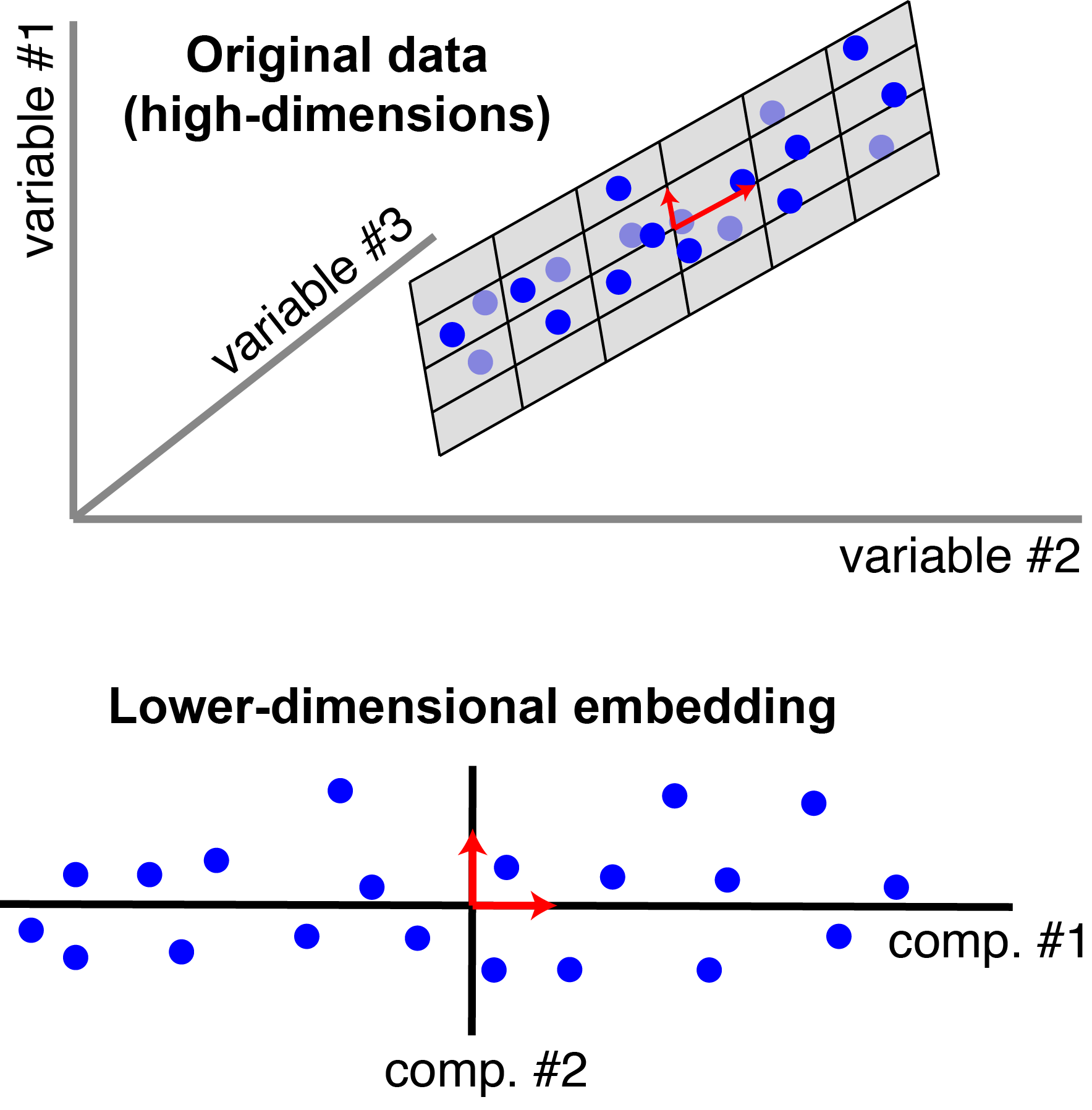
This articles focuses on the applications of PCA, hence it doesn't go into the details of why PCA works. However to understand why PCA works one can read OpenGenus IQ article: Why Principal Component Analysis (PCA) works?.

Get a deeper background on PCA:

Basic Ideas of Principal component analysis at OpenGenus
Algorithm of Principal Component Analysis (PCA) by Dakshya Mishra and OpenGenus
Why Principal Component Analysis (PCA) works? at OpenGenus

Applications of PCA

Now that we are done with understanding what PCA is and why PCA works we can focus on the applications of PCA. The principal application of PCA is dimension reduction. If you have high dimensional data, PCA allows you to reduce the dimensionality of your data so the bulk of the variation that exists in your data across many high dimensions is captured in fewer dimensions.

PCA is used abundantly in all forms of analysis - from Neuroscience to Quantitative Finance. PCA has wide-spread applications in various industries. The most significant applications of PCA are mentioned below:

1. Neuroscience:

A technique known as spike-triggered covariance analysis uses a variant of Principal Components Analysis in Neuroscience to identify the specific properties of a stimulus that increase a neuron's probability of generating an action potential.
PCA is also used to find the identity of a neuron from the shape of its action potential.
PCA as a dimension reduction technique is used detect coordinated activities of large neuronal ensembles. It has been used in determining collective variables, that is, order parameters, during phase transitions in the brain.

2. Quantitative Finance

PCA is a methodology to reduce the dimensionality of a complex problem. Say, a fund manager has 200 stocks in his portfolio. To analyze these stocks quantiatively a stock manager will require a co-relational matrix of the size 200 * 200, which makes the problem very complex.

However if he was to extract, 10 Principal Components which best represent the variance in the stocks best, this would reduce the complexity of problem while still explaining the movement of all 200 stocks. Some other applications of PCA include:

Analyzing the shape of the yield curve
Hedging fixed income portfolios
Implementation of interest rate models
Forecasting portfolio returns
Developing asset allocation algorithms
Developing long short equity trading algorithms

3. Image Compression

PCA is also used for image compression. Below mentioned is an example of Image Compression of the OpenGenus Logo using Principal Component Analysis.

Importing the required libraries:

import matplotlib.image as mpimg 
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA

Reading the Open Genus Logo as input:

img = mpimg.imread('opengenus_logo.png')

Printing the shape of the image:

print(img.shape) 
#Showing the image
plt.imshow(img)

Output:
(156, 194, 3)
opengenus_logo

Our image is in the form of 156 rows each containing 196 pixels which have 3 channels(RGB). We have to resize the image so that it is in the format required for PCA input. As 196*3=588, we resize the image to (156,582):

img_r = np.reshape(img, (156, 582)) 
print(img_r.shape)

Output:
(156, 582)

Running PCA with 32 Principal Components:

pca = PCA(32).fit(img_r) 
img_transformed = pca.transform(img_r) 
print(img_transformed.shape) 
print(np.sum(pca.explained_variance_ratio_) )

Output:
(156, 32)
0.98748475

With these 32 components we are able to express 98.7% of the variance.

Inverse transforming the PCA output and reshaping for visualization using imshow:

temp = pca.inverse_transform(img_transformed) 
print(temp.shape)
temp = np.reshape(temp, (156, 194 ,3)) 
print(temp.shape)

Output:
(156, 582)
(156, 194, 3)

plt.imshow(temp)

opengenus_logo_pca32

If we similarly compress images using 8, 16 and 64 Principle Components we are able to express the following percentages of variance of the original image:

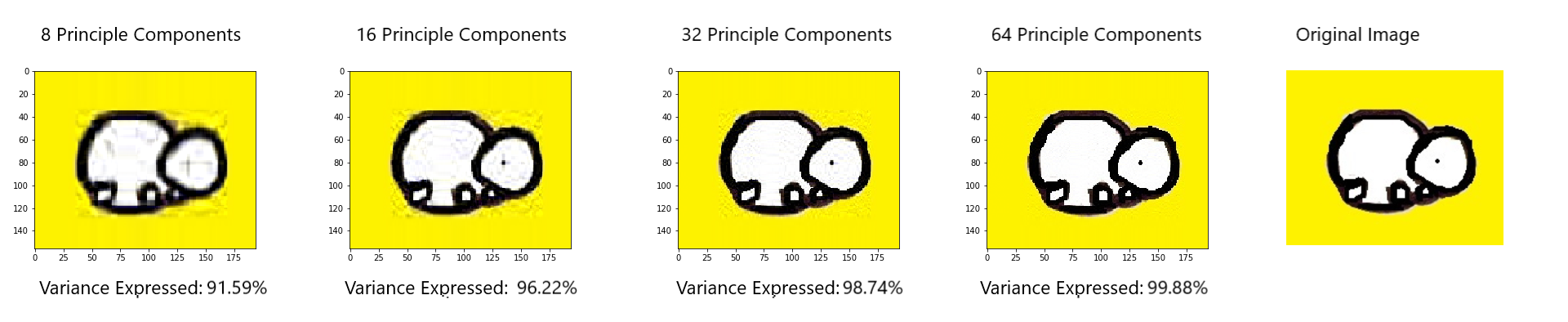
PCA_Image_Compression_figure-1

Number of Principal Components	Percentage of Variance Expressed
8	91.59%
16	96.22%
32	98.74%
64	99.88%

I highly recommend that you try to implement the above mentioned code yourself as well. The code along with the input image can be found on my Github account.

4. Facial Recognition

Using EigenFaces for Recognition of Faces is a quintessential technique in computer vision.Sirovich and Kirby (1987) showed that PCA could be used on a collection of face images to form a set of basis features.
PCA is at the heart of the EigenFaces approach as the set of EigenFaces is generated using PCA.
Eigenface approach reduces statistical complexity in face image representation.
Other researchers have increased face recognition accuracy by using a combination of Wavelet, PCA, and Neural Networks.

5. Other Applications

PCA has also been used in various other application which are mentioned below:

PCA has been used on Medical Data to show correlation of Cholesterol with low density lipo-protein.
PCA has been used on HVSR(horizontal to vertical spectral ratio) data aimed at the seismic characterization of earthquake prone areas.
PCA has been used in the Detection and Visualization of Computer Network Attacks.
PCA has been used in Anomaly Detection.

Applications of Principal Component Analysis (PCA)

Machine Learning (ML) principal component analysis