
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Hello everybody, I'll illustrate in this article two important concepts in our journey of neural networks and deep learning. Welcome to Backpropagation and Gradient Descent tutorial and the differences between the two.
Table of content:
- Difference between Backpropagation and Gradient Descent
- Recap how NN works
- Backpropagation algorithm
- Gradient Descent algorithm
- Types of Gradient Descent
1. Difference between Backpropagation and Gradient Descent
Following table summarizes the differences between Backpropagation and Gradient Descent
| Point | Backpropagation | Gradient Descent |
|---|---|---|
| Definition | the algorithm that is used to calculate the gradient of the loss function with respect to parameters of the neural network. | the optimisation algorithm that is used to find parameters that minimise the loss function. |
| Dependencies | Calculus and Chain rules | Backpropagation |
| Type of method | This is not a learning method | first order optimizer |
| Input size | Calculate the gradient for each single input-output example | may be Stochastic, batch or mini-batch |
| Sequence | come first | must be after backpropagation |
| Problems | None | may have some problems such as local minima and saddle point |
Moving forward, we will understand the two concepts deeper so that the above points in the table will make much more sense.
2. How NN works:
First of all, i'd like to name neural network as baby 'basiclly your baby' who you try your best to learn him well and of course he will learn through his all life by trial and correction his faults, exactly like your neural network.
You have input data and want to train your model on it but how ?
Let's say each sample of your data has 3 features and only one label (y)(of two classes), how the model will find the pattern between them?
Magically the answer will be backpropagation and gradient descent.
You will input your features into your model as (X1 ,X2, X3)
and each neurons of your model will randomly create weights multiplying them to Xs, adding bias,perform activation function and calculate outputs which enter the next layer of neurons, and this process occurs till the output layer where your model out a predicted label (y-hat).
This what is called feed Forward.
3. Backpropagation algorithm:
But what if your model predicted label (y-hat) away from the true label (y) of your data (and of course it's a normal phenomenon as your model at the first place randomly creates weights for its neurons). here role of loss function will come which calculate the difference between y and y-hat. Then the model now knows how much the difference between them and want to upgrade the weights of each neurons to decrease this difference. here the role of backpropagation will come which calculate how much exactly our weights need to be upgraded which we call it the gradient ( how our loss will change in respect of the weights ) and now it all about calculus but you don't need to be a genius in math to calculate it as now there are many frameworks that remove this hassle off your shoulder (like TensorFlow and PyTourch).
But if you want to dive into, so be with this:
This what NN does...
- z1 = W1.X + b1 (W is the weight, b is the bias)
- a1 = relu(z1) (relu is the activation function, a1 output of fist layer)
- z2 = W2.a1 +b2
- a2 = relu(z2)
- z3 = W3.a2 +b3
- y-hat = sigmoid(z3) (sigmoid is another activation function for binary classification as in our case)
- Loss (y-hat,y)
So we need to know what is the derivative of loss with respect to the weights so we can update the weight to improve the loss(decrease it) (dL/dW).
First we will use what is called the chain rule :
- dL/d(y-hat)
- dL/dz3 = dL/d(y-hat). d(y-hat)/dz3 (calculs of sigmoid equal yhat(1-yhat))
- dL/da2 = dL/dz3 . dz3/da2 (also dL/dW3 = dL/dz3.dz3/dW3(dz3/dW3 = a2))
- dL/dz2 = dL/da2 . da2/dz2
- dL/da1 = dL/dz2 . dz2/da1 (also dL/dW2 = dL/dz2.dz2/dW2(dz2/dW2 = a1))
- dL/dz1 = dL/da1 . da1/dz1
- dL/dW1 = dL/dz1 . dz1/dW1 (we can say dL/dW1 as dW1)
till now you probably know why it call backpropagation as we letterly back each step in feed forward propagation.
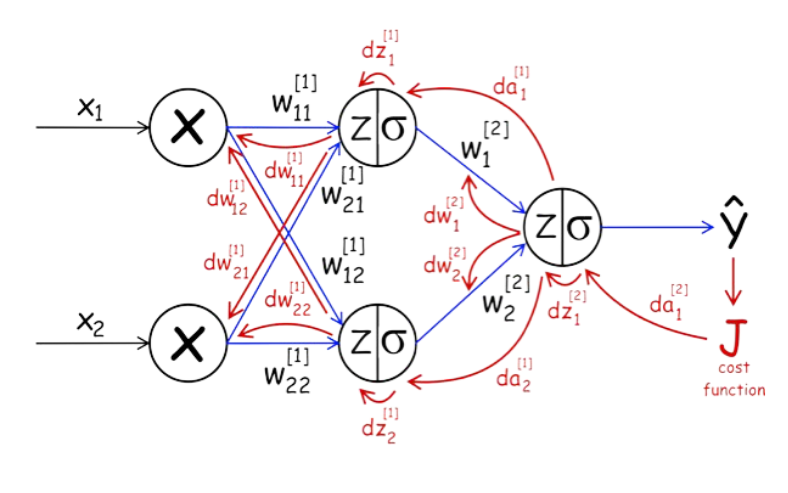
J(cost function) is another name of L(loss function)
4. Gradient Descent algorithm:
After we found our gradient, we will update our weights in the opposite direction to the gradient for our loss function to find the minimum value.
so W := W - learning rate * dW.
and b := b - learning rate * db.
We can say that the Gradient Descent algorithm is the optimization algorithm which tries to find the minimum value of the cost or loss function by taking steps in the opposite direction of the gradients. So if the gradient is positive, the model will decrease the weights where the gradient is negative, the model will increase the weights in order to decrease the total loss.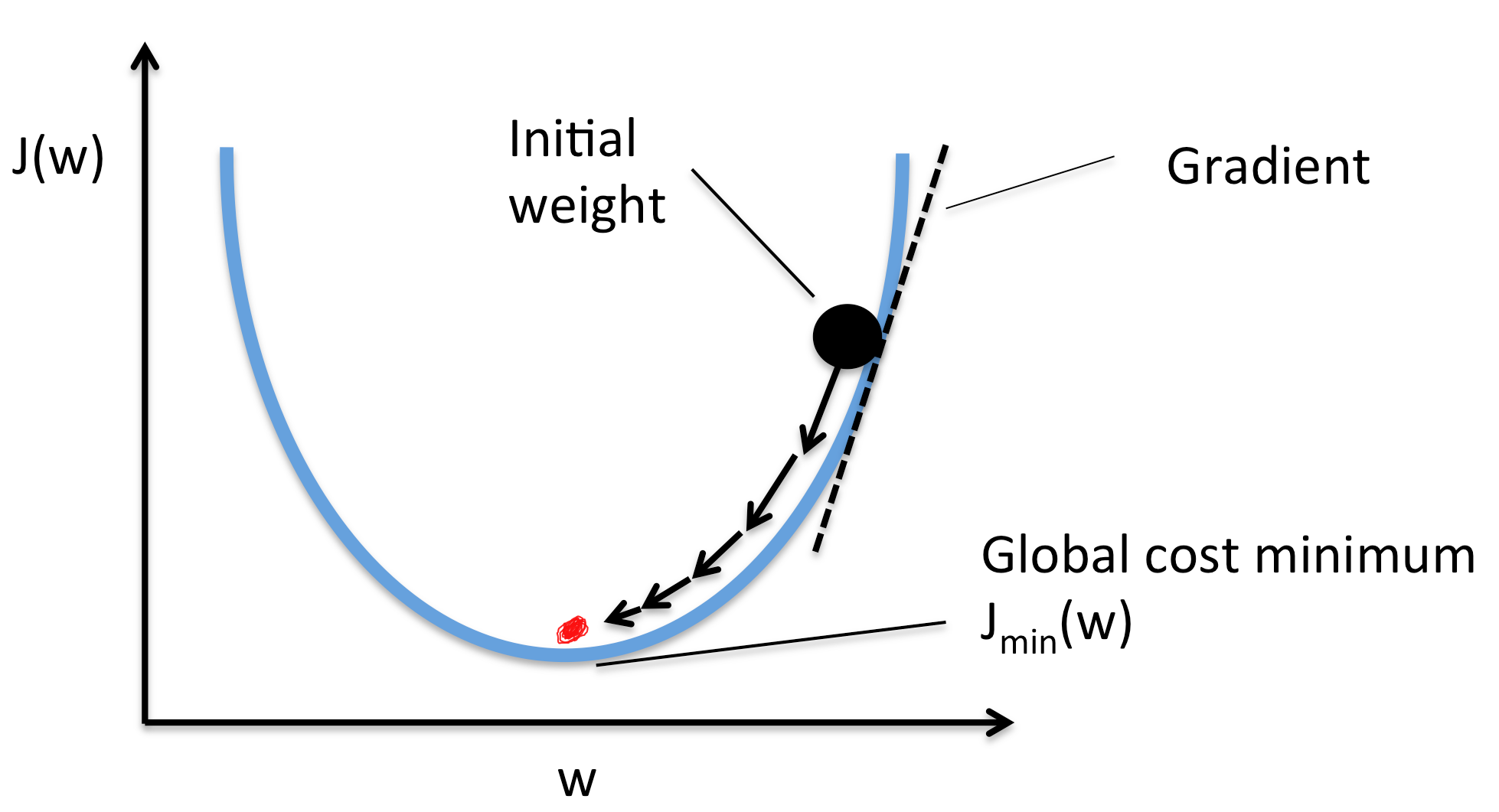 .
.
5. Types of Gradient Descent
-
Stochastic Gradient Descent (SGD) :
the model updates the weights of neurons after calculating the gradient of each single example. So the process will be :
- Take an example
- Feed Forward it to Neural Network
- Calculate its gradient
- Use the gradient we calculated in step 3 to update the weights
- Repeat steps 1–4 for all the examples in the training dataset.
So this type is fast and will be good in huge datasets, but not computationally effective in many cases.
-
Batch Gradient Descent :
On the other hand, Batch Gradient Descent considers all the training examples before updating the weights. it takes the average of the gradients of all the training examples and then uses that mean gradient to update our parameters.
-
Mini-batch Gradient Descent:
It is located in the middle of SGD and Batch Gradient Descent. Neither we use all the dataset all at once nor we use the single example at a time. Mini-batch divide the the training examples into batches, then calculate the average gradient for them. So the process will be :
- Pick a mini-batch
- Feed Forward it to Neural Network
- Calculate the average gradient of the mini-batch
- Use the average gradient we calculated in step 3 to update the parameters
- Repeat steps 1–4 for the mini-batches we created.
So :
Question
Which is the best type of Gradient Descent optimizers ?
Choosing the Gradient Descent optimizer now is very easy in ML Frameworks like TF :
after you build and define your model and its layers, you have to perform Compiler in which you have to introduce your optimizer as an argument:
import tensorflow as tf
model = tf.keras.Model(inputs, outputs)
model.compile(optimizer="SGD",loss="binary_crossentropy")
model.fit(training_data,training_labels)
the above code show selecting SGD optimizer in TF and Keras.
Conclusion :
Like your baby, your model will improve by his trial and failure with your guidance and of course backpropagation and gradient descent are the most important tools for guidance with your baby and your models. In fact they are complementary processes.
