
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes | Coding time: 10 minutes
Bead sort (also called gravity sort) is a natural sorting algorithm. Both digital and analog hardware implementations of bead sort can achieve a sorting time of O(n); however, the implementation of this algorithm tends to be significantly slower in software and can only be used to sort lists of positive integers.
This is a perfect example of an algorithm where the hardware implementation is significantly faster than the software implementation is to contrary to the common belief that software has to be faster than corresponding hardware (think of mechanical calculators)
Gravity sort has been developed by Joshua J. Arulanandham, Cristian S. Calude and Michael J. Dinneen in 2002.
Algorithm
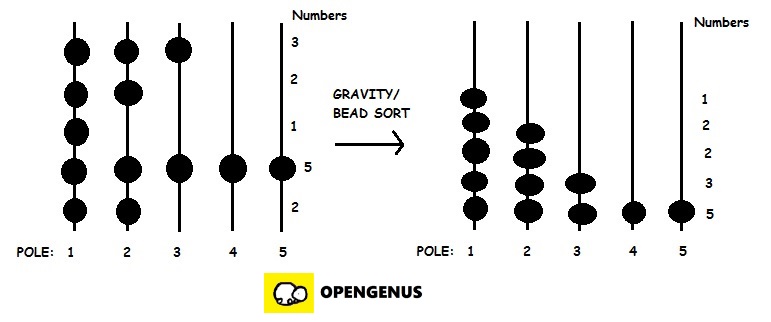
The bead sort operation can be compared to the manner in which beads slide on parallel poles, such as on an abacus. However, each pole may have a distinct number of beads. Initially, it may be helpful to imagine the beads suspended on vertical poles.
In Step 1, put n rows of beads on m vertical poles from left to right, n is the length of the array to be sorted, m is the max num in the array.
Step 2: If we then allow the beads to fall, the rows now represent the same integers in sorted order. Row 1 contains the largest number in the set, while row n contains the smallest.
Why hardware implementation is faster?
This is because sorting step is done by Gravity (a natural physical force) and this step takes place in parrallel in one step.
In software, this step takes a minimum of m clock cycles.
Complexity
Bead sort can be implemented with four general levels of complexity, among others:
-
O(1): The beads are all moved simultaneously in the same time unit, as would be the case with the simple physical example above. This is an abstract complexity, and cannot be implemented in practice.
-
O(√N): In a realistic physical model that uses gravity, the time it takes to let the beads fall is proportional to the square root of the maximum height, which is proportional to n.
-
O(n): The beads are moved one row at a time. This is the case used in the analog and digital hardware solutions.
-
O(S), where S is the sum of the integers in the input set: Each bead is moved individually. This is the case when bead sort is implemented without a mechanism to assist in finding empty spaces below the beads, such as in software implementations.
Implementations
Implementation of Linear search algorithm in 5 languages that includes C, C++, Java, Python and Swift.
- C
- C++
- Java
- Python
- Swift
C
#include <stdio.h>
#include <stdlib.h>
// Part of Cosmos by OpenGenus Foundation
void bead_sort(int *a, int len)
{
int i, j, max, sum;
unsigned char *beads;
# define BEAD(i, j) beads[i * max + j]
for (i = 1, max = a[0]; i < len; i++)
if (a[i] > max) max = a[i];
beads = calloc(1, max * len);
/* mark the beads */
for (i = 0; i < len; i++)
for (j = 0; j < a[i]; j++)
BEAD(i, j) = 1;
for (j = 0; j < max; j++) {
/* count how many beads are on each post */
for (sum = i = 0; i < len; i++) {
sum += BEAD(i, j);
BEAD(i, j) = 0;
}
/* mark bottom sum beads */
for (i = len - sum; i < len; i++) BEAD(i, j) = 1;
}
for (i = 0; i < len; i++) {
for (j = 0; j < max && BEAD(i, j); j++);
a[i] = j;
}
free(beads);
}
int main()
{
int i, x[] = {5, 3, 1, 7, 4, 1, 1, 20};
int len = sizeof(x)/sizeof(x[0]);
bead_sort(x, len);
for (i = 0; i < len; i++)
printf("%d\n", x[i]);
return 0;
}
C++
#include <vector>
#include <iostream>
using namespace std;
#define BEAD(i, j) beads[i * max + j]
// Part of Cosmos by OpenGenus Foundation
// function to perform the above algorithm
void beadSort(vector<int>& a)
{
// Find the maximum element
int max = a[0];
for (size_t i = 1; i < a.size(); ++i)
if (a[i] > max)
max = a[i];
// allocating memory
vector<unsigned char> beads(max * a.size(), 0);
// mark the beads
for (size_t i = 0; i < a.size(); ++i)
for (int j = 0; j < a[i]; ++j)
BEAD(i, j) = 1;
for (int j = 0; j < max; ++j)
{
// count how many beads are on each post
int sum = 0;
for (size_t i=0; i < a.size(); ++i)
{
sum += BEAD(i, j);
BEAD(i, j) = 0;
}
// Move beads down
for (size_t i = a.size() - sum; i < a.size(); ++i)
BEAD(i, j) = 1;
}
// Put sorted values in array using beads
for (size_t i = 0; i < a.size(); ++i)
{
int j;
for (j = 0; j < max && BEAD(i, j); ++j);
a[i] = j;
}
}
// driver function to test the algorithm
int main()
{
vector<int> a{5, 3, 1, 7, 4, 1, 1, 20};
beadSort(a);
cout<<"After Sorting.. "<<endl;
for (size_t i = 0; i < a.size(); ++i)
cout<<a[i]<<" ";
return 0;
}
Java
import java.util.Arrays;
// Part of Cosmos by OpenGenus Foundation
public class BeadSort {
private enum BeadSortStatus {
MARKED,
NOT_MARKED,
}
public static void main(String[] args) {
int[] arrayToSort = new int[]{4, 1, 6, 2, 40, 5, 3, 8, 7};
System.out.println(Arrays.toString(beadSort(arrayToSort)));
}
public static int[] beadSort(int[] arr) {
int max = 0;
for (int anArr : arr) {
if (anArr > max) {
max = anArr;
}
}
//Set up abacus
BeadSortStatus[][] grid = new BeadSortStatus[arr.length][max];
int[] levelcount = new int[max];
for(int i = 0; i < max; i++) {
levelcount[i] = 0;
for(int j = 0; j < arr.length; j++) {
grid[j][i] = BeadSortStatus.NOT_MARKED;
}
}
//Drop the beads
for (int anArr : arr) {
int num = anArr;
for (int j = 0; num > 0; j++, num--) {
grid[levelcount[j]++][j] = BeadSortStatus.MARKED;
}
}
//Count the beads
int[] sorted=new int[arr.length];
for(int i = 0; i < arr.length; i++) {
int putt = 0;
for(int j = 0; j < max && grid[arr.length - 1 - i][j] == BeadSortStatus.MARKED; j++) {
putt++;
}
sorted[i] = putt;
}
return sorted;
}
}
Python
# Part of Cosmos by OpenGenus Foundation
def bead_sort(obj):
if all([type(x) == int and x >= 0 for x in obj]):
ref = [range(x) for x in obj] #for reference
else:
raise ValueError("All elements must be positive integers")
inter = [] #for intermediate
ind = 0 #for index
prev = sum([1 for x in ref if len(x) > ind]) #prev for previous
while prev:
inter.append(range(prev))
ind += 1
prev = sum([1 for x in ref if len(x) > ind])
ind = 0
prev = sum([1 for x in inter if len(x) > ind])
out = []
while prev:
out.append(prev)
ind += 1
prev = sum([1 for x in inter if len(x) > ind])
out = out[::-1]
return out
Swift
/* Part of Cosmos by OpenGenus Foundation */
//
// bead_sort.swift
// Created by DaiPei on 2017/10/12.
//
import Foundation
func beadSort(_ array: inout [Int]) {
let n = array.count
var m = Int.min
// find the max value
for i in 0..<n {
if array[i] > m {
m = array[i]
}
}
var beads = [Int8](repeatElement(0, count: m * n))
// put beads
for i in 0..<n {
for j in 0..<m {
if j < array[i] {
beads[i * m + j] = 1
}
}
}
for j in 0..<m {
// count beads
var sum = 0
for i in 0..<n {
sum += Int(beads[i * m + j])
beads[i * m + j] = 0
}
// move down beads
for i in n - sum..<n {
beads[i * m + j] = 1
}
}
// put sorted value in array using beads
for i in 0..<n {
var j = 0
while j < m {
if beads[i * m + j] == 0 {
break
}
j += 1
}
array[i] = j
}
}
