Home Discussions Write at Opengenus IQ
×

Search anything:

Understanding Bit mask/ Bit map in depth

Binary Tree book by OpenGenus

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Reading time: 25 minutes

Bit manipulation is the act of algorithmically manipulating bits or other pieces of data shorter than a byte.

Now , What is Bit Mask?

A bit mask (or Bitmap) is a data structure, usually an integer or array of bits, that represent a bit pattern which signifies a particular state in a particular computational problem. It takes advantage of bitwise operations.

Example

Consider a situation where you have 5 computers which you assign to your guests. When a new guest arrives or some other event, you need to have information of the computers available or already assigned.

In short, we need the current state of the 5 computers.

There are many ways in which this problem can be represented like:

  • list of computer objects

We will focus on bitmasks.

In the bit mask approach, we will have a 5 bit number where the ith bit conveys information:

  • if ith bit is set to 1, ith computer is occupied
  • if ith bit is set to 0, ith computer is free

Hence, 01101 represents:

  • Computer 2, 3 and 5 are occupied
  • Computer 1 and 4 are free

Why we use bit mask?

We use bit masks because:

  • it is memory efficient in most problems

  • it is computational efficient as we can use bitwise operations which are natively supported by the computer system and will be faster than other operations like addition (+).

Common bit operations

  • Turning on bit:
    [ 0 -> 1 | 1 -> 1 ]

  • Turning off bit:
    [ 1 -> 0 | 0 -> 0 ]

  • Toggle specific bit:
    [ 1 -> 0 | 0 -> 0 ]

  • Querying Bit:
    [ Check whether particular bit is 0 or 1 ]

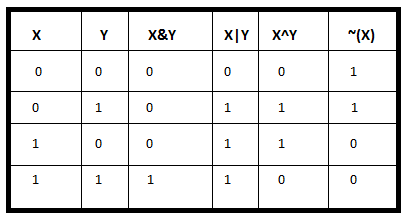
bit Operators :

  • (&) - Bitwise AND
  • (|) - Bitwise OR
  • (^) - Bitwise XOR (Exclusive OR)
  • (!) - Bitwise complement
  • (<<) - Left Shift
  • (>>) - Right Shift

bitwiseOperations

Example :

First Let's take one random number:

178 // base 10 (decimal)
10110010 // base 2 (binary)

data = 178

I will use this number through out the article

1) Quering Bit :

Quering Bit means check particular bit whether it is 0 or 1 at desired position. For that first i have to build a mask.

  • Let's check 3rd bit is 0 or 1
// Build a Mask
mask = 00000100

How? We can have given mask by left shift of 1 by 2 times that is,

mask = 1 << 2
mask = 00000100

Now , AND(&) of data with mask

data    10110010
mask  & 00000100
        ________
ans =   00000000

if(ans is ZERO)
desired bit is zero (0)

if(ans is NON ZERO)
desired bit is one (1)

ans = 0 (base 10)
here, ans is ZERO so, 3rd bit is 0 :)

Why? Here we have used AND(&) operator...
x & 0 = 0
x & 1 = x (x = 0/1)

  • Let's check 5th bit is 0 or 1

Same procedure ,

// Build a mask
mask = 1 << 4
mask = 00010000

// AND(&) of data with mask

data    10110010
mask  & 00010000
        ________
ans =   00010000

ans = 16 (base 10)
here, ans is NON ZERO so, 5th bit is 1 :)

Hack is we are anding(&) by 1 only with our desired bit so if it is 1 then answer will obvious non zero and if it is zero then all bits in answer will be zero.
So , answer (data & mask) is NON_ZERO iff desired bit is set or 1. If answer is zero then desired bit is 0.

2) Turning Bit On :

If we want to set perticular bit to 1 then Bit Mask will help us.

  • Let's set 7th bit to 1
// Build a Mask
mask = 01000000  (7th bit 1 others 0)

// OR(|) of data with mask
data    10110010
mask  | 01000000
        ________
ans =   11110010

Why? Here we have used OR(|) operation

Hack is OR(|) will give ans 0 iff both bits are 0 otherwise it will gives 1

x | 0 = x
x | 1 = 1 (x = 0/1)

Hack is if we do OR(|) of 1 with anything (0/1) it will set ans to 1. So, here we are doing OR(|) operation with our desired bit and it will set that bit to 1. And if We do OR(|) by 0 with any other bit it it will not change that bit.

3) Turning Bit Off :

If we want to set perticular bit to 0 then Bit Mask will help us.

  • Let's set 2nd bit to 0
// Build a Mask
mask = 11111101  (2nd bit 0 others 1)

How? 
mask = ~(1<<2)  [Bitwise complement(~) operator : it will flip all bits ~(11110000) = (00001111)]
mask = !(00000010)
mask = 11111101

// AND(&) of data with mask
data    10110010
mask  | 11111101
        ________
ans =   10110000

Got it?? Because we have used AND(&) :)

Hack is if we do AND(&) of 0 with anything (0/1) it will set ans to 0. So, here we are doing AND(&) operation with our desired bit and it will set that bit to 0. And if We do AND(&) by 0 with any other bit it it will not change that bit.

4) Toggling Bit :

If we want to toggle bits that is 0->1 or 1->0 then Bit Mask will help us.

  • Let's toggle 4 bits [1,2,6,7] of data (10110010)

// Build a Mask
mask = 01100011 (1st , 2nd , 6th , 7th bits are 1 others are 0)

How?

mask = (1<<6) | (1<<5) | (1<<1) | (1<<0)
mask = 01100011

// XOR(^) of data with mask
data    10110010
mask  ^ 01100011
        ________
ans =   11010001

Why? Because we have used XOR(^) operator

Hack is if we do XOR(^) of 0 with anything (0/1) it will not change that bit. So, here we are doing XOR(^) operation with our desired bit and it will put it as it is. And if We do XOR(^) by 1 with any other bit it it will flip that bit.

x ^ 0 = x [0^0 = 0 , 1^0 = 1]
x ^ 1 = ~x [0^1 = 1 , 1^1 = 0] x = {0/1}

Code example

I suggest you go through code it is very simple. I have made function for all above operations. You have to pass data and position of bit on which you want to perform operation.

    #include <bits/stdc++.h> 
    using namespace std; 

    void queryBit(int data , int position){
        int mask,ans;
    
        cout << "Check for " << position << " Bit" << endl;
    
        // storing data
        data = 178;   
        cout << "data  :  " << bitset<8>(data) << endl;

        // Build Mask
        mask = 1 << (position-1);
        cout << "mask  :  " << bitset<8>(mask) << endl;

        // Bitwise AND(&) between data and mask
        ans  = data & mask;  
        cout << "ans   :  " << bitset<8>(ans) << endl;

        if(ans == 0)  // If ZERO then desired bit is 0
            cout << "Bit at position " << position << " is = " << 0 << endl;
        else  // If NON_ZERO then desired bit is 1
            cout << "Bit at position " << position << " is = " << 1 << endl;

        cout << endl;
    }

    void setTo1(int data , int position){
        int mask,ans;

        cout << "Set to 1 at position " << position << endl;

        // storing data
        data = 178;   
        cout << "data  :  " << bitset<8>(data) << endl;

        // Build Mask
        mask = 1 << (position-1);
        cout << "mask  :  " << bitset<8>(mask) << endl;

        // Bitwise OR(|) between data and mask
        ans  = data | mask;  
        cout << "ans   :  " << bitset<8>(ans) << endl;

        cout << endl;
    }

    void setTo0(int data , int position){
        int mask,ans;

        cout << "Set to 0 at position " << position << endl;

        // storing data
        data = 178;   
        cout << "data  :  " << bitset<8>(data) << endl;

        // Build Mask
        mask = ~(1 << (position-1));
        cout << "mask  :  " << bitset<8>(mask) << endl;

        // Bitwise AND(&) between data and mask
        ans  = data & mask;  
        cout << "ans   :  " << bitset<8>(ans) << endl;

        cout << endl;
    }

    void toggleBits(int data , int position){
        int mask,ans;

        cout << "Toggle bit at position " << position << endl;

        // storing data
        data = 178;   
        cout << "data  :  " << bitset<8>(data) << endl;

        // Build Mask
        mask = 1 << (position-1);
        cout << "mask  :  " << bitset<8>(mask) << endl;

        // Bitwise XOR(^) between data and mask
        ans  = data ^ mask;  
        cout << "ans   :  " << bitset<8>(ans) << endl;

        cout << endl;
    }

    int main(){ 

        int data = 178;          // our data - 10110010

        queryBit(data,2);
        queryBit(data,3);

        setTo0(data,2);
        setTo0(data,3);

        setTo1(data,2);
        setTo1(data,3);

        toggleBits(data,2);
        toggleBits(data,3);

        return 0; 
    }

Output:

Check for 2 Bit
data  :  10110010
mask  :  00000010
ans   :  00000010
Bit at position 2 is = 1

Check for 3 Bit
data  :  10110010
mask  :  00000100
ans   :  00000000
Bit at position 3 is = 0

Set to 0 at position 2
data  :  10110010
mask  :  11111101
ans   :  10110000

Set to 0 at position 3
data  :  10110010
mask  :  11111011
ans   :  10110010

Set to 1 at position 2
data  :  10110010
mask  :  00000010
ans   :  10110010

Set to 1 at position 3
data  :  10110010
mask  :  00000100
ans   :  10110110

Toggle bit at position 2
data  :  10110010
mask  :  00000010
ans   :  10110000

Toggle bit at position 3
data  :  10110010
mask  :  00000100
ans   :  10110110

Practical use

  • In programming languages such as C, bit fields are a useful way to pass a set of named boolean arguments to a function.[2]

  • Masks are used with IP addresses in IP ACLs (Access Control Lists) to specify what should be permitted and denied.[2]

  • In computer graphics, when a given image is intended to be placed over a background, the transparent areas can be specified through a binary mask.[2]

—
Understanding Bit mask/ Bit map in depth
Share this