
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will learn about the what is the tree,Binary tree and complete binary tree also how it differs from a general Binary Tree in terms of different operations.
Table of Contents :
- Introduction To Tree Data Structure
- Introduction To Complete Binary Tree
- Complete Binary Tree Terminology :
- Complete Binary Tree Properties
- Algorithm
- Implementation
- Complete Binary Tree Applications
- Introduction To General Binary Tree
- Implementation of General Binary Tree
- Comparision Between General Tree & Complete Binary Tree:
- Quiz
Introduction To Tree Data Structure
The tree is a hierarchical structure that contains a collection of nodes. Where each node presents its value and edges connect them. It also consists of root, parent, child, sibling path, leaf node, etc.
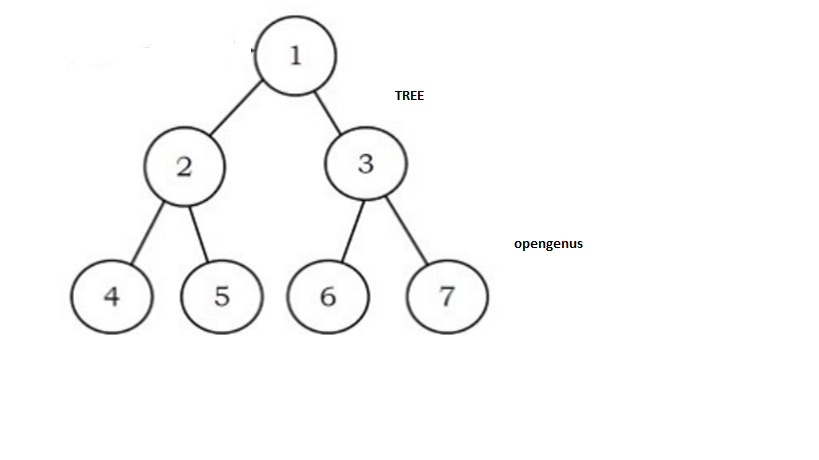
There are different types of trees:
- General tree
- Binary tree
- Binary search tree
- Avl tree
- B-tree
Complete Binary Tree:
A complete binary tree is a binary tree data structure where all level of tree is completely filled by nodes except lowest one.
It is filed from left to right. It contains some similarity of full binary tree, but it is not full binary tree. Cause full binary tree contain zero and two nodes. The last leaf element of tree doesn’t contain right node.
**Binary tree can have in the range of 1 and 2h nodes at the last level h of tree.
**
A perfect tree is always complete binary tree but a complete tree is not perfect tree.
A complete binary tree can be represented using an array.
The number of internal nodes in a complete binary tree of n nodes is [ n/2].
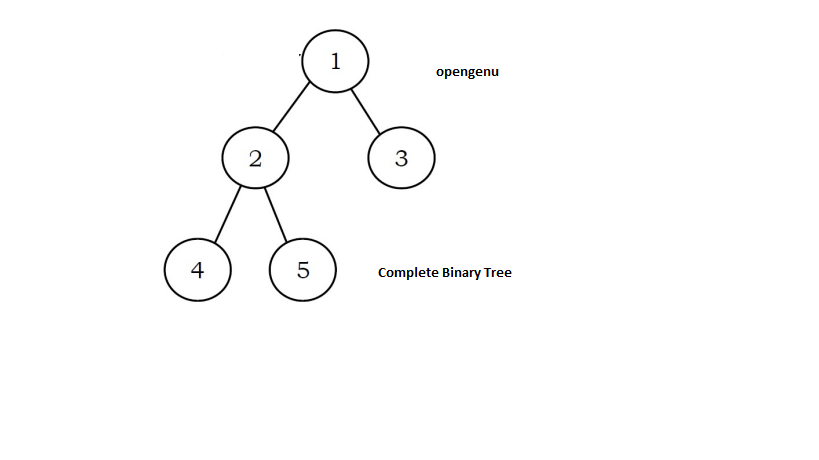
Why complete binary tree has no right sibling?
Before understanding Why complete binary tree has no right sibling let revise some property of tree.
- A complete binary tree has two nodes at each level
- All levels of a tree are filled except the last level.
- All level is filled from left to right direction.
Simplification :
Now let’s try to simplify it. Now consider the level of a tree by L .
If a binary tree is completely filled then at each level tree has 2L nodes.
But it is complete binary tree…Where all the levels of a tree are filled except the last level.So, it doesn’t contain 2L node except last one.
Also, they are they are filed from left to right direction. So, it is not possible for a tree to have a right child node without left child.
** Tree Terminology** :
Root – A special node which dont have any parent node.
Parent :Immedidiate predecessor of node .
Child – Immedidiate successor of node .
Sibling – Nodes with the same parent are sibling.
Path - Number of successive edges from source to destination node .
Degree of a node – Number of children of any node.
Leaf node - node with degree 0 is leaf node.
Height – Number of edges to destination node
Properties
- All leaf node level is n or n-1.
- All level are filled from left to right.
- Last node doesnot hav right sibling.
- Height of the tree is log(n+1).
- All leaves have the same depth.
Algorithm :
Step 1 :Start.
Step 2 :Count the number of nodes.
Step 3 :Set index to 0. Eg .i=0
Step 4 :Set count to 0. Eg .count =0
Step 5 :Start recursion of the binary tree.
Step 6 :if current node is NULL
Return true.
Step 7 :If i>=count
Return false.
Step 8 : Perform recursion for left and right sub tree. And print result.
Step 9: Stop.
Implementation
Code In Python For Complete Binary Tree:
# program to check binary tree is complete binary tree or not
class Node:
def __init__(self, item):
self.item = item
self.left = None
self.right = None
# count nodes
def count_nodes(root):
if root is None:
return 0
return (1 + count_nodes(root.left) + count_nodes(root.right))
# Check if tree is complete binary tree or not
def is_complete(root, index, numberNodes):
# Check tree is empty or not
if root is None:
return True
if index >= numberNodes:
return False
return (is_complete(root.left, 2 * index + 1, numberNodes)
and is_complete(root.right, 2 * index + 2, numberNodes))
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
node_count = count_nodes(root)
index = 0
# check tree is complte or not
if is_complete(root, index, node_count):
print("This tree is complete Binary Tree")
else:
print("This tree is not complete Binary Tree")
Output :
This tree is complete Binary Tree
Explanation:
In this program first count the number of nodes in the binary tree. if it don’t have any node then return 0. and then start recursion of the binary tree from the root . set index (i) to 0 and count to 0.
if the index of current node is under is null, then the tree is a complete binary tree. then return true.
if index of the current node is greater than or equal to the number of nodes in the binary tree then the tree is not a complete binary. and then return false. print the appropite message on user screen.
Applications
- Heap-based data structures
- heap sort.
- Binary Heap
Binary Heap
A Binary Heap is a Binary Tree . It has following properties.
- It is a complete tree .
- All levels are filled except the last level.
- It contain Min Heap or Max Heap.
This property makes heap to be suitable to store in an array.
Array Represenation:
In a Min Binary Heap the key present at root must be minimum among all keys.
A Binary Heap is a Complete Binary Tree. It can represented using as an array also .
- Arr[0] represent is root node .
- Arr[(i-1)/2] represent parent node.
- Arr[(2i)+1] represent left node.
- Arr[(2i)+2] represent right node.
Now lets understand how complete binary tree is differnet of general binary tree.
**General Binary Tree **
A binary tree is a tree data structure where each node of the tree can have a maximum of two children. Where the left node is called the left child and the right node is called the right node. Children of nodes of a binary tree are ordered.
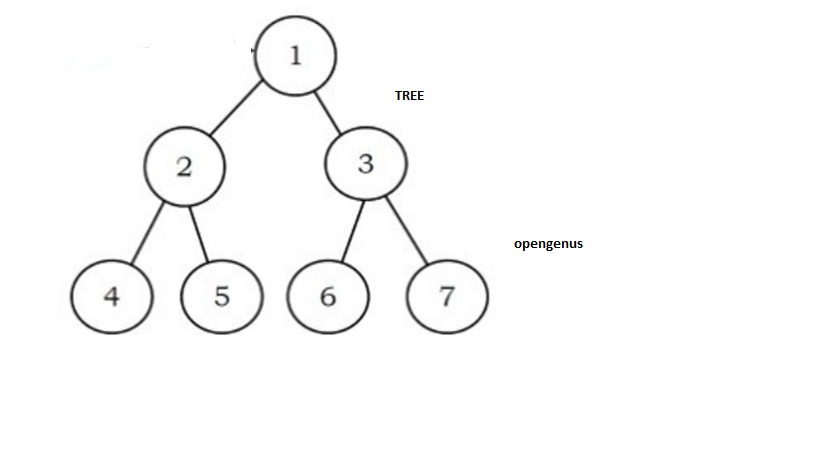
Implementation
Program for General Binary Tree:
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def insert(self, data):
# Compare the new value with the parent node
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the binary tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# insert nodes
root = Node(20)
root.insert(8)
root.insert(4)
root.insert(3)
# Print the binary tree
root.PrintTree()
Output :
3 4 8 20
Explaintaion :
This will insert specific data in to tree.
Comparision Between General Tree and Complete Binary Tree:
| Parameter | General binary tree | Complete binary tree |
|---|---|---|
| Count Of Node | The general tree is a tree in which each node can have two children or nodes. | A complete binary tree is a binary tree data structure where all level of the tree is filled by nodes except the lowest one. |
| Tree representation | Tree representation is easy. | Tree representation somewhere is easy |
| last level of tree | In a general binary tree, a node in the last level can have two children. | A complete binary tree node in the last level can have any child which is present on the left side. |
| Order of nodes | There is no order for nodes. | In a complete binary tree, the node should be filled from the left to right. |
| Naming Convention | A general binary tree is also known as a binary tree. | A complete binary tree is also known as an almost complete binary tree. |
| Limitation | A binary tree can’t have more than two child nodes. | A binary tree can’t have more than one child node. |
| Degree of a Node | The degree of a node is 2 | The degree of a node is 1 |
| Subtree | While in a binary tree, there are mainly two subtrees: left-node and right-node. | While in a binary tree, there are mainly two subtrees: left-node. |
| Node Position | All the nodes lean towards the left and right. | All the nodes lean towards only one side. left side. |
| Application | Decision tree , Expression evaluation and Sorting. | Heap-based , data structures , heap sort |
