Cycle in a graph using degree of nodes of the graph

There are different ways of detecting cycle in a graph. Let us understand how to detect cycles in an undirected graph using the degree of each vertex.

Introduction

Our objective is to check if a cycle exists in an undirected graph. What is a cycle ? A graph that has a number of vertices connected in a close chain, is said to contain a cycle or a loop.
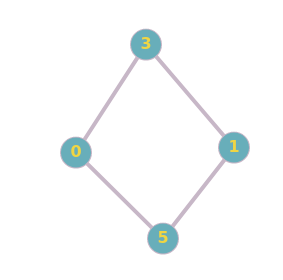
Look at the graph below :

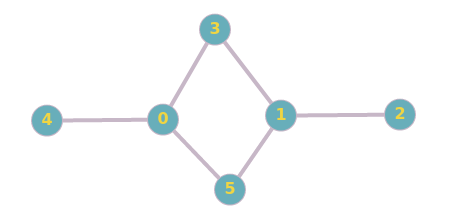
Fig. 1

There is a cycle formed by the nodes 0,3,1 and 5.

NOTE : Self loops are also considered as a cycle in the graph. Take a look at this graph

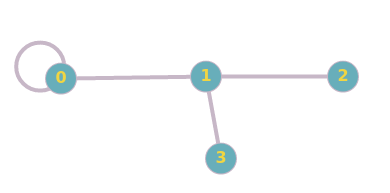
Fig 2.

The vertex 0 forms the cycle in this undirected graph.

Fig 3.

What is degree of a vertex ? The degree of a given vertex is the number of edges that are incident to that vertex.

Intuition

Do you notice something about the vertices that do not form a cycle in the graph ?
The vertices that have a degree of 1 can never be part of a cycle. For a vertex to be part of a cycle, it needs to have a degree of atleast 2, that is, the vertex should be connected to more than 1 vertex. To find the nodes forming the cycle, eliminate all nodes with degree 1, until only the nodes with degree 2 remain. These are the nodes that will form the cycle.
This inituition is the underlying logic that we are going to apply to detect cycle and the vertices forming the cycle.

Algorithm

1. Create a map storing each vertex and its corresponding degree
2. Create a queue containing only the vertices whose degree is 1
3. Maintain a visited array and update it when any vertex is visited
4. For all nodes in the queue, visit all their adjacent vertices of the elements and decrement their degree by 1 (Simulating the vertex with degree 1, being removed), until queue becomes empty.
5. Keep updating the queue, with unvisited vertices of degree 1
6. Once the queue is empty, check if all vertices of the graph have been visited
   • If yes, there is no cycle in the graph
   • If not all vertices are visited, there is a cycle in the graph. Print the nodes that are unvisited. These nodes form the cycle

Tracing the algorithm

Let us consider the first graph as input

The adjacency list/map for the above graph is :

0 -> 1, 3, 4
1 -> 2, 3, 5
2 -> 1
3 -> 0, 1
4 -> 0

Step 1 : Create a map of vertices and corresponding degree
Here is the map :

0 -> 3
1 -> 3
2 -> 1
3 -> 2
4 -> 1

Step 2 : Create a queue with all nodes with degree 1
Look at the map and add vertices from the map that have degree as 1
Initially, the queue is :

[2 , 4]

We need to keep updating this queue

Step 3 : Create a boolean visited array, keeping track of vertices that are visited. Initially no vertex is visited.

[false, false, false, false, false, false]

Step 4 :
The queue is :
[2 , 4]
Pop front element from queue, and decrement degree of all its adjacent vertices. Mark the front element of queue as visited.
(2 is popped)
Updated queue : [4]
Mark vertex 2 as visited
Updated visited array :
[false, false, true, false, false, false]
Decrement degree for 2's adjacent node. 2 is connected to 1. Hence decrement degree of node 1.
Updated map :
0 -> 3
1 -> 2
2 -> 1
3 -> 2
4 -> 1

Since node 2 is technically removed, new graph is :

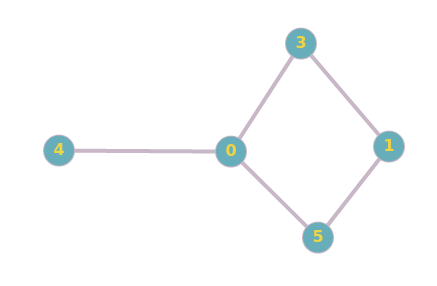
queue is still not empty. Repeat Step 4.
Pop front element form queue and decrement degree of all its adjacent vertices. Mark the front element of queue as visited.
Updated queue : []
Mark vertex 4 as visited
Updated visited array :
[false, false, true, false, true, false]
Decrement degree for 4's adjacent node. 4 is connected to 0. Hence decrement degree of node 0.
Updated map :
0 -> 2
1 -> 2
2 -> 1
3 -> 2
4 -> 1

Since node 4 is technically removed, new graph is :

queue is now empty. Goto Step 5.

Step 5 : Keep updating the queue, with unvisited vertices of degree 1
Take a look at our map
0 -> 2
1 -> 2
2 -> 1
3 -> 2
4 -> 1

There are no other vertices with degree 1 that are unvisited.
NOTE : Vertex 2 and 4 have degree 1, but are visited. Since there are no other vertices that can be added to the queue, we do not update the queue.

Step 6 : Once the queue is empty, check if all vertices of the graph have been visited.
Currently the queue is : []
Our visited array is : [false, false, true, false, true, false]
If the entire array is true ( all vertices were visited) then there is no cycle. But Vertices 0, 1, 3, and 5 have not been visited, and they form the cycle in the graph.
Output : Cycle exists. Nodes 0, 1, 3, 5 form the cycle

Takeaways

Still don't get the big picture ?
Hint 1 : A vertex with degree 1 can never be part of a cycle
Hint 2 : Every graph in which each vertex has degree atleast 2 must contain a cycle

What we are essentially doing in the algorithm is, keep removing the vertices with degree 1 and keep reducing the graph. If we are left with a graph with all vertices having degree >=2, the graph contains a cycle.

Implementation in C++

//Detect cycle in a graph using Degree of graph
#include<iostream>
#include<cstdlib>
#include<vector>
#include<map>
#include<unordered_map>
#include<queue>
using namespace std;

class graph{
    private : map<int,vector<int>> adjList;
              int n,e; //no of vertices and edges
    public : void detect_cycle();
             void input();
};

void graph::input(){
    cout<<"Enter the number of vertices : \n";
    cin>>n;
    cout<<"Enter the number of edges : \n";
    cin>>e;
    cout<<"Enter the adj list for the undirected graph \n";
    for(int i=0;i<e;i++){
        int start,end;
        cin>>start;
        cin>>end;
        adjList[start].push_back(end);
        adjList[end].push_back(start);
    }
    //print adj list
    cout<<"The adj list is :\n";
    for(auto &val : adjList){
        cout<<val.first<<" : ";
        for(int el : val.second){
            cout<<el<<" ";
        }
        cout<<"\n";
    }
}

void graph::detect_cycle(){
    unordered_map<int,int> deg;
    for(int i=0;i<n;i++){
        deg[i]=adjList[i].size();
    }
    bool visited[n];
    for(int i=0;i<n;i++)
        visited[i]=false;
    queue<int> q;
    while(1){
        //pushing all degree 1 nodes into the queue
        //recursively updating the nodes with degree 1
        for(auto &val : deg){
            //To make sure an already visited vertex is not pushed again to the queue
            if(val.second==1 && visited[val.first]==false)
                q.push(val.first);
        }

        if(q.empty()) break;

        while(!q.empty()){
            int temp = q.front(); 
            q.pop();
            visited[temp]=true;
            //deleting node with degree 1
            for(int i=0;i<adjList[temp].size();i++){
                deg[adjList[temp][i]]--;
            }

        }
    }
    int f=0;
    for(int i=0;i<n;i++){
        if(visited[i]==false)
            f=1;
    }
    if(f==0)
        cout<<"No cycle detected !\n";

    else{
        cout<<"Cycle detected at :\n";
        for(int i=0;i<n;i++){
            if(visited[i]==false)
                cout<<i<<" ";
        }
    }
    
}

int main(){
    graph g;
    g.input();
    g.detect_cycle();
    return 0;
}

Output

The adj list is :
0 : 4 3 5 
1 : 3 5 2 
2 : 1 
3 : 0 1 
4 : 0 
5 : 0 1 
Cycle detected at :  
0 1 3 5

Explanation

Let's take a closer look at the detect_cycle() function.

• We use an unordered map to store the vertices with their degree. The degree of each vertex is the size of its corresponsing value of the adjacency map.
• Next, we initialize the boolean visited array to false, since no vertex has been visited yet.
• Then the queue is updated with vertices with degree 1. We do this to remove these vertices, since they do not have to potential to form a cycle. But these vertices entries are still present in the adjacency list as well as the unordered_map deg. Then, where are these vertices with degree 1, removed ? We simulate the removal of these vertices, by decrementing the degree of all the adjacent nodes of these vertices, indirectly removing these vertices.
• Once the queue becomes empty, we keep checking again, for any new vertices (unvisited) with degree 1. If so, we update the queue with these vertices, and continue the same process of their removal, by decrementing these vertices' adjacent node degrees.
• At the end, after the queue finally becomes empty, and we are unable to find any more vertices with degree 1, we check the visited array to see if all vertices have been visited.
  • If a vertex has not been visited at the end of this while() loop (after removing all degree 1 vertices), it means that its degree is atleast 2 (if degree was 1, that vertex would have been visited). According to Hint 2, all such vertices form a cycle.
• We print the nodes which have not been visited (nodes that have degree >= 2) as the nodes forming the cycle in the graph.
• If all vertices have been visited, there is no cycle in the graph.