Detect Cycle in Undirected Graph using Union Find algorithm

In this article, we've explored the approach to detect a cycle in undirected graph using union-find algorithm. This takes O(VE) Time Complexity.

Table of Contents
1)Glance of Union-Find algorithm
2)Introduction
3)Algorithm to find cycle using Union-Find
4)Understanding algorithm through example
5)Implementation in Python
6)Conclusion

1)Glance of Union-Find algorithm

Disjoint-Set is the data structure used in case of Union-Find algorithm.

Disjoint-Set is defined as follows:

Given a set of elements. These items are partitioned into several subsets such that each element is restricted to a particular subset.

In simple terms, A Disjoint-Set data structure is a group of sets where no two sets contain the same element.

It is also called union-find data structure because it supports Union and Find operations on subsets.Let's understand those terms..

Find: Each subset is represented by an element of that subset known as the set-representative.This operation returns the set-representative of a particular element to which it belongs to. This operation has worst case time complexity of O(N) where N is the number of elements in the set since it finds the set-representative recursively.

Union:In this operation two subsets are merged into one subset.The set-representative of the merged subset will one among the set-representatives of those subsets which are merged. This operation has time complexity of O(1).

There is one more operation called make-set operation.

Make-Set:This operation creates disjoint sets for each element in the given set.Intially set-representative for each disjoint set will be the element contained in it. This operation has time complexity of O(1).

Here each subset can be called as a disjoint-set.

2)Introduction

In simple terms, a graph is said to have cycle if there exists a path whose start vertex and end vertex are the same.It is termed as cyclic graph.

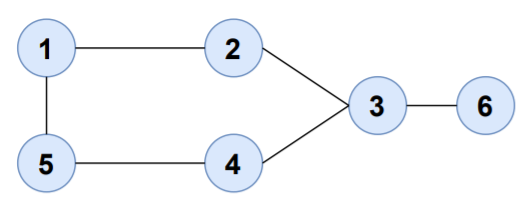
Consider the path,

1-2-3-4-5-1

The start and end vertices are the same.Hence, the graph contains cycle.

3)Algorithm to find cycle using Union-Find

1)Create disjoint-sets for each of the vertices in the graph.
2)Repeat the following steps for each edge(u,v) in the graph
-If u and v both belong to the same disjoint-set then cycle exists in the graph.
-Else merge the disjoint-sets in which u and v are present.

4)Understanding algorithm through example

Let's use the Union-Find algorithm to find cycle in an undirected graph.

Find the edges from the graph.

1-2
2-3
3-4
3-6
4-5
1-5

As there are six vertices, we'll create six disjoint-sets.

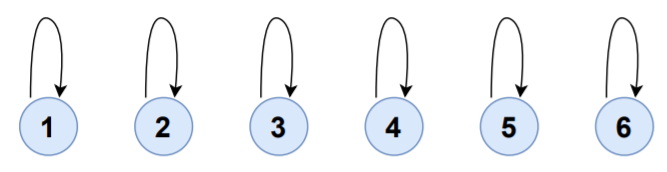
SET	ELEMENTS	SET-REPRESENTATIVE
S1	{1}	1
S2	{2}	2
S3	{3}	3
S4	{4}	4
S5	{5}	5
S6	{6}	6

Consider the edge 1-2,

FIND(1)=1
FIND(2)=2

UNION(1,2)

S1,S2 will be merged to S1 and set-representative of S1 will now be 1.

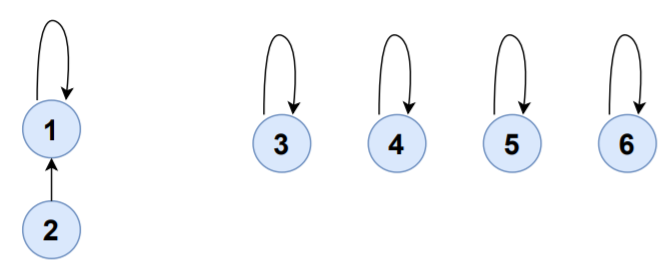
SET	ELEMENTS	SET-REPRESENTATIVE
S1	{1,2}	1
S3	{3}	3
S4	{4}	4
S5	{5}	5
S6	{6}	6

Consider the edge 2-3,

FIND(2)=1
FIND(3)=3

UNION(1,3)

S1,S3 will be merged to S1 and set-representative of S1 will now be 1.

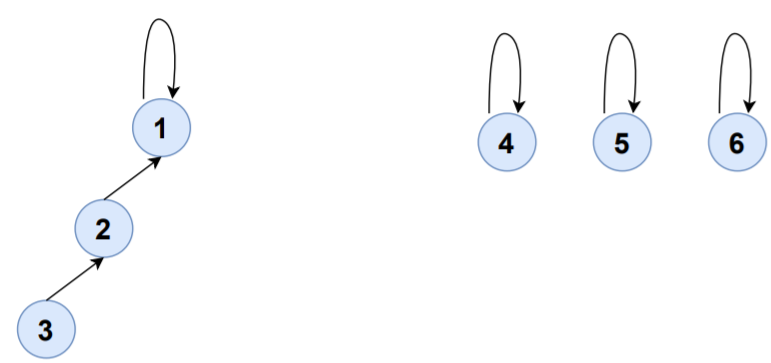
SET	ELEMENTS	SET-REPRESENTATIVE
S1	{1,2,3}	1
S4	{4}	4
S5	{5}	5
S6	{6}	6

Consider the edge 3-4,

FIND(3)=1
FIND(4)=4

UNION(1,4)

S1,S4 will be merged to S1 and set-representative of S1 will now be 1.

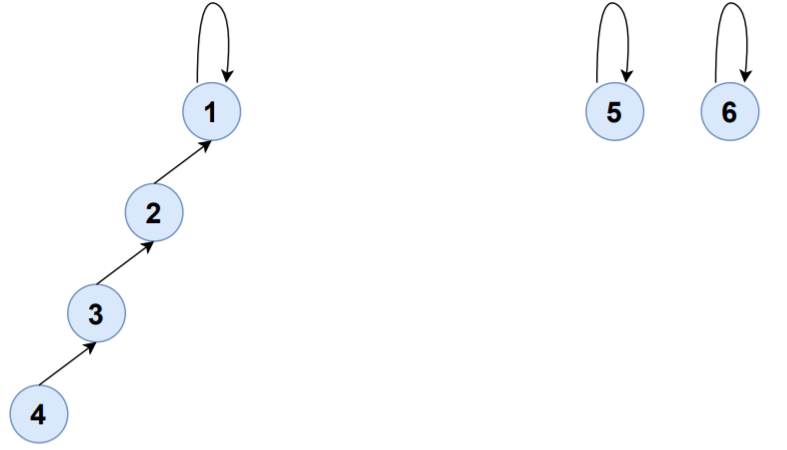
SET	ELEMENTS	SET-REPRESENTATIVE
S1	{1,2,3,4}	1
S5	{5}	5
S6	{6}	6

Consider the edge 3-6,

FIND(3)=1
FIND(6)=6

UNION(1,6)

S1,S6 will be merged to S1 and set-representative of S1 will now be 1.

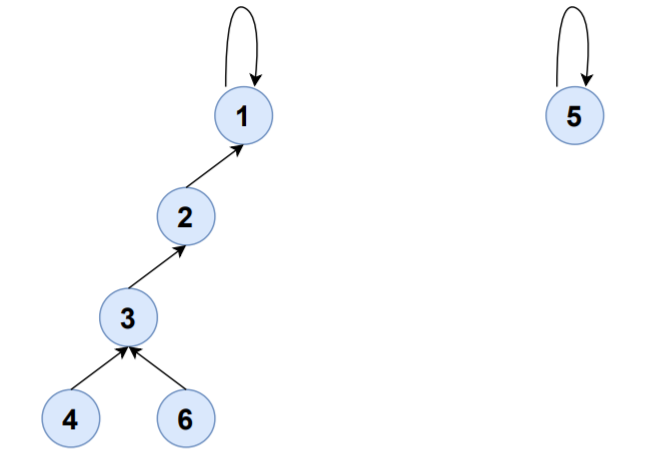
SET	ELEMENTS	SET-REPRESENTATIVE
S1	{1,2,3,4,6}	1
S5	{5}	5

Consider the edge 4-5,

FIND(4)=1
FIND(5)=5

CALL UNION(1,5)

S1,S5 will be merged to S1 and set-representative of S1 will now be 1.

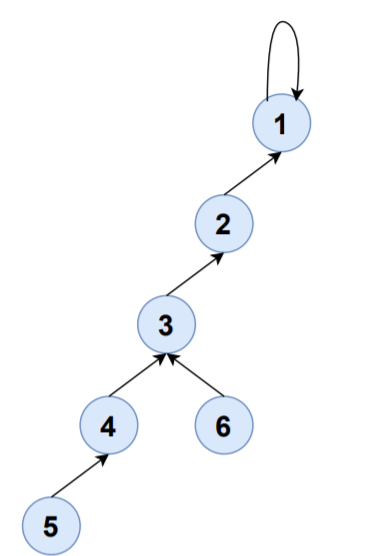
SET	ELEMENTS	SET-REPRESENTATIVE
S1	{1,2,3,4,5,6}	1

Consider the edge 1-5,

FIND(1)=1
FIND(5)=1

Here FIND(1)=FIND(5) that means both belong to same disjoint set. Hence,the graph has a cycle.

5)Implementation in Python

class Union_Find:
    def make_set(self,n):
        self.disjoint_set={vertex:vertex for vertex in range(1,n+1)}#Initializing n subsets and make contained vertex itself the set-representative for each subset
    def find(self,vertex):
        if self.disjoint_set[vertex]==vertex:#A set-representative can be found if v:v
            return vertex
        return self.find(self.disjoint_set[vertex])
    def union(self,x,y):
        set_representative_X=self.find(x)#find set-representative of x
        set_representative_Y=self.find(y)#find set-representative of y
        self.disjoint_set[set_representative_Y]=set_representative_X#make set-representative of y as x

def isCyclic(edges,no_of_vertices):
    ds=Union_Find()
    ds.make_set(no_of_vertices)
    for x,y in edges:
        if ds.find(x)==ds.find(y):#if set-representatives of both the vertices are the same then cycle exists
            print("Cycle exists in the graph!")
            return
        ds.union(x,y)#merge subsets x and y
    print("Cycle doesn't exist in the graph!")
V=int(input())
E=int(input())
edges=[]
for t in range(E):
    x,y=[int(x) for x in input().split()]
    edges.append([x,y])
isCyclic(edges,V)

Input:

V=6
E=6
edges=[[1,2],[2,3],[3,4],[3,6],[4,5],[1,5]]

Output:

Cycle exists in the graph!

Consider the graph which does not contain a cycle..

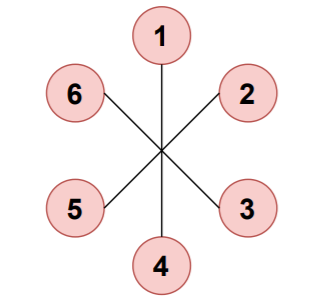
Input:

V=6
E=6
edges=[[1,4],[2,5],[3,6]]

Output:

Cycle doesn't exist in the graph!

6)Conclusion

The time complexity of Union-Find algorithm is O(V), where V is the number of vertices in the graph, in the worst case .

As we need to visit each edge it takes time of O(E) where E is the number of edges in the graph.

Hence, the overall time complexity of detecting cycle in Undirected Graph using Union-Find is O(VE).

In this case, V is number of vertices and E is number of edges. In case of a dense graph, E is of the order of O(V²). So, in a dense graph, this approach takes O(V³) Time Complexity.

With this article at OpenGenus, you must have the complete idea of how to Detect Cycle in Undirected Graph using Union Find algorithm.