
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 10 minutes
In this article, we have explained the differences between Directed and Undirected Graphs based on different attributes such as adjacency matrix, entropy and much more.
Before we start with the problem at hand we should first recall what graphs are.
Graphs are non linear data structure that enables us to viusalise structure of objects connected using links. Thre are two main components of a graph namely-
- Nodes - The vertices that represent objects.
- Edges - The lines that show relationship between the objects
This is a general definition. The exact thing that nodes and edges represent depends on what we are using our graph to represent. For example, If we model followers on Instagram, Nodes will represent accounts, and edges will depict "x" following "y." Or, if we model a computer network, Nodes will represent computers and edges the connection between them.
There are 2 Types of graphs on basis of direction of edges
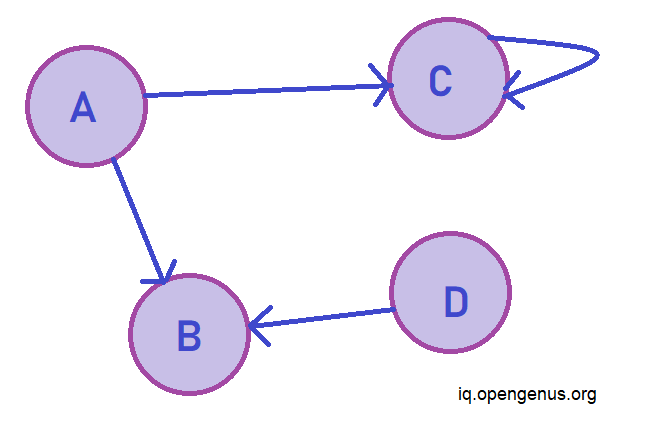
- Directed graphs - The edges are orderedd pair ie.(u,v) and (v,u) have different meaning where (u,v) is read as edge from u to v. Hence there is set direction where information can flow. This direction is represented by arraows used as edges. The following graph can only be traversed from A to B
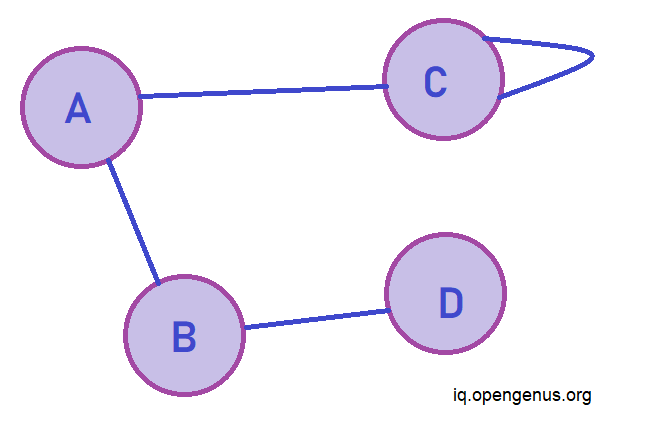
- Undirected graph - The edges are unordered pair. Hence, (u,v) and (v,u) mean the same thing . The flow of information is in both directions simultaneously. Since there is no set direction undirected arcs represent edges. The following graph can be traversed from A to B as well as from B to A.
Now, we will further discover the differences between these two graphs
Edges
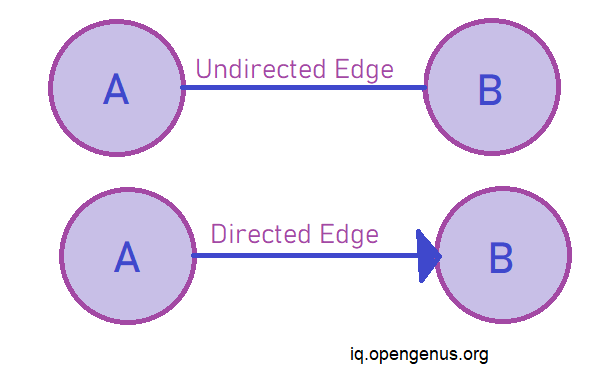
In undirected graphs the edges are bidirectional, with no direction associalted with them the absence of arraow differenciates them from directed graphs. In directed graphs since the edges can only be traversed in only 1 direction in pictoral depiction arrows are used as eedges in directed graphs with arrow head pointing to Endpoint of relationship.
Nodes
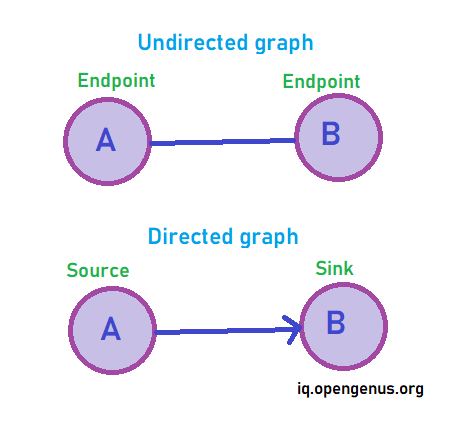
Even though the pictorial representation of the graphs usually do not change whether it be undirected or directed graph but, the directed graph has concept of source and sink vertices. Wherein the node from which the edge orignates is called source vertex while the node at which the edge terminates is known as sink vertex. while in undirected graphs since the arcs are bidirectional the two nodes joined by edges are simply known as end points.
Adjacency Matrix
Since the edges in undirected graph are bi-directional it leads to formation of of an adjacency matrix that is symmetrical.
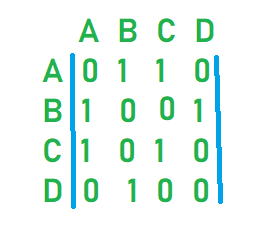
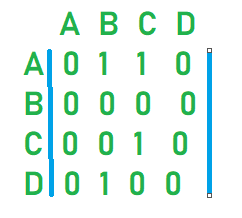
However in case of directed graphs no such symmetry is seen hence it is a usre way of knowing that if adjacency matrix is not symmetrical it will be a directed graph.
== Symmetrical directed graphs are undirected graphs.==
Entropy
In physical sciences entropy is a measure of disorder of a system. Similarly in in graph theory entropy is the index for describing the structure and function of a network. Entropy is related to amount of information stored in a graph. This is used in field of computer science to check compression of data as compressed data is more random and hence has higher entropy.
Compared to a directed network an undirected network has higher entropy for lower number of edges and this trend changes as number of edges increases. Entropy is mainly dependent on number of edges and directed networks are again a special case due to the asymmetric transfer.
The directed and undirected graphs also differ in the methods that their entropy is calculated.For an undirected graph we use the method given by Körner where
Entropy of graph H(G) = min(I(X,Y))
where X is uniform random vertex in G and Y is independent set containing X.
However for directed graphs we use Chung's generalisation or von Neuman approach which is based on graph laplacian , this can be applied to both weakly and strongly directed graphs a simple form of this be represented in simple node in-degree out-degree based statistics.
Applications
Since both directed and undirected graphs differ so much it is natural that they differ in their functionality.
Undirected graphs are more restrictive than directive graphs as they do not allow for modelling of realtionships.
The most common use of undirected graph is to represent network topologies in the field of computer networksand can also be used to represent pedestrian pathways where foot traffic is allowed in both directions between an intersection.
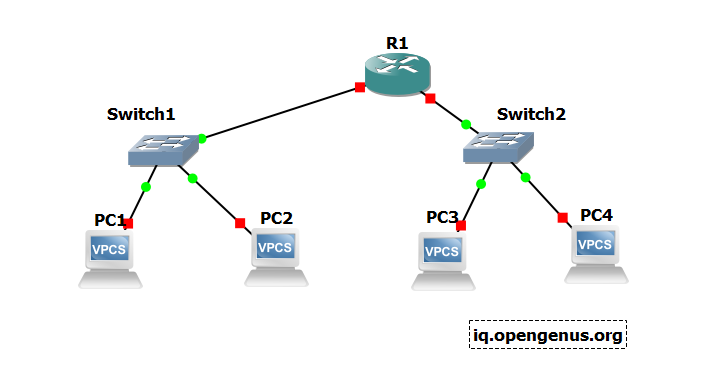
In the above example the componenets inthe network can be thought of as nodes and the connection between them as edges.
Trees are connected acyclic graphs we have read this over and over this means that we should be able to traverse from any node v to any node u. If we take trees to be directed then it may not be possible to traverse to a node from any other node. Unless qualified otherwise(phylogenic and family trees) trees are usually taken to be undirected.
Directed graphs however are useful for modelling real world structures. Usually used for phylogenic trees as they contain parent child relationship the arrow usually points towards the child. This is helpful as undirected graph would fail at distinguishing between the parent and the child.
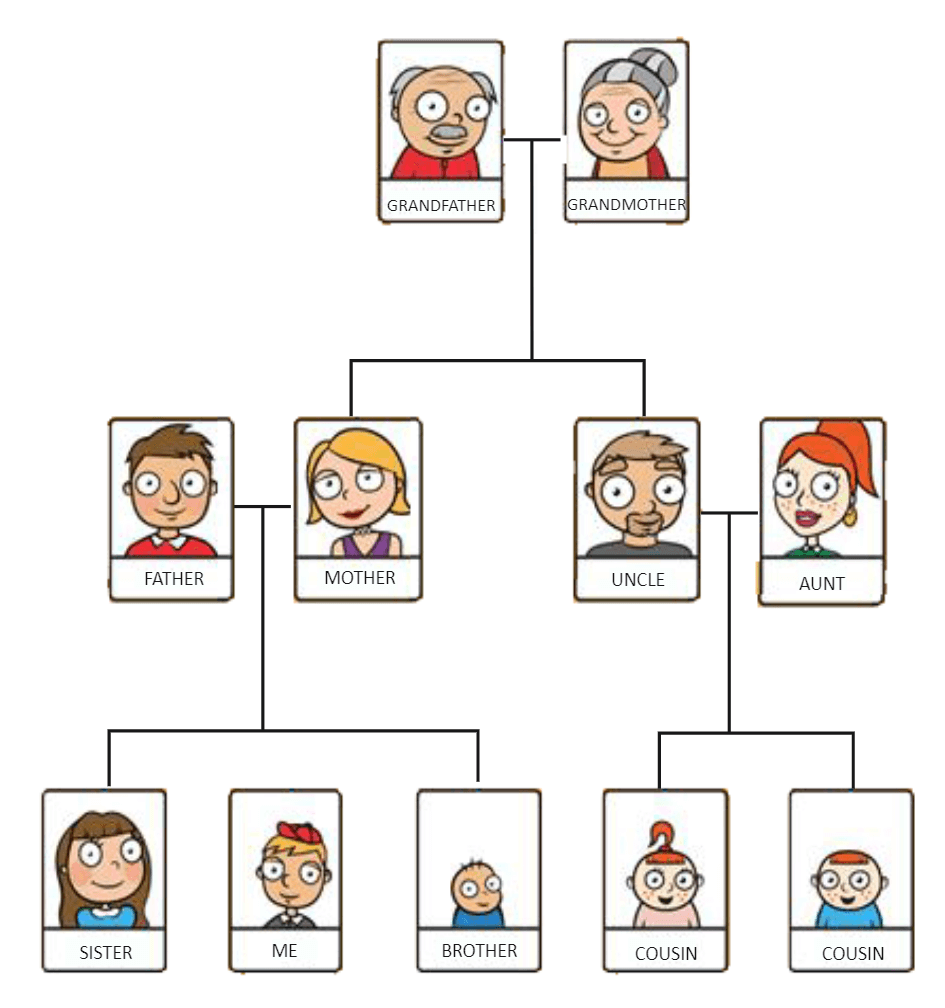
This can be modelled as directed graph with people as nodes and arrows from parent to child.
Summary
| Title | Undirected Graph | Directed Graph |
|---|---|---|
| Edges | In an undirected graph the edges are bi-directional and represented by line segment |
In an directed graph the edges are unidirectional and are depicted by a ray |
| Node | In an undirected graph there is no concept of source and sink they are only endpoints |
In a directed graph the node at which the edge orignates is called source and one which it terminates on is called sink |
| Adjacency Matrix | Undirected graph forms a symmetric matrix since edges are bi-directional |
Directed graphs form asymmetric matrix as edges are unidirectional |
| Applications | Undirected graphs to model those situations where rather than parent-child relation there exists a simple transactory relationship betweeen objects |
Directed graphs are used to model thode situations where we can see a clear parent child relationship |
| Entropy | Undirected graphs has higher entropy for lower number of edges and it's entropy is calculated using Shanons method |
Directed graphs have higher entropy for higher number of edges and to calculate its entropy we use von Neumann approach |
