An Euler path is a path that uses every edge of the graph exactly once. Edges cannot be repeated. This is an important concept in designing real life solutions. In this article, we have explored the basic ideas/ terminologies to understand Euler Path and related algorithms like Fleury's Algorithm and Hierholzer's algorithm.

Basic terminologies and ideas we explored are:

• Walks
• Trails, Closed trails, Circuits
• Path, Cycle
• Euler path and Euler circuit
• Euler's theorem and properties of Euler path
• Algorithms:
  • Fleury’s Algorithm
  • Hierholzer's algorithm

Walks

If we simply traverse through a graph then it is called as a walk.There is no bound on travelling to any of the vertices or edges for ny number of times.

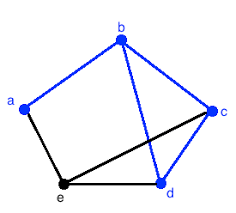
here a walk can be:

a->b->d->c->b

Trails

Now if we restrict a walk such that we visit each edge of the walk only once is called a Trail.

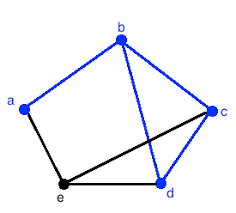
in the above diagram a valid Trail would be:

a->b->c->d->b

Closed trail/ Circuit

A closed trail happens when the starting vertex is the ending vertex.

A closed trail is also known as a circuit.

Path

If we further restrict the vertex repeat of a trail, then we get a path i.e. Vertex cant be repeated.

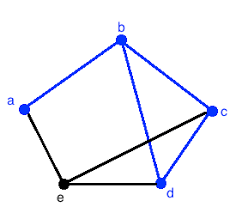
a->b->c->d
is a path.

Cycle

A closed path is also called as a cycle. Here the path shall have the same starting and ending point.

Now paths are what we further want to study.

Paths can be again peeled into Hamiltonian and Euler path w.r.t graph theory.

Of these two we tend to talk about Euler path.

Euler path and circuit

An Euler path is a path that uses every edge of the graph exactly once. Edges cannot be repeated. This is not same as the complete graph as it needs to be a path that is an Euler path must be traversed linearly without recursion/ pending paths.

This is an important concept in Graph theory that appears frequently in real life problems. Think and realize this path.

An Euler circuit is same as the circuit that is an Euler Path that starts and ends at the same vertex.

Euler's Theorem

A valid graph/multi-graph with at least two vertices shall contain euler circuit only if each of the vertices has even degree.

Now this theorem is pretty intuitive,because along with the interior elements being connected to at least two, the first and last nodes shall also be chained so forming a circuit.

A valid graph/multi-graph with at least two vertices has an Euler path but not an Euler circuit if and only if it has exactly two vertices of odd degree.

Properties of Euler paths/ circuits

Eulerian path for undirected graphs:

1. We must understand that if a graph contains an eulerian cycle then it's a eulerian graph, and if it contains an euler path only then it is called semi-euler graph.

2. All the vertices with non zero degree's are connected.

3. If the no of vertices having odd degree are even and others have even degree then the graph has a euler path.

Eulerian path for directed graphs:

To check the Euler nature of the graph, we must check on some conditions:

1. All the nodes must be connected.
2. The nodes/vertices must have same in-degree and out-degree.

in-degree: The no of incoming connections to a vertex.

out-degree: The no of out going connections from each vertex.

After such analysis of euler path, we shall move to construction of euler trails and circuits.

Construction of euler circuits

Fleury’s Algorithm (for undirected graphs specificaly)

This algorithm is used to find the euler circuit/path in a graph.

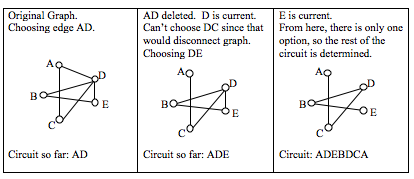
1. check that the graph has either 0 or 2 odd degree vertices.

2. If there are 0 odd vertices, start anywhere. If there are 2 odd vertices start any one of them.

3. Next you have to trace the edges and delete the ones you just traced,if anywhere you get a bridged and a non bridged , choose the non bridged.

4. Stop when you run out of edges.

for example:

complexity analysis:
The fleury's algorithm takes about O(E * E) time.

Hierholzer's algorithm (for directed graphs specifically)

This algorithm may be confusing at first, but it isn't.
1.Here we just have to start at a vertex v, then trace the connected vertices and we will see that we get stuck at the v vertex only, once we are stuck we add the 'v' vertex to the circuit and then back track to the previous nearest vertex.The path we trace is added o the path list.When we are stuck that means the vertex doesn't have any unused edge.

lets look at an example:

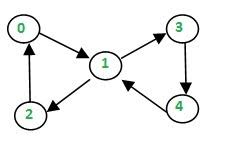
we start with the '0' vertex.we travel to '1'. our path is hence
path={o,1}.
so we delete the edge between '0' and '1'.Then we travel from '1' to '2' then to '1'. so after all these the path would be={0,1,2}
the graph would look as such:

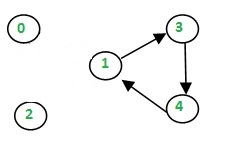
Now we are stuck in '0' so we backtrack and add '0' to the circuit.
circuit={0}.
Then we go back to '2' and stuck here as well so circuit ={0,2}
Then '1' , but it has unused edges so we move forward in our path.
we repeat the same for 1->3->4->1, now we are stuck here, so we backtrack and add 1 to the circuit={0,2,1}.
Finally we've circuit = {0,2,1,4,3,1,0}.

The algorithm takes linear time O(|E|).

Graphs

A connection of nodes through edges is called graph.Graphs can be further Directed and Undirected.

well the fundamentals of graph theory in relation to Euler Path ends here.

Happy coding.