Reading time: 40 minutes

The Hopcroft–Karp algorithm is an algorithm that takes as input a bipartite graph and produces as output a maximum cardinality matching, it runs in O(E√V) time in worst case. Let us define few terms before we discuss the algorithm.

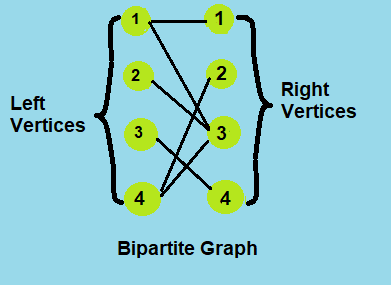
Bipartite graph

A bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

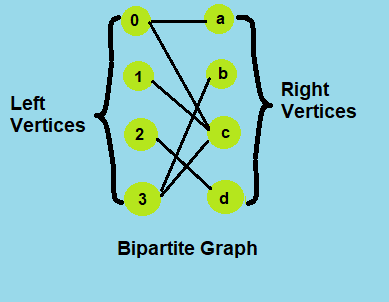
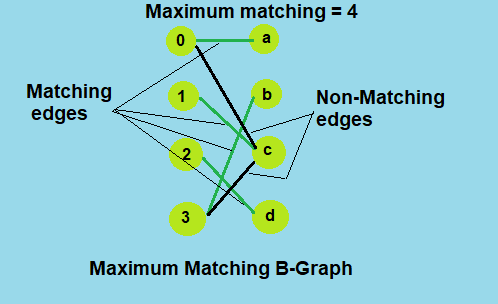
Matching and Not-Matching edges
Given a matching M, edges that are part of matching are called Matching edges and edges that are not part of M (or connect free nodes) are called Not-Matching edges.
Maximum cardinality matching
Given a bipartite graphs G = ( V = ( X , Y ) , E ) whose partition has the parts X and Y, with E denoting the edges of the graph, the goal is to find a matching with as many edges as possible. Equivalently, a matching that covers as many vertices as possible.

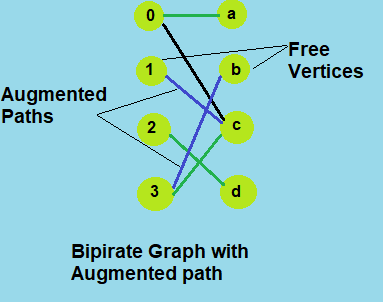
Augmenting paths
Given a matching M, an augmenting path is an alternating path that starts from and ends on free vertices. All single edge paths that start and end with free vertices are augmenting paths.

Algorithm

The Hopcroft Karp algorithm is based on below concept.

A matching M is not maximum if there exists an augmenting path. It is also true other way, i.e, a matching is maximum if no augmenting path exists.

So the idea is to one by one look for augmenting paths. And add the found paths to current matching.

The Hopcroft–Karp algorithm repeatedly increases the size of a partial matching by finding augmenting paths. Sequences of edges that alternate between being in and out of the matching, such that swapping which edges of the path are in and which are out of the matching produces a larger matching. However, instead of finding just a single augmenting path per iteration, the algorithm finds a maximal set of shortest augmenting paths. As a result, O(√V) iterations are needed. As BFS or DFS takes O(V + E) (i.e O(E) as E > V in genral) time per iteration, so overall time complexity of algorithm is O(E√V).

Steps

1) Initialize the Maximal Matching M as empty.
2) While there exists an Augmenting Path P
    Remove matching edges of P from M and add not-matching edges of P to M
    (This increases size of M by 1 as P starts and ends with a free vertex
    i.e. a node that is not part of matching.)
3) Return M. 

To understand the working of the algorithm, let's take an example of a bipartite graph of 8 vertices.

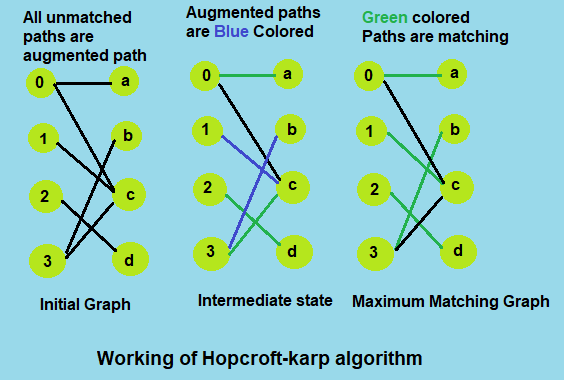
At initial state of the algorithm, all the possible paths are considered as augmented path. So we choose one and add it to the matching, now in intermediate state we check for augmented path with bfs algorithm, if any augmented path found then we start with free vertices to check for a matching with dfs algorithm. If a matching found then we update the result and repeat the same until any augmented path is available. At final state when no augmented path possible we reach the maximum matching which is 4 in the above example.

Implementation

Code in C++11

// C++ implementation of Hopcroft Karp algorithm for
// maximum matching
#include <iostream>
#include <cstdlib> 
#include <queue>
#include <list>
#include <climits>
#define NIL 0
#define INF INT_MAX

// A class to represent Bipartite graph for
// Hopcroft Karp implementation
class BGraph
{
    // m and n are number of vertices on left
    // and right sides of Bipartite Graph
    int m, n;

    // adj[u] stores adjacents of left side
    // vertex 'u'. The value of u ranges from 1 to m.
    // 0 is used for dummy vertex
    std::list<int> *adj;

    // pointers for hopcroftKarp()
    int *pair_u, *pair_v, *dist;

public:
    BGraph(int m, int n);     // Constructor
    void addEdge(int u, int v); // To add edge

    // Returns true if there is an augmenting path
    bool bfs();

    // Adds augmenting path if there is one beginning
    // with u
    bool dfs(int u);

    // Returns size of maximum matching
    int hopcroftKarpAlgorithm();
};

// Returns size of maximum matching
int BGraph::hopcroftKarpAlgorithm()
{
    // pair_u[u] stores pair of u in matching on left side of Bipartite Graph.
    // If u doesn't have any pair, then pair_u[u] is NIL
    pair_u = new int[m + 1];

    // pair_v[v] stores pair of v in matching on right side of Biparite Graph.
    // If v doesn't have any pair, then pair_u[v] is NIL
    pair_v = new int[n + 1];

    // dist[u] stores distance of left side vertices
    dist = new int[m + 1];

    // Initialize NIL as pair of all vertices
    for (int u = 0; u <= m; u++)
        pair_u[u] = NIL;
    for (int v = 0; v <= n; v++)
        pair_v[v] = NIL;

    // Initialize result
    int result = 0;

    // Keep updating the result while there is an
    // augmenting path possible.
    while (bfs())
    {
        // Find a free vertex to check for a matching
        for (int u = 1; u <= m; u++)

            // If current vertex is free and there is
            // an augmenting path from current vertex
            // then increment the result
            if (pair_u[u] == NIL && dfs(u))
                result++;
    }
    return result;
}

// Returns true if there is an augmenting path available, else returns false
bool BGraph::bfs()
{
    std::queue<int> q; //an integer queue for bfs

    // First layer of vertices (set distance as 0)
    for (int u = 1; u <= m; u++)
    {
        // If this is a free vertex, add it to queue
        if (pair_u[u] == NIL)
        {
            // u is not matched so distance is 0
            dist[u] = 0;
            q.push(u);
        }

        // Else set distance as infinite so that this vertex is considered next time for availibility
        else
            dist[u] = INF;
    }

    // Initialize distance to NIL as infinite
    dist[NIL] = INF;

    // q is going to contain vertices of left side only.
    while (!q.empty())
    {
        // dequeue a vertex
        int u = q.front();
        q.pop();

        // If this node is not NIL and can provide a shorter path to NIL then
        if (dist[u] < dist[NIL])
        {
            // Get all the adjacent vertices of the dequeued vertex u
            std::list<int>::iterator it;
            for (it = adj[u].begin(); it != adj[u].end(); ++it)
            {
                int v = *it;

                // If pair of v is not considered so far
                // i.e. (v, pair_v[v]) is not yet explored edge.
                if (dist[pair_v[v]] == INF)
                {
                    // Consider the pair and push it to queue
                    dist[pair_v[v]] = dist[u] + 1;
                    q.push(pair_v[v]);
                }
            }
        }
    }

    // If we could come back to NIL using alternating path of distinct
    // vertices then there is an augmenting path available
    return (dist[NIL] != INF);
}

// Returns true if there is an augmenting path beginning with free vertex u
bool BGraph::dfs(int u)
{
    if (u != NIL)
    {
        std::list<int>::iterator it;
        for (it = adj[u].begin(); it != adj[u].end(); ++it)
        {
            // Adjacent vertex of u
            int v = *it;

            // Follow the distances set by BFS search
            if (dist[pair_v[v]] == dist[u] + 1)
            {
                // If dfs for pair of v also returnn true then
                if (dfs(pair_v[v]) == true)
                {   // new matching possible, store the matching
                    pair_v[v] = u;
                    pair_u[u] = v;
                    return true;
                }
            }
        }

        // If there is no augmenting path beginning with u then.
        dist[u] = INF;
        return false;
    }
    return true;
}

// Constructor for initialization
BGraph::BGraph(int m, int n)
{
    this->m = m;
    this->n = n;
    adj = new std::list<int>[m + 1];
}

// function to add edge from u to v
void BGraph::addEdge(int u, int v)
{
    adj[u].push_back(v); // Add v to u’s list.
}

int main()
{
    int v1, v2, e;
    std::cin >> v1 >> v2 >> e; // vertices of left side, right side and edges
    BGraph g(v1, v2); // 
    int u, v;
    for (int i = 0; i < e; ++i)
    {
        std::cin >> u >> v;
        g.addEdge(u, v);
    }
  
    int res = g.hopcroftKarpAlgorithm();
    std::cout << "Maximum matching is " << res <<"\n";

    return 0;
}

Sample Input and Output

Input:
// vertices of left and right side and total edges
// B-Graph shown in the above example
4 4 6
1 1
1 3
2 3
3 4
4 3
4 2
Output:
// size of maximum matching
Maximum matching is 4

Complexity

Time complexity

• Hopcroft-karp algorithm takes O(E√V) time in worst case.

Space complexity

• Hopcroft-karp algorithm takes O(V) space in worst case.

References

• Wikipedia page on Hopcroft Karp algorithm
• Wikipedia page on matching(graph theory)