In this article, we will look at Image Compression using K-means Clustering which is an unsupervised learning algorithm. This is a lossy Image Compression technique.

Table of Contents:

1. Introduction
2. K-mean Clustering Algorithm
3. Image Compression Using Kmeans Clustering
4. Implementation of Image Compression using Kmeans Clustering

Pre-requisites:

• Image Compression: ML Techniques and Applications
• K means clustering
• Document Clustering using K Means
• Introduction to Clustering Algorithms

Introduction

In recent years, the development and demand for multimedia products has accelerated, resulting in network bandwidth and memory device storage shortages. As a result, image compression theory is becoming increasingly important for minimising data redundancy and saving more hardware space and transmission bandwidth.

Before getting to the implementation, let’s understand the K-mean Clustering Algorithm.

K-mean Clustering Algorithm

Clustering is the process of grouping data points that are comparable to one another into distinct groupings. For example, if we have a dataset that contains the locations of individuals from all over the world, we may divide it into distinct clusters based on states, with each cluster including just people from that state. K-Means clustering is a Machine Learning technique that divides data points into specified separate clusters, with each data point belonging to just one of these groups. If we look at the statistics behind it, we can see that K-Means Clustering, as the name implies, takes into consideration the arithmetic mean of the data point and forms clusters containing homogeneous data, that is, data points with comparable means in one cluster.

There are two steps in k-means clustering algorithm:

a) Assignment step – Each data point is assigned to the cluster whose center is nearest to it.

b) Update step – New means (centroids) are calculated from the data points assigned to the new clusters.

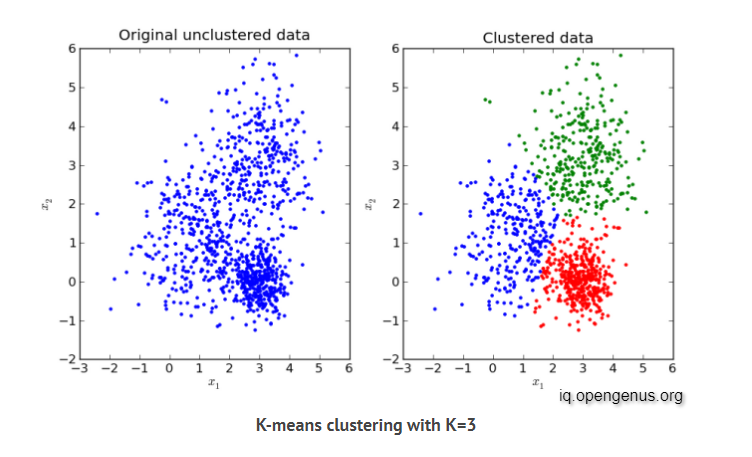
Image Compression Using Kmeans

The K-means algorithm can be used to compress the image. Unlike lossless compression, K-means uses lossy compression, so it is not possible to recover the original image from the compressed image. The larger the compression ratio, the larger the difference between the compressed image and the original image. The principle of K-means clustering algorithm for compressing images is as follow:

• Preferred number of selected clusters 𝐾 is very import, 𝐾 must be less than the number of image pixels 𝑁.

• Using each pixel of the image as a data point, clustering it with the K-means algorithm to obtain the centroid 𝝁௞.

• Storing the centroid and the index of the centroid of each pixel, so it not need to keep all the original data.

It is assumed that the original image has 𝑁 pixels, each pixel adopts the RGB three-color mode. each value of the RGB mode needs 8 bits, and 24𝑁 bits are required to directly store the original image. If K-means cluster compression is performed and the number of elements is 𝐾 with cluster center vector 𝝁௞, then the index of each pixel needs logଶ𝐾 bits to store. The K-means totally needs Nlog2𝐾 bits. In addition, you need to store k centroids, which need 24k bits, so you need a total of 24K + Nlog2𝐾 bits.

Now let's implement it.

Implementation of Image Compression using K-Means Clustering

Import the required libraries:

import numpy as np
from skimage import io
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

Then display the image you want to compress:

plt.rcParams['figure.figsize'] = (20, 12)
image = io.imread('images/penguin.jpg')
labels = plt.axes(xticks=[], yticks=[])
labels.imshow(image);

This is the original image which will be compressed:

Flatten the image:

rows = image.shape[0]
cols = image.shape[1]

image = image.reshape(rows*cols, 3)

Initialize kmean now:

kmeans = KMeans(n_clusters=64)
kmeans.fit(image)

Replace each pixel value with its nearby centroid:

compressed_image = kmeans.cluster_centers_[kmeans.labels_]
compressed_image = np.clip(compressed_image.astype('uint8'), 0, 255)

compressed_image = compressed_image.reshape(rows, cols, 3)

Save and display output image:

io.imsave('compressed_image_64.png', compressed_image)
io.imshow(compressed_image)
io.show()

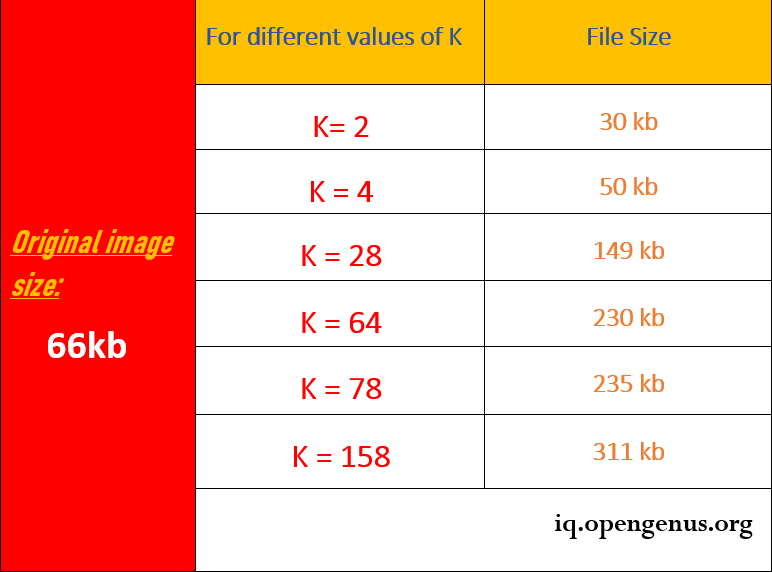
In this implementation we have tried different examples of k, below is the result of some different values of K:(have a look at the original image once to notice the difference(displayed above))

We now have seen the images with different variations of k, let's see what changes do this bring in the image size, basically lets compare the size of the original image vs the compressed image with different k variations:

Through this article at OpenGenus, you have an understanding of Image Compression using Kmeans Clustering Algorithm.