Karatsuba Algorithm (for fast integer multiplication)

Reading time: 20 minutes | Coding time: 5 minutes

The Karatsuba algorithm is a fast multiplication algorithm that uses a divide and conquer approach to multiply two numbers. It was discovered by Anatoly Karatsuba in 1960 and published in 1962.
This happens to be the first algorithm to demonstrate that multiplication can be performed at a lower complexity than O(N^2) which is by following the classical multiplication technique. Using this algorithm, multiplication of two n-digit numbers is reduced from O(N^2) to O(N^(log 3) that is O(N^1.585).

In this article at OpenGenus, we will explore this game changing algorithm to perform fast integer multiplication.

$$n^(log_2 3) \approx n^(1.585)$$

It is faster than the naive algorithm for multiplying two numbers which requires $n^2$ single-digit products. As an example, the Karatsuba algorithm requires 3^10 = 59,049 single-digit multiplications to multiply two 1024-digit numbers (n = 1024 = 2^10), whereas the classical algorithm requires (2^10)^2 = 1,048,576 single-digit multiplications.

The key idea is to reduce the four sub-problems in multiplication to three unique problems. Thus, on calculating the three unique sub-problems, the original four sub-problems are solved using addition or subtraction operation. Hence, the speed-up.

Explanation

Basically Karatsuba stated that if we have to multiply two n-digit numbers x and y, this can be done with the following operations, assuming that B is the base of m and m < n (for instance: m = n/2)

First both numbers x and y can be represented as x1,x2 and y1,y2 with the following formula.

$$x = x1 * B^m + x2$$
$$y = y1 * B^m + y2$$

The product x X y becomes the following product:

$$xy = (x1 * B^m + x2)(y1 * B^m + y2)$$
$$ => xy = x1 * y1 * B^(2m) + x1 * y2 * B^m + x2 * y1 * B^m + x2 * y2$$

Observe that there are 4 sub-problems: X1 * Y1, X1 * Y2, X2 * Y1 and X2 * Y2

With a clever insight, we can reduce this to 3 sub-problems and hence, the acceleration.

Let $a = x1 * y1$, $b = x1 * y2 + x2 * y1$ and $c = x2 * y2$

Finally, x X y becomes:

$$xy = a * B^(2m) + b * B^m + c$$

That is why Karatsuba came up with the brilliant idea to calculate b with the following formula:

$$b = (x1 + x2)(y1 + y2) - a - c$$

Example

Consider the following multiplication: 47 x 78
 
x = 47
x = 4 * 10 + 7
 
x1 = 4
x2 = 7
 
y = 78
y = 7 * 10 + 8
 
y1 = 7
y2 = 8
 
a = x1 * y1 = 4 * 7 = 28
c = x2 * y2 = 7 * 8 = 56
b = (x1 + x2)(y1 + y2) - a - c = 11 * 15 - 28 - 56

11 * 15 can in turn be multiplied using Karatsuba Algorithm

Complexity

Assuming that we replace two of the multiplications with only one makes the program faster. The question is how fast. Karatsuba improves the multiplication process by replacing the initial complexity of $O(n^2)$ by $O(n^(log3))$, which as you can see on the diagram below is much faster for big n.

$$T(n)=3 * T(n/2) + O(n)$$

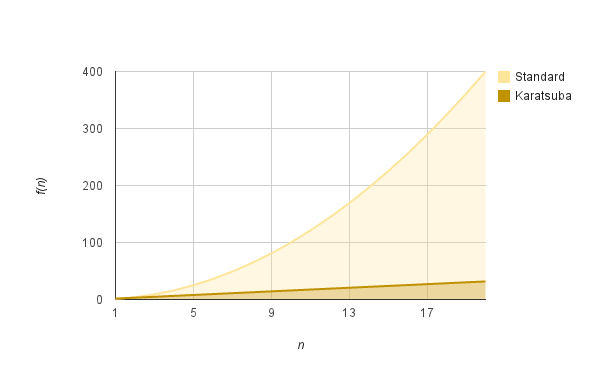
O(n^2) grows much faster than O(n^lg3)

Pseudocode

procedure karatsuba(num1, num2)
  if (num1 < 10) or (num2 < 10)
    return num1*num2
    
  *calculates the size of the numbers*
  m = max(size_base10(num1), size_base10(num2))
  m2 = m/2
  
  *split the digit sequences about the middle*
  high1, low1 = split_at(num1, m2)
  high2, low2 = split_at(num2, m2)
  
  *3 calls made to numbers approximately half the size*
  z0 = karatsuba(low1, low2)
  z1 = karatsuba((low1 + high1), (low2 + high2))
  z2 = karatsuba(high1, high2)
  return (z2 * 10 ^ (2 * m2)) + ((z1 - z2 - z0) * 10 ^ (m2)) + (z0)

Implementations

• Python

        def karatsuba(x,y):
            if len(str(x)) == 1 or len(str(y)) == 1:
                return x*y
            else:
                n = max(len(str(x)),len(str(y)))
                nby2 = n / 2
                a = x / 10**(nby2)
                b = x % 10**(nby2)
                c = y / 10**(nby2)
                d = y % 10**(nby2)
                ac = karatsuba(a,c)
                bd = karatsuba(b,d)
                ad_plus_bc = karatsuba(a+b,c+d) - ac - bd
                prod = ac * 10**(2*nby2) + (ad_plus_bc * 10**nby2) + bd
                return prod

Application

The Karatsuba algorithm is very efficient in tasks that invlove integer multiplication. It can also be useful for polynomial multiplications.

It is to be noted that faster multiplication algorithms do exist.