Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Problem Statement

Given a list of words ‘WORDLIST’, find the longest perfect word. A perfect word is a word in which all the possible prefixes are present in ‘WORDLIST’.

If more than one perfect word of the same length is present in the ‘WORDLIST’, return the word with the smallest lexicographical order. You can return an empty string if no such word is possible for the given input.

Input

["w", "wo", "wor", "wow", "worm", "work"]
["w","wo","wor","worl","world"]
["a","banana","app","appl","ap","apply","apple"]

Output

"work"
"world"
"apple"

Explanation

In the first input "worm" and "work" both are the longest perfect words as all the prefixes of these two words are present in the list. But "work" is lexicographically smaller than "worm". So, the correct output is "work".

In the second input, each word is a perfect word but "world" is the longest. So, the correct output is "world".

In the third input the strings, "a", "ap", "app", "appl", "apply" and "apple" are perfect strings. "apply" and "apple" is the longest perfect strings but "apple" is lexicographically smaller than "apply". So, the correct output is "apple".

Solution

The problem can be solved efficiently using HashSet as well as Trie data structure. We will see both approaches. We will be writing the code for the same in C++ as well as Java languages.

Approach 1: The brute force approach

The brute force approach to solve this problem would be to iterate through the wordlist, for each word iterate through its characters and get prefixes and check if these prefixes are present in the wordlist by iterating through the wordlist again.

Algorithm

Create a variable 'LONGEST' to keep track of the longest word and initialize it as an empty string
Iterate through the "WORDLIST":
- Create a variable "PREFIX" which holds the prefixes of the "CURRENT_WORD"
- For "CURRENT_WORD" iterate through the characters:
  - Add the "CURRENT_CHARACTER to the "PREFIX" variable.
  - Check if the "PREFIX" is present in the "WORDLIST"
  - To check if the "PREFIX" is present in the "WORDLIST":
    - Create a flag "PRESENT" and initialize it with a false value
    - Iterate through the "WORDLIST":
      - If the "PREFIX" is present, set the value of "PRESENT" to be true and break the loop
    - return the value of "PRESENT"
- If all the prefixes of "CURRENT_WORD" are present in the "WORDLIST":
  - If the size of "CRRENT_WORD" is greater than the size of "LONGEST", set the "LONGEST" to be "CRRENT_WORD"
  - If the size of "CURRENT_WORD" is equal to the size of "LONGEST", set the value of "LONGEST" to be lexicographically smaller between "CURRENT_WORD" and "LONGEST"
Return the value of "LONGEST"

Here is the C++ implementation of the above algorithm

#include <iostream>
#include <vector>
using namespace std;

bool isPresent(vector<string>& words, string str) {
	bool present = false;
	for(string word: words) {
		if(word == str) {
			present = true;
			break;
		}
	}

	return present;
}

string longestPerfctWord(vector<string> &words) {
	string longest = "";

	for(auto word: words) {
		string prefix = "";
		bool allPrefixesPresent = true;

		for(auto ch: word) {
			prefix.push_back(ch);
			if(!isPresent(words, prefix)) {
				allPrefixesPresent = false;
				break;
			}
		}	

		if(allPrefixesPresent) {
			if(word.size() > longest.size())
				longest = word;

			if(word.size() == longest.size())
				longest = (word < longest)? word: longest;
		}
	}


	return longest;
}

int main()
{
	vector<string> v1 = {"w", "wo", "wor", "wow", "worm", "work"};
	vector<string> v2 = {"w","wo","wor","worl","world"};
	vector<string> v3 = {"a","banana","app","appl","ap","apply","apple"};

	cout << longestPerfctWord(v1) << endl; //output: work
	cout << longestPerfctWord(v2) << endl; //output: world
	cout << longestPerfctWord(v3) << endl; //output: apple
}

Here is the Java implementation of the above algorithm

import java.util.*;

class Solution {
	public static boolean isPresent(String[] words, String str) {
		for(String word: words) {
			if(word.equals(str))
				return true;
		}

		return false;
	}

	public static String longestPerfectWord(String[] words) {
		String longest = "";

		for(String word: words) {
			String prefix = "";
			boolean allPrefixesPresent = true;

			for(int i = 0;i < word.length();++i) {
				prefix += Character.toString(word.charAt(i));
				if(!isPresent(words, prefix)) {
					allPrefixesPresent = false;
					break;
				}
			}

			if(allPrefixesPresent) {
				if(word.length() > longest.length())
					longest = word;

				if(word.length() == longest.length())
					longest = (word.compareTo(longest) < 0) ? word: longest;
			}
		}

		return longest;
	}
	public static void main(String[] args) {
		String[] v1 = {"w", "wo", "wor", "wow", "worm", "work"};
		String[] v2 = {"w","wo","wor","worl","world"};
		String[] v3 = {"a","banana","app","appl","ap","apply","apple"};

		System.out.println(longestPerfectWord(v1)); //output: work
		System.out.println(longestPerfectWord(v2)); //output: world
		System.out.println(longestPerfectWord(v3)); //output: apple
	}
}

Time Complexity: We can see all the prefixes are created for a word. So, if the lenght of the word is w then w prefixes will be created. Since there are n words in the wordlist, Σ(w) prefixes will be created. Now, all the prefixes are searched into the wordlist and this takes O(n) time. This whole procedure happends for all the elements present in the worldlist.

So, the time complexity = O(n * Σ(w) * n) = O(n² * Σ(w)) which can be approximated to O(n³).

Space Complexity:Since not extra space is used for the operation, so the space complexity would be O(1).

Approach 2: Using HashSet

The idea behind using HashSet is that it provides O(1) lookup time. So, the operation of checking if the particular prefix is present in the wordlist or not, won't take O(n) time and can be completed in O(1) time.

Algorithm

Create a ‘HASH_SET’ to store the 'WORDLIST' for faster lookup.
Create a "LONGEST" to store the longest perfect string and initialize it as an empty string
For ‘CURRENT_STRING’ from the beginning to the end of the ‘WORDLIST’, do:
- Insert ‘CURRENT_STRING’ into ‘HASH_SET’.
For ‘CURRENT_STRING’ from the beginning to the end of the ‘WORDLIST’, do:
- Check if the "CURRENT_STRING" is perfect
- To check if the "CURRENT_STRING" is perfect
  - Check if all the prefixes of the "CURRENT_STRING" are present in the "HAHS_SET"
- If the "CURRENT_STRING" is perfect and the length of the string is greater than the length of "LONGEST" set the "LONGEST" to be "CURRENT_STRING"
- If the "CURRENT_STRING" is perfect and the length of the string is equal to the length of "LONGEST" set the "LONGEST" to be one that is lexicographically smaller.
Return "LONGEST"

C++ Implementation

#include<iostream>
#include <vector>
#include <unordered_set>
#include <string>
using namespace std;

unordered_set<string> s;

bool isPerfect(string word) {
	string prefix = "";
	for(char ch: word) {
		prefix.push_back(ch);
		if(s.find(prefix) == s.end())
			return false;
	}

	return true;
}


string longestPerfectString(vector<string>& words) {
	for(auto word: words) {
		s.insert(word);
	}

	string longest = "";
	for(auto word: words) {
		if(word.size() >= longest.size() && isPerfect(word))
			if(word.size() > longest.size() || (word < longest))
				longest = word;
	}

	return longest;
}

int main() {
	vector<string> v1 = {"w", "wo", "wor", "wow", "worm", "work"};
	vector<string> v2 = {"w","wo","wor","worl","world"};
	vector<string> v3 = {"a","banana","app","appl","ap","apply","apple"};

	cout << longestPerfectString(v1) << endl; //output: work
	cout << longestPerfectString(v2) << endl; //output: world
	cout << longestPerfectString(v3) << endl; //output: apple
}

Java Implementation

import java.util.*;

class Solution {
    static HashSet<String> set = new HashSet<>();
    
    public static boolean isPerfect(String word) {
        int n = word.length();
        String s = "";
        for(int i = 0;i < n;++i) {
            s += Character.toString(word.charAt(i));
            if(!set.contains(s))
                return false;
        }
        
        return true;
    }
    
    
    public static String longestPerfectWord(String[] words) {
        
        for(String word: words) {
            set.add(word);
        }
        
        String longest = "";
        for(String word: words) {
            if(word.length() >= longest.length() && isPerfect(word)) {
                if(word.length() > longest.length() || (word.compareTo(longest) < 0))
                    longest = word;
            }
        }
        
        return longest;
    }
    
    public static void main(String[] args) {
		String[] v1 = {"w", "wo", "wor", "wow", "worm", "work"};
		String[] v2 = {"w","wo","wor","worl","world"};
		String[] v3 = {"a","banana","app","appl","ap","apply","apple"};

		System.out.println(longestPerfectWord(v1)); //output: work
		System.out.println(longestPerfectWord(v2)); //output: world
		System.out.println(longestPerfectWord(v3)); //output: apple
	}
}

Time Complexity: Checking each prefix requires a linear-time operation. For a word with the length ‘W’, the maximum length of a prefix is ‘W’. The time complexity to check the maximum length prefix in the set is O(W). For the word ‘W’ in the ‘WORDLIST’, all the possible prefixes are checked. So, the time complexity to check all prefixes of a word is O(W^2). To check prefixes of all the words, the time complexity is O(∑W_i²), where Wi represents each word from the ‘WORDLIST’.

Space Complexity: To create all prefixes of a word, extra space is required. So, the space complexity is O(∑W_i²), where Wi represents each word from the ‘WORDLIST’.

Approach 3: Using Trie

A trie data structure is a tree-like data structure that is, most of the time, used to insert and search words in a dictionary. The below picture gives an idea of what a trie data structure looks like.
trie

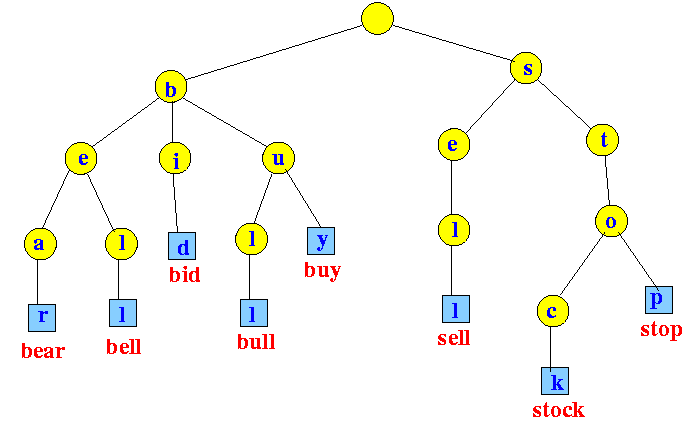
As can be seen in the picture, the trie data structure consists of nodes and unlike the nodes of a binary tree, it can reference many other nodes.

If we observe it, we see that if a trie data structure contains a word, all its prefixes are also contained.

For example, in the above picture the right most word inserted in the trie is "stop" and all its prefixes- "s", "st", "sto", are also present in the trie.
These prefixes can be searched in linear time. So, it is a great fit for our problem.

Algorithm

Create a "TRIE" to store the words in the "WORDLIST"
Create a variable "LONGEST" that tracks the longest perfect string
For "WORD" from the beginning to the end in "WORDLIST":
- If the length of the "WORD" is greater than the length of the length of the "LONGEST" and "WORD" is a perfect string(to check if the string is perfect we will check if all the prefixes are present in the trie):
  - If the length of the "WORD" is greater than the length of the "LONGEST":
    - Set the "LONGEST" to be "WORD"
  - If the length of the "WORD" is equal to the length of the "LONGEST" and "WORD" is lexicographically smaller than "LONGEST":
    - Set the "LONGEST" to be "WORD"
Return the value of "LONGEST"

C++ Implementation

#include <iostream>
#include <vector>
using namespace std;

struct Node {
	Node* links[26];
	bool end = false;

	bool containsKey(char ch) {
		return links[ch - 'a'] != nullptr;
	}

	void put(char ch, Node* node) {
		links[ch - 'a'] = node;
	}

	Node* get(char ch) {
		return links[ch - 'a'];
	}

	void setEnd() {
		end = true;
	}

	bool isEnd() {
		return end;
	}
};

class Trie {
private:
	Node* root;

public:
	Trie() {
		root = new Node();
	}

	void insert(string word) {
		Node* node = root;

		for(auto ch: word) {
			if(!node->containsKey(ch))
				node->put(ch, new Node());

			node = node->get(ch);
		}

		node->setEnd();
	}

	void insertAll(vector<string>& words) {
		for(auto word: words)
			insert(word);
	}

	bool isPerfect(string word) {
		Node* node = root;
		for(auto ch: word) {
			if(!node->containsKey(ch))
				return false;
			
			node = node->get(ch);
			if(!node->isEnd())
				return false;
		}

		return true;
	}
};

//We are going to implement this method to return the longest perfect string
string longestPerfectString(vector<string>& words) {
	Trie* trie = new Trie();
	trie->insertAll(words);

	string longest = "";
	for(auto word: words) {
		if(word.size() >= longest.size() && trie->isPerfect(word)) {
			if(word.size() > longest.size() || (word < longest))
				longest = word;
		}
	}

	return longest;
}

int main()
{
	vector<string> v1 = {"w", "wo", "wor", "wow", "worm", "work"};
	vector<string> v2 = {"w","wo","wor","worl","world"};
	vector<string> v3 = {"a","banana","app","appl","ap","apply","apple"};

	cout << longestPerfectString(v1) << endl; //output: work
	cout << longestPerfectString(v2) << endl; //output: world
	cout << longestPerfectString(v3) << endl; //output: apple
	return 0;
}

Java Implementation

class Node {
    private Node links[];
    private boolean flag;
    
    public Node() {
        this.links = new Node[26];
        this.flag = false;
    }
    
    public boolean containsKey(char ch) {
        return this.links[ch - 'a'] != null;
    }
    
    public Node get(char ch) {
        return this.links[ch - 'a'];
    }
    
    public void put(char ch, Node node) {
        this.links[ch - 'a'] = node;
    }
    
    public void setEnd() {
        this.flag = true;
    }
    
    public boolean isEnd() {
        return this.flag;
    }
}

class Trie {
    private Node root;
    
    public Trie() {
        root = new Node();
    }
    
    private void insert(String word) {
        Node node = root;
        for(int i = 0;i < word.length();++i) {
            if(!node.containsKey(word.charAt(i))) {
                node.put(word.charAt(i), new Node());
            }
            
            node = node.get(word.charAt(i));
        }
        node.setEnd();
    }
    
    public void insertAll(String[] words) {
        for(String word: words)
            insert(word);
    }
    
    public boolean isPerfect(String word) {
        Node node = root;
        int n = word.length();
        for(int i = 0;i < n;++i) {
            if(node.containsKey(word.charAt(i)))  {
                node = node.get(word.charAt(i));
                if(!node.isEnd())
                    return false;
            } else {
                return false;
            }
        }
        
        return true;
    }
    
    public String getLongestPerfect(String[] arr) {
        String longest = "";

        for(String word: arr) {
            if(word.length() >= longest.length() && isPerfect(word)) {
                if(word.length() > longest.length())
                    longest = word;

                if(word.length() == longest.length()) {
                    if(word.compareTo(longest) < 0)
                        longest = word;
                }
            }
        }
        
        return longest;
    }
}

class Solution {
   
    public static String longestPerfectWord(String[] words) {
        Trie trie = new Trie();
        trie.insertAll(words);
        return trie.getLongestPerfect(words);
    }

    public static void main(String[] args) {
        String[] v1 = {"w", "wo", "wor", "wow", "worm", "work"};
		String[] v2 = {"w","wo","wor","worl","world"};
		String[] v3 = {"a","banana","app","appl","ap","apply","apple"};

		System.out.println(longestPerfectWord(v1)); //output: work
		System.out.println(longestPerfectWord(v2)); //output: world
		System.out.println(longestPerfectWord(v3)); //output: apple
    }
}

Time Complexity: : In the worst case, we may need to traverse through the whole trie data structure. The trie data structure contains all the letters of al the words. So, the time complexity of this method is O(⅀W_i), where Wi represents the length of the ith word in ‘WORDLIST’.

Space Complexity: An additional space is required to store all the words in the trie data structure. So, the space complexity is O(⅀W_i), where Wi represents the length of the ith word in ‘WORDLIST’.

Happy Coding!🤗🤗🤗
See you!👋👋👋

Longest word in dictionary with all prefixes

trie String Algorithms Algorithms

Problem Statement

Input

Output

Explanation

Solution

Approach 1: The brute force approach

Algorithm

Here is the C++ implementation of the above algorithm

Here is the Java implementation of the above algorithm

Approach 2: Using HashSet

Algorithm

C++ Implementation

Java Implementation

Approach 3: Using Trie

Algorithm

C++ Implementation

Java Implementation

Data Structure used for Recursion

Is DevOps a role or culture?