
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 5 minutes
Sorting is a process of arranging elements in a group in a particular order, i.e., ascending order, descending order, alphabetic order, etc.
Sorting a list of elements is a very common operation. A sequential sorting algorithm may not be efficient enough when we have to sort a huge volume of data. Therefore, parallel algorithms are used in sorting.
Parallel Algorithm : A parallel algorithm is an algorithm that can execute several instructions simultaneously on different processing devices and then combine all the individual outputs to produce the final result.
Odd Even Sort uses parallel algorithm which is based on bubble sort technique.
It is also known as Brick Sort.
Algorithm
- It compares two adjacent numbers and switches them, if the first number is greater than the second number to get an ascending order list.
- The opposite case applies for a descending order series.
- Odd-Even transposition sort operates in two phases − odd phase and even phase.
- In both the phases, processes exchange numbers with their adjacent number in the right.
Pseudo Code
procedure ODD-EVEN_PAR (n)
begin
id := process's label
for i := 1 to n do
begin
if i is odd and id is odd then
compare-exchange_min(id + 1);
else
compare-exchange_max(id - 1);
if i is even and id is even then
compare-exchange_min(id + 1);
else
compare-exchange_max(id - 1);
end for
end ODD-EVEN_PAR
Example
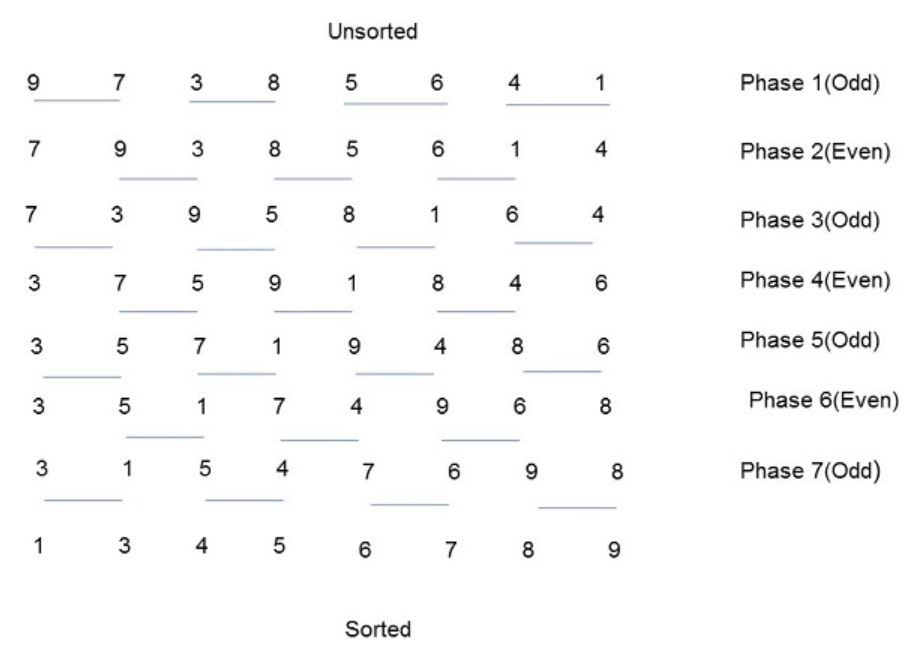
Unsorted : 9 7 3 8 5 6 4 1
Phase 1 : 9 > 7 => Swap , 4 > 1 => Swap
Phase 2 : 9 > 3 => Swap , 8 > 5 => Swap , 6 > 1 => Swap
Phase 3 : 7 > 3 => Swap , 9 > 5 => Swap , 8 > 1 => Swap , 6 > 4 => Swap
Phase 4 : 7 > 5 => Swap , 9 > 1 => Swap , 8 > 4 => Swap
Phase 5 : 7 > 1 => Swap , 9 > 4 => Swap , 8 > 6 => Swap
Phase 6 : 5 > 1 => Swap , 7 > 4 => Swap , 9 > 6 => Swap
Phase 7 : 3 > 1 => Swap , 5 > 4 => Swap , 7 > 6 => Swap , 9 > 8 => Swap
Sorted : 1 3 4 5 6 7 8 9
Implementation
- C++
- Python
C++
// A C++ Program to implement Odd-Even / Brick Sort
#include<bits/stdc++.h>
using namespace std;
// A function to sort the algorithm using Odd Even sort
void oddEvenSort(int arr[], int n)
{
bool isSorted = false; // Initially array is unsorted
while (!isSorted)
{
isSorted = true;
// Perform Bubble sort on odd indexed element
for (int i=1; i<=n-2; i=i+2)
{
if (arr[i] > arr[i+1])
{
swap(arr[i], arr[i+1]);
isSorted = false;
}
}
// Perform Bubble sort on even indexed element
for (int i=0; i<=n-2; i=i+2)
{
if (arr[i] > arr[i+1])
{
swap(arr[i], arr[i+1]);
isSorted = false;
}
}
}
return;
}
// A utility function ot print an array of size n
void printArray(int arr[], int n)
{
for (int i=0; i < n; i++)
cout << arr[i] << " ";
cout << "\n";
}
// Driver program to test above functions.
int main()
{
int arr[] = {9,7,3,8,5,6,4,1};
int n = sizeof(arr)/sizeof(arr[0]);
oddEvenSort(arr, n);
printArray(arr, n);
return (0);
}
Python
# Python Program to implement
# Odd-Even / Brick Sort
def oddEvenSort(arr, n):
# Initially array is unsorted
isSorted = 0
while isSorted == 0:
isSorted = 1
temp = 0
for i in range(1, n-1, 2):
if arr[i] > arr[i+1]:
arr[i], arr[i+1] = arr[i+1], arr[i]
isSorted = 0
for i in range(0, n-1, 2):
if arr[i] > arr[i+1]:
arr[i], arr[i+1] = arr[i+1], arr[i]
isSorted = 0
return
arr = [9,7,3,8,5,6,4,1]
n = len(arr)
oddEvenSort(arr, n);
for i in range(0, n):
print(arr[i], end = ' ')
Complexity
- Worst case time complexity:
Θ(n*n) - Average case time complexity:
Θ(n*n) - Best case time complexity:
Θ(n) - Space complexity:
Θ(1)
