We will look at the very promising but not very common activation function called SELU (Scaled Exponential Linear Unit) and understand its main advantages over other activation functions like ReLU (Rectified Linear Unit). This article presents lots of essential points about this function.

Table Of Contents:

1. Brief recap of the pre-requisites

   • What are Neural Networks?
   • What is an Activation Function?
   • What is ReLU?

2. What is SELU?

3. Implementing SELU function in Python

4. What is normalization?

5. Why are ReLUs not enough?

6. Advantages of SELU

7. Disadvantages of SELU

Pre-requisites:

• Activation Functions in Machine Learning
• Types of Activation Function
• Linear Activation Function
• ReLU (Rectified Linear Unit) Activation Function

Brief recap of the pre-requisites:

What is Neural Networks?

Artificial neural networks are computer systems based on the human brain's neural networks. They consist of Node layers; they have an input layer, one or more hidden levels, and an output layer. Each node, or artificial neuron, is linked to another and has its own weight and threshold. When a node's output reaches a specific level, it is activated and begins transferring data to the network's next layer. Otherwise, no data is transferred to the network's next layer.

What is an Activation Function?

The activation function is a simple mathematical function that converts a given input into a desired output within a specific range.

The activation function calculates a weighted total and then adds bias to it to determine whether a neuron should be activated or not. The activation function aims to introduce non-linearity into a neuron's output.
Our model will behave like a linear regression model with low learning potential if we don't include an activation function.

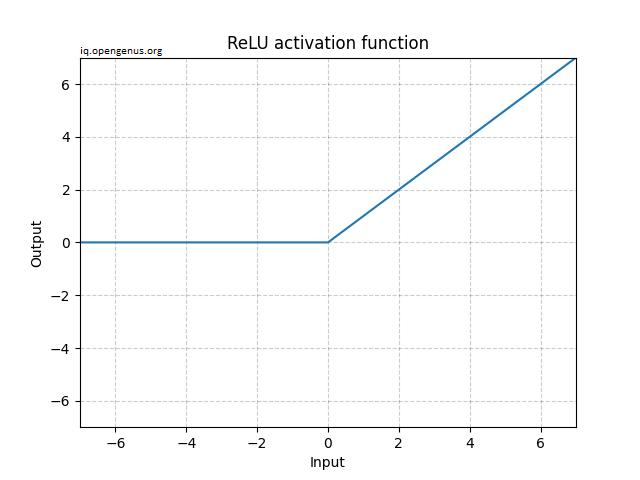
What is ReLU?

The rectified linear activation function (ReLU) is a piecewise non-linear function that outputs the input directly if it is positive and zero otherwise.

Mathematically, it is expressed as:
$$f(x) = \max(0, x)$$

Graphically, it is represented as:

What is SELU?

SELUs, or Scaled Exponential Linear Units, are activation functions that induce self-normalization. SELU network neuronal activations automatically converge to a zero mean and unit variance.

Mathematically, it is expressed as:

$$f(x) = \lambda x \ \ \ \ \ \ \ \text{if} \ \ x > 0 $$ $$f(x)= \lambda \alpha (e^x - 1) \ \ \ \ \ \ \ \text{if} \ \ x \leq 0$$
Where $\lambda$ and $\alpha$ are the following approximate values:
$$ \lambda \approx 1.0507009873554804934193349852946 $$ $$ a \approx 1.6732632423543772848170429916717 $$

If $x$ is larger than 0, the output result is $x$ multiplied by lambda $lambda$. If the input value $x$ is less than or equal to zero, we have a function that goes up to $0$, which is our output $y$, when $x$ is zero. Essentially, when $x$ is smaller than zero, we take the exponential of the x-value minus 1, then we multiply it with alpha $\alpha$ and lambda $\lambda$.

Graphically, it is represented as:

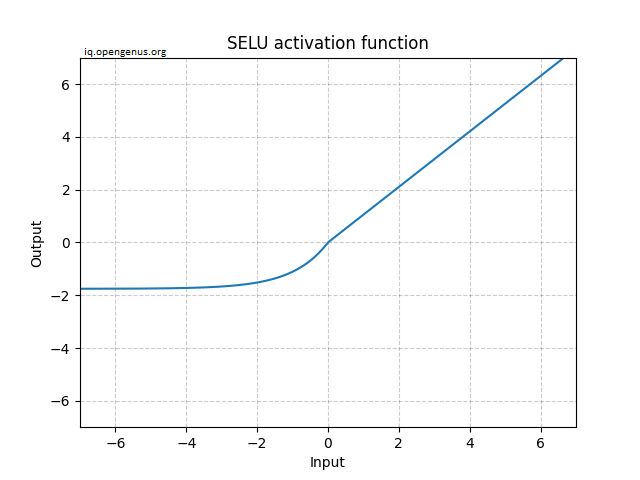Unlike ReLU, it can get below 0, allowing the system to have a zero average output. As a result, the model may converge faster.

Implementing SELU function in Python

 

Defining the SELU function to resemble the mathematical equation:

def SELU(x, lambdaa = 1.0507, alpha = 1.6732):
    if x >= 0:
        return lambdaa * x
    else:
        return lambdaa * alpha * (np.exp(x) - 1)

 

Now, we'll test out the function by giving some input values and plotting the result using pyplot from the matplotlib library. The input range of values is -5 to 10. We apply our defined function to this set of input values.

from matplotlib import pyplot
import numpy as np

series_in = [x for x in range(-5, 10)]
# apply SELU on each input
series_out = [SELU(x) for x in input]
# plot our result
pyplot.plot(series_in, series_out)
pyplot.show()

 

The output graph will be:

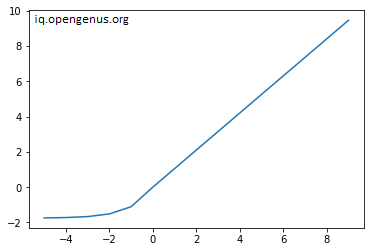
We can see from the plot that all the negative values have been set to be exponential, and the positive values are linearly presented.

What is normalization?

SELU is known to be a self-normalizing function, but what is normalization?

Normalization is a data preparation technique that involves changing the values of numeric columns in a dataset to a common scale. This is usually used when the attributes of the dataset have different ranges.

There is 3 types of normalization:

1. Input normalization: One example is scaling the pixel values of grey-scale photographs (0–255) to values between zero and one
2. Batch normalization: Values are changed between each layer of the network so that their mean is zero and their standard deviation is one.
3. Internal normalization: this is where SELU's magic happens. The key idea is that each layer keeps the previous layer's mean and variance.

So, how does SELU make this possible? More precisely, How can it adjust the mean and variance? Let's take another look at the graph:

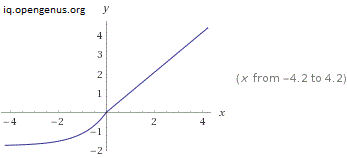
For y to change the mean, the activation function needs both positive and negative values. Both options are available here. It is also why ReLU ReLU isn't a good option for a self-normalizing activation function since it can not output negative values.

Why are ReLUs insufficient?

Artificial neural networks learn by a gradient-based process called backpropagation. The basic idea is that a network's weights and biases are updated in the direction of the gradients.

Backpropagation can cause gradients to become too small, leading to a problem named  vanishing gradients. If our network has vanishing gradients, the weights won't adjust, and learning will stop. Deep networks, at a high level, backpropagate a large number of gradients where when gradients approach 0, the entire product drops.

One problem with ReLUs is that they can become trapped in a dead state. That is, the weights vary so much and the next iteration's z is very small that the activation function is locked on the left side of zero. The affected cell can no longer contribute to the network's learning, and its gradient remains zero. If this occurs to a large number of cells in your network, the trained network's power remains below its theoretical possibilities, resulting in dying ReLUs.

Advantages of SELU

1. Like ReLU, SELU does not have vanishing gradient problem and hence, is used in deep neural networks.
2. Compared to ReLUs, SELUs cannot die.
3. SELUs learn faster and better than other activation functions without needing further procession. Moreover, other activation function combined with batch normalization cannot compete with SELUs.

Disadvantages of SELU

1. SELU is a relatively new activation function so it is not yet used widely in practice. ReLU stays as the preferred option.
2. More research on architectures such as CNNs and RNNs using SELUs is needed for wide-spread industry use.