Binary search is a simple yet efficient searching algorithm which is used to search a particular element's position in a given sorted array/vector.
In this algorithm the targeted element is compared with middle element. If both elements are equal then position of middle element is returned and hence targeted element is found.

If both elements are unequal then if targeted element is less or more than middle element we discard the lower or upper half and the search continues by finding new middle element.

We have covered 3 approaches:

• Recursive implementation
• Iterative implementation
• Using STL functions

Algorithm

1. Start with the middle element:
   • If the target value is equal to the middle element of the array, then return the index of the middle element.
   • If not, then compare the middle element with the target value,
     • If the target value is greater than the number in the middle index, then pick the elements to the right of the middle index, and start with Step 1.
     • If the target value is less than the number in the middle index, then pick the elements to the left of the middle index, and start with Step 1.
2. When a match is found, return the index of the element matched.
3. If no match is found, then return -1

Implementation Methods

It can be implemented in following three ways:

1. Iterative Function
2. Recursive Function
3. In-built Function

1) Iterative Method

Piece-wise code explanation

#include <bits/stdc++.h>
using namespace std;

Here we have included the header files. This template is common for all C++ codes.

int main()
{
    int a[] = { 10, 12, 20, 32, 50, 55, 65, 80, 99 };
    int element = 12;
    int size = sizeof(a) / sizeof(a[0]); 
    sort(a, a + size);
    int result = BinarySearch(a, 0, size - 1, element); 
    if(result == -1)
        cout<<"Element is not present in array";
    else
        cout<<"Element is present at index "<< result;
    return 0;
}

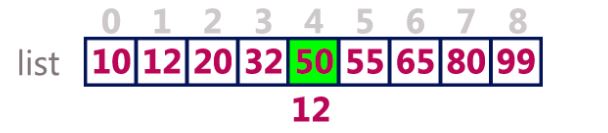
This is the main function. We have taken an array of size 9. Its elements are 10, 12, 20, 32, 50, 55, 65, 80 and 99. Remeber the indexing of an array starts from 0. For example -> 10 is present at index 0 and 99 is present at index 8.
Then we have taken the element which we need to search in that array. Here that element is 12.

We will sort the array first as Binary Search works on sorted arrays only. But in our case it is already sorted.
Now we have called a function "BinarySearch" which will give the index of the element in the array if it is present otherwise -1 which indicates that the element is not present in the given array.

int BinarySearch(int sorted_array[], int left, int right, int element) 
{ 
     while (left <= right) 
    { 

The function "BinarySearch" takes an sorted array, leftmost index (= 0), rightmost index (= 8) and the element to be searched.

First we will check whether the left index is less than the right index or not. If left > right, then it means that we have crossed the middle point of the array we are considering and the element has not been found yet which clearly means that the element is not present in the array. We will simply return -1.

int middle = (left + right) / 2; 
if (sorted_array[middle] == element) 
            return middle; 

Now we will calculate the middle index by using the above formula. In our case it comes out to be (0+8)/2 = 4.

Now we will check if the element to be searched is equal to the element present at the middle index (element=50) or not.
Clearly, 50 is not equal to 12 so we split the array into two sub arrays i.e. left sub-array and right sub-array.

if (sorted_array[middle] < element) 
            left = middle + 1;
else
            right = middle - 1; 

After knowing that the element is not equal to the middle element, we will check that whether it is present in the left of it or right of it i.e in left sub-array or right sub-array.

Here we are reducing the complexity by just searching te half part of the array.
If the element is less than the element then it means that it is present to the left of it or else to the right of it.

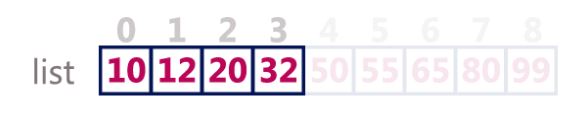
Since 12 < 50. We will consider now only left sub-array to search it.

Now again while loop will run but with different left and right indices. Left = 0 (leftmost index of left sub-array) and Right = 3 (rightmost index of the left sub-array)
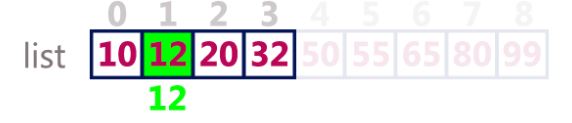
Now middle index = (0+3)/2 = 1.
And element present at index 1 = 12 which is the element we want to search. Hence we will return the index of this element which is 1 to the main function.

Full Code

#include <bits/stdc++.h>
using namespace std;
int BinarySearch(int sorted_array[], int left, int right, int element) 
{ 
     while (left <= right) 
    { 
        int middle = (left + right) / 2; 
        // Check if element is present at middle position or not 
        if (sorted_array[middle] == element) 
            return middle; 
        // If element is greater, ignore left half 
        if (sorted_array[middle] < element) 
            left = middle + 1; 
        // If element is smaller, ignore right half 
        else
            right = middle - 1; 
    } 
    // if element is not present then return -1 
    return -1; 
}
int main()
{
    int a[] = { 10, 12, 20, 32, 50, 55, 65, 80, 99 };
    int element = 12;
    int size = sizeof(a) / sizeof(a[0]); 
    sort(a, a + size);
    int result = BinarySearch(a, 0, size - 1, element); 
    if(result == -1)
        cout<<"Element is not present in array";
    else
        cout<<"Element is present at index "<< result;
    return 0;
}

2) Recursive Method

Piece-wise Code explanation

Consider the above example only
Step 1: Calculate the middle element (50) and compare it with the element we need to search i.e. 12. Since they are not equal and 12 < 50, consider the left sub-array only.

int middle = (left + right) / 2; 
if (sorted_array[middle] == element) 
    return middle; 

Step 2: Since 12<50 we will again make a call to the function. Now our left index remains the same i.e. 0 but our we'll change our right index to middle-1 i.e. 3.
So we will now consider our array from 0-3 only. And we'll search in that.

if (sorted_array[middle] > element) 
    return BinarySearch(sorted_array, left, middle - 1, element); 

Step3: Now since 12 matches with the middle element, it'll return its index to the last call which has been made to this function. And that function will return the index which is 1 to the main function.

if(sorted_array[middle] == element) 
    return middle; 

Full Code

#include <bits/stdc++.h>
using namespace std;
int BinarySearch(int sorted_array[], int left, int right, int element) 
{ 
    if (right >= left) 
    { 
        int middle = (left + right) / 2; 
        // If the element is present at the middle itself 
        if (sorted_array[middle] == element) 
            return middle; 
        // If element < middle, then it can only be present in left subarray 
        if (sorted_array[middle] > element) 
            return BinarySearch(sorted_array, left, middle - 1, element); 
        // Else the element can only be present in right subarray 
        return BinarySearch(sorted_array, middle + 1, right, element); 
    } 
    // We reach here when element is not 
    // present in array 
    return -1;  
} 
int main()
{
    int a[] = { 1, 5, 7, 3, 4, 8, 2, 9, 6 };
    int element = 5;
    int size = sizeof(a) / sizeof(a[0]); 
    sort(a, a + size);
    int result = BinarySearch(a, 0, size - 1, element); 
    if(result == -1)
        cout<<"Element is not present in array";
    else
        cout<<"Element is present at index "<< result;
    return 0;
}

3) STL Function

binary_search(startaddress, endaddress, valuetofind)
The behavior of this function template is equivalent to:

template <class ForwardIterator, class T>
  bool binary_search (ForwardIterator first, ForwardIterator last, const T& val)
{
  first = std::lower_bound(first,last,val);
  return (first!=last && !(val<*first));
}

Returns true if any element in the range [startaddress,endaddress) is equivalent to valuetofind, and false otherwise.

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int a[] = { 10, 12, 20, 32, 50, 55, 65, 80, 99 };
    int element = 12;
    int size = sizeof(a) / sizeof(a[0]); 
    sort(a, a + size);
    if (binary_search(a, a + size, element)) 
        cout << "\nElement found in the array"; 
    else
        cout << "\nElement not found in the array"; 
    return 0;
}

With this article at OpenGenus, you must have the complete idea of implementing Binary Search in C++. Enjoy.