Construct Binary Tree from Inorder and Preorder traversal

In this article at OPENGENUS, we present two approaches to Construct Binary Tree from Inorder and Preorder traversal. We start with background information on constructing Binary Tree from a given traversal or a set of traversals.

Introduction

Why we cannot use only Inorder traversal to construct Binary Tree?

In order to construct a unique binary tree, we cannot rely only on the Inorder Traversal. With only inorder traversal of the binary tree and no more information we may find a binary tree but not a unique binary tree. From the inorder traversal we could pick possibly more than one node as root node. If the tree does not have to be balanced then we could potentially pick any of the node as root node.

Example:
Inorder Traversal : [1,2,3,4,5,6,7,8]

• We can form non-balanced tree by having 1 as root node:

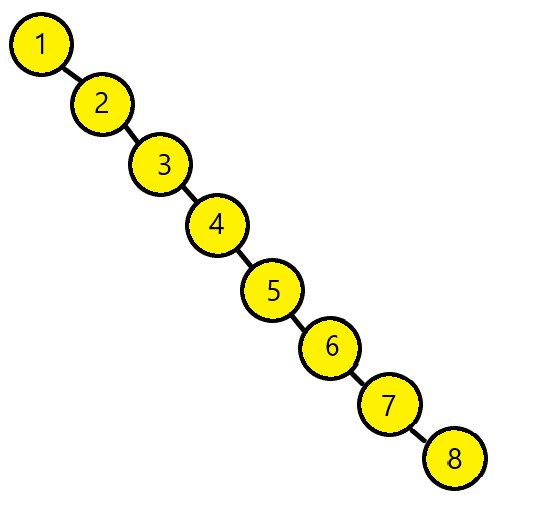
The pre-order traversal of this tree would be [1,2,3,4,5,6,7,8]

• Now, for the same tree we can consider node 4 as root node.
  It would look something like this:
  

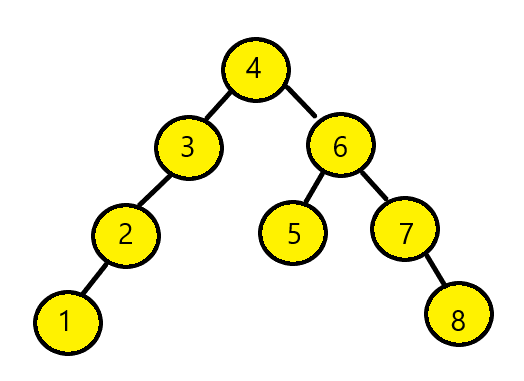
It will have pre-order traversal as [4,3,2,1,6,5,7,8]

Since both the above trees generate the same in-order traversal but different pre-order traversal there is no guarantee for a single,unique binary tree to be formed from the In-order traversal. Hence we need additional traversal information for the tree to be unique.

Inorder + Preorder to Binary Tree

Now, let us construct tree from given Inorder and Preorder Traversals.
Let us assume that the Inorder Sequence is [4, 2, 5, 1, 6, 3]
Preorder Traversal is [1, 2, 4, 5, 3, 6]
Now from the preorder sequence we know that the leftmost element is the root of the tree. That is node 1 is the root of the tree. Now we will search node 1 in inorder sequence and find elements on the left side of root node and those to the right.
From above we know that node 1 is the root node and node 4, 2, 5 are on the left wheras node 6 and 3 on right. Hence we get this:

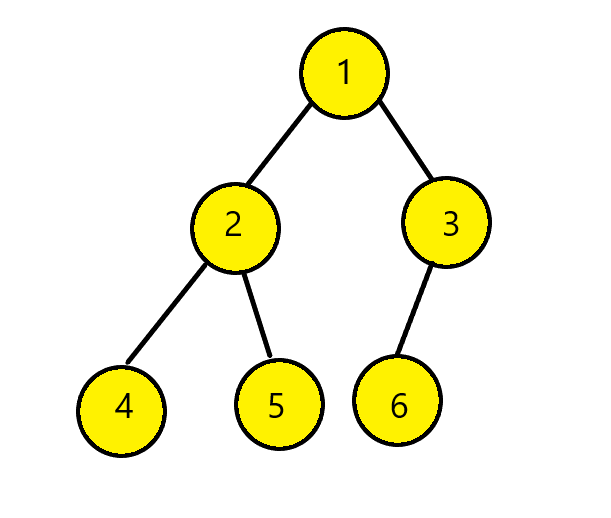
Approach 1

Algorithm:

• Pick element from the preorder and then increment the preorder index variable for next element in next recursive call.
• Create new tree node with data as picked element.
• Find that element index in Inorder traversal.
• Call function again for elements before index of that element and build the left subtree of node.
• Call the function for elements after that element index for right subtree.
• Return the root node.

struct node{
    int val;
    node* right;
    node* left;
}

Now we have the helper function to help us find the index value in array. We will assume the value is present in the inorder traversal.

int helper(char arr[], int start, int end, int value)
{
    int i;
    for (i = start; i <= end; i++)
    {
        if (arr[i] == value)
            return i;
    }
}

Now we define the function maketree, this will be our recursive function to construct the binary tree of size length from Inorder traversal and preorder traversal.

• First we pick the current node from Preorder traversal using the preIndex and increment preIndex
• If that node has no children then we will return
• Else we find the index of this node in Inorder traversal
• Using the index in the Inorder traversal, we will construct the left and right subtree

node* maketree(int in[], int pre[], int istart, int iend)
{
    static int preIndex = 0;
    if (istart > iend)
        return NULL;
    node* finNode = newNode(pre[preIndex++]);
    if (istart == iend)
        return finNode;
    int iIndex = helper(in, istart, iend, finNode->data);
    finNode->left = maketree(in, pre, istart, iIndex - 1);
    finNode->right = maketree(in, pre, iIndex + 1, iend);
 
    return finNode;
}

Time complexity will be O(n^2)

Approach 2:

We can use hashmaps for the above problem as well. We can store the indexes of the inorder traversal in hash table and then we can perfrom our search in O(1) time.

• We start by picking the current node from preorder traversal using the preIndex and increment it
• If the node has no children then we will return
• Else we will find the index of this node in Inorder traversal
• Use the index in Inorder traversal and we will construct the left and right subtree

struct Node* maketree(int in[], int pre[], int istart,
                       int iend, unordered_map<int, int>& mp)
{
    static int preIndex = 0;
    if (istart > iend)
        return NULL;
    int curr = pre[preIndex++];
    struct Node* finNode = newNode(curr);
    if (istart == iend)
        return finNode;
    int inIndex = mp[curr];
    finNode->left = maketree(in, pre, istart, inIndex - 1, mp);
    finNode->right = maketree(in, pre, inIndex + 1, iend, mp);
    return finNode;
}

Time complexity: O(n)

Construction of the binary tree from Inorder and Postorder Traversal

Example:
Inorder Traversal: [4, 2, 5, 1, 3]
Postorder Traversal: [4, 5, 2, 3, 1]
Now from the postorder traversal we can see the right most element, node 1 is the root node. From Inorder traversal we can see that node 3 is on right of root node 1, and others on left. In similar fashion, we end up with tree:

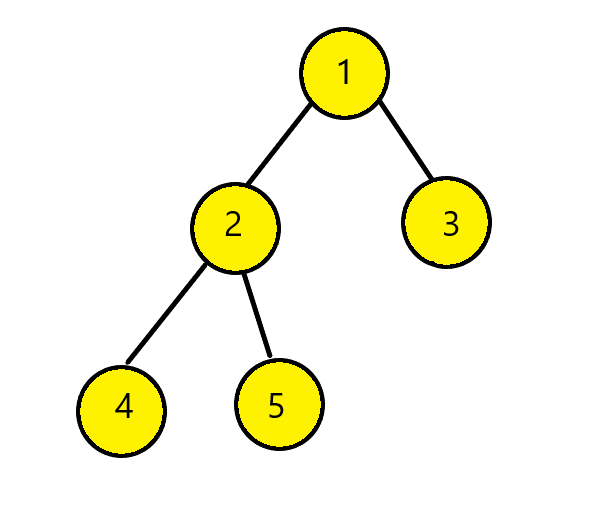
For the construction of the binary tree from the inorder traversal and postorder traversal, we can use the same concept as used in above approaches to find our tree.
By using both recursion and hashmaps we will be able to re-construct our tree from the traversals.