Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 5 minutes
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involving recursively-defined objects.
They are named after the Belgian mathematician Eugène Charles Catalan (1814–1894).
The Catalan numbers are:
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, ...
Cn represesnts the nth Catalan Number
Note: Nth Catalan Number can be mathematically represented by

Some alternate expressions worth mentioning are :
- Recurrence Form:

- Asymptotic Growth:

- Intergral Representation

Sample Calculation
Let us calculate the 4th Catalan number
4th Catalan number is denoted by Catalan(4)
Let us follow the basic definition
Catalan(4) = 1/(4+1) * C(8,4) (Where C(8,4) is the selection of 4 events out of 8)
Catalan(4) = (1/5) * (8! / (4! * 4!))
Catalan(4) = 0.2 * 70
Catalan(4) = 14
Therefore, the 4th Catalan number is 14.
Algorithm
The nth Catalan Number (Cn) can be calculated by essentially one formula (as mentioned above) but the approaches can be different. I will be discussing three methods to find nth Catalan Number. All of them would rely mostly on combinatorial mathematics along with array and recurrence utilisation.
Calculating Catalan Numbers using Recursive Solution
This method utilizes the power of recursive computation and is a lot easier to manipulate. The basic Mathematical concept behind this algorithm is :

Using this methid, to calculate the n th catalan number, one needs to calculate all previous catalan numbers.
function C(n){
if n <= 1
return 1
SUMMATION = 0
increment i from 1 to n {
SUMMATION += C(i) * C(n-i-1)
}
return SUMMATION
}
Calculating Catalan Numbers using Dynamic Programming
In the recursive implementation, a lot of repetitive work is done. Acknowledging this, the programming technique of Dynamic Programming also offers a solution for this problem.
Thus, we calculate previous catalan numbers only once.
function C(n){
unsigned long int array[n+1]
array[0] = array[1] = 1
iterate i from 2 to n{
array[i] = 0
iterate j from 0 to i{
array[i] = array[j] * array[i-j-1];
}
}
return array[n]
}
Calculating Catalan Numbers using Simple Definition Approach
We can use the intial definition to get the solution for this problem. One can simply find the combination of 2n objects among which n are to be selected and use that. It gives you the best performance for large test cases.
function combinatoric(a){
//returns (C(2n,n))
}
function C(n){
return ((1/(n+1))*combinatoric(n))
}
Complexity
- For Recursive Function:
Θ(N ^ 2) - For Dynamic Programming:
Θ(N ^ 2) - For Simple Definition Aprroach:
Θ(N)
Implementations
Implementations of the various techniques of calculating Catalan number in various languages.
- Recursive-python
- Dynamic-python
- Combinatoric-python
- Recursive-C
- Combinatoric-JS
- Dynamic-Ruby
- Dynamic-C++
- Java
- Scala
Recursive-python
# Part of Cosmos by OpenGenus Foundation
def catalan(n):
if n <=1 :
return 1
res = 0
for i in range(n):
res += catalan(i) * catalan(n-i-1)
return res
for i in range(10):
print(catalan(i), emd=" ")
Dynamic-python
# Applying Dynamic Programming to give Cn
def Catalan(n):
if n == 0 or n == 1:
return 1
c_nums = [0 for i in range(n+1)]
c_nums[0] = 1
c_nums[1] = 1
for i in range(2, n+1):
c_nums[i] = 0
for j in range(i):
c_nums[i] = c_nums[i] + c_nums[j] * c_nums[i-j-1]
return c_nums[n]
# Testing Utility
for i in range(10):
print (Catalan(i))
Combinatoric-python
def catalanNum(n):
if n <=1 :
return 1
result = 0
for i in range(n):
result += catalanNum(i) * catalanNum(n-i-1)
return result
for i in range(15):
print(catalanNum(i))
Recursive-C
/* Part of Cosmos by OpenGenus Foundation. */
#include <stdio.h>
/*
* Returns value of Binomial Coefficient C(n, k).
*/
unsigned long int
binomial_Coeff(unsigned int n, unsigned int k)
{
unsigned long int res = 1;
int i ;
/* Since C(n, k) = C(n, n-k) */
if (k > n - k)
k = n - k;
/* Calculate value of nCk */
for (i = 0; i < k; ++i) {
res *= (n - i);
res /= (i + 1);
}
return (res);
}
/*
* A Binomial coefficient based function to find nth catalan
* O(n) time Solution.
*/
unsigned long int
catalan(unsigned int n)
{
/* Calculate value of 2nCn */
unsigned long int c = binomial_Coeff(2 * n, n);
/* return 2nCn/(n+1) */
return (c / (n+1));
}
/* Driver program to test above functions. */
int
main()
{
unsigned int n;
printf("Input n \nNth Catalan you want :");
scanf("%d", &n);
printf("Nth Catalan number is: %lu", catalan(n));
return (0);
}
Combinatoric-JS
function binomial_Coeff(n, k) {
let res = 1;
if (k > n - k) {
k = n - k;
}
for (let i = 0; i < k; i++) {
res *= (n - i);
res /= (i + 1);
}
return res;
}
function catalan(n) {
const c = binomial_Coeff(2 * n, n);
return c / (n + 1);
}
for (let j = 0; j < 10; j++) {
console.log(catalan(j));
}
Dynamic-Ruby
def catalan(num)
return 1 if num <= 1
ans = 0
i = 0
while i < num
first = catalan i
second = catalan num - i - 1
ans += (first * second)
i += 1
end
ans
end
Integer x = 1
while x <= 10
res = catalan x
puts res
x += 1
end
Dynamic-C++
#include <iostream>
using namespace std;
// Part of Cosmos by OpenGenus Foundation
int main()
{
int n;
cin >> n;
long long cat[100000];
cat[0] = 1;
cout << cat[0];
for (int i = 1; i <= n; i++)
{
cat[i] = 2 * (4 * i + 1) * cat[i - 1] / (i + 2);
cout << cat[i] << endl;
}
}
Java
// Part of Cosmos by OpenGenus Foundation
import java.util.HashMap;
import java.util.Map;
public class CatalanNumber {
private static final Map<Long, Double> facts = new HashMap<Long, Double>();
private static final Map<Long, Double> catsI = new HashMap<Long, Double>();
private static final Map<Long, Double> catsR1 = new HashMap<Long, Double>();
private static final Map<Long, Double> catsR2 = new HashMap<Long, Double>();
static{//pre-load the memoization maps with some answers
facts.put(0L, 1D);
facts.put(1L, 1D);
facts.put(2L, 2D);
catsI.put(0L, 1D);
catsR1.put(0L, 1D);
catsR2.put(0L, 1D);
}
private static double fact(long n){
if(facts.containsKey(n)){
return facts.get(n);
}
double fact = 1;
for(long i = 2; i <= n; i++){
fact *= i; //could be further optimized, but it would probably be ugly
}
facts.put(n, fact);
return fact;
}
private static double catI(long n){
if(!catsI.containsKey(n)){
catsI.put(n, fact(2 * n)/(fact(n+1)*fact(n)));
}
return catsI.get(n);
}
private static double catR1(long n){
if(catsR1.containsKey(n)){
return catsR1.get(n);
}
double sum = 0;
for(int i = 0; i < n; i++){
sum += catR1(i) * catR1(n - 1 - i);
}
catsR1.put(n, sum);
return sum;
}
private static double catR2(long n){
if(!catsR2.containsKey(n)){
catsR2.put(n, ((2.0*(2*(n-1) + 1))/(n + 1)) * catR2(n-1));
}
return catsR2.get(n);
}
public static void main(String[] args){
for(int i = 0; i <= 15; i++){
System.out.println(catI(i));
System.out.println(catR1(i));
System.out.println(catR2(i));
}
}
}
Scala
object Catalan {
def number(n: Int): BigInt = {
if (n < 2) {
1
}
else {
val (top, bottom) = (2 to n).foldLeft((BigInt(1), BigInt(1))) {
case ((topProd: BigInt, bottomProd: BigInt), k: Int) => (topProd * (n + k), bottomProd * k)
}
top / bottom
}
}
// to test
// var c = catalan(3)
// println(c)
def recursive(n: Int): Int = {
if (n <= 1) 1
else (0 until n).map(i => recursive(i) * recursive(n - i - 1)).sum
}
}
object Main {
def main(args: Array[String]): Unit = {
for (n <- 0 until 20) {
println(s"${n}: ${Catalan.number(n)}")
}
}
}
Applications
The applications of Catalan Numbers are quite evident in various fields of studies. I will be dicussing a few of them in the field of Combinatorics.
- Cn is the number of Dyck words of length 2n. A Dyck word is a string consisting of n X's and n Y's such that no initial segment of the string has more Y's than X's. For example, the following are the Dyck words of length 6:
A modified version of this issue is also known as the bracket problem - in which we have to match opened and closed parenthesis- which many might've come across in problem solving using stacks
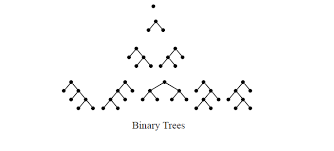
- Successive applications of a binary operator can be represented in terms of a full binary tree. (A rooted binary tree is full if every vertex has either two children or no children.) It follows that Cn is the number of full binary trees with n + 1 leaves:

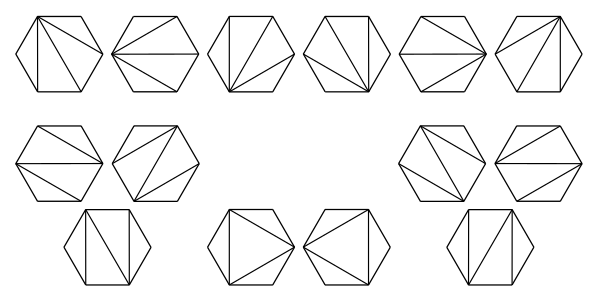
- A convex polygon with n + 2 sides can be cut into triangles by connecting vertices with non-crossing line segments (a form of polygon triangulation). The number of triangles formed is n and the number of different ways that this can be achieved is Cn. The following hexagons illustrate the case n = 4:
-
In chemical engineering Cn-1 is the number of possible separation sequences which can separate a mixture of n components.
-
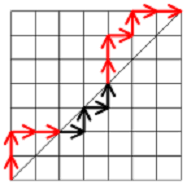
Dyck Paths are also field of application for the Catalan Numbers. A Dyck path is a series of equal length steps that form a stariway walk from (0,0) to (n,n) that will lie strictly below, or touching the diagonal x=y.
Clearly, each acceptable route is either above the diagonal or below the diagonal and both of these paths are symmetric. So we calculate the number of paths below the diagonal and multiply it by 2. Each route is a sequence of n northernly blocks n westernly blocks. We can gather the conclusion that number of acceptable routes above the diagonal equals the nth Catalan Number
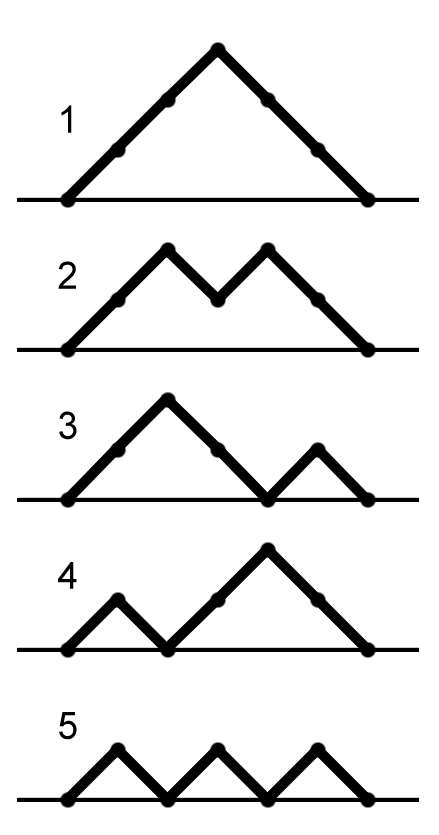
- Binary trees: A rooted binary tree is a tree with one root node, where each node has either zero or two branches descending from it. A node is internal if it has two nodes coming from it. How many rooted binary trees are there with n internal nodes? Yes, they are nth Catalan Numbers
- Determining Monotonic Lattice Paths. They can be straight away calculated by the usage of Catalan Numbers! The number of paths from (0,0) to (n,n) which crosses XY line are also equal to Cn!