Check if a Binary Tree is skewed or not

There are two types of skewed binary trees: Left and Right skewed binary trees. From their characteristics we can conclude that they either have one child node or no node at all.

Hence, below given binary tree is skewed.

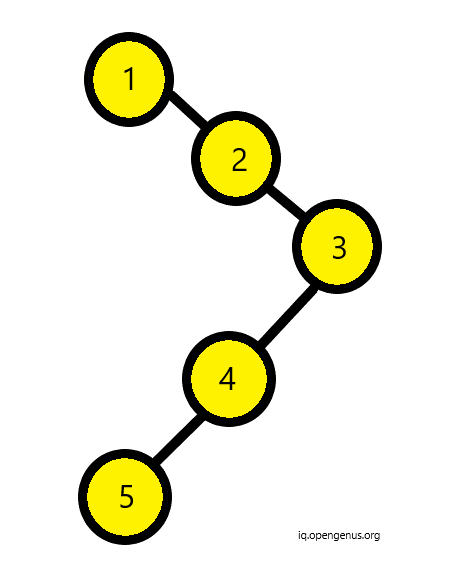
and below binary tree is not skewed since one of its nodes have two child nodes.

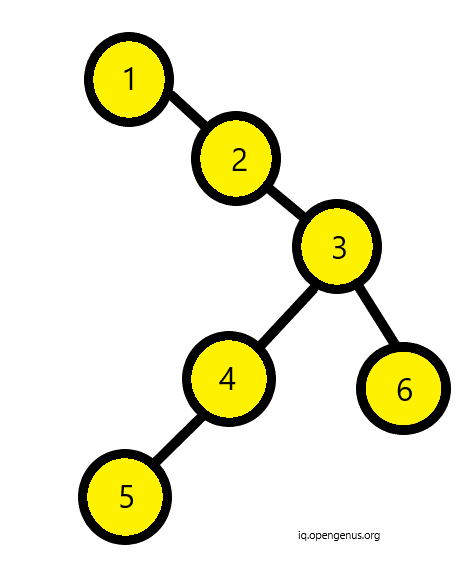
Hence, in its implementation we will recursively check if the nodes of the binary tree have one child nodes or no node. If so, then we will keep traversing else return false on encountering two child nodes.

Algorithmic Steps:

• For each node N, check the following:
• If both left and right child nodes are present, it is not a valid skewed tree.
• If the node has only one left child node then we check its left child node
• If the node has only one right child node then we check its right child node
• If there are no child nodes, it is a valid node of a skewed tree.

The pseudocode is as follows:

skewed(node* root) 
{ 
    //This condition checks if the given is null node or leaf node
    if (root == NULL || (root->left == NULL &&  
                        root->right == NULL)) 
        return true; 
  
    //Now, we check if the node has two children, if yes then we return false 
    if (root->left && root->right)  
        return false; 
        
    //If the node has only one left child node then we check its left child node 
    //else we check its right root node
    if (root->left) 
        return skewed(root->left); 
    return skewed(root->right); 
} 

Following is the complete implementation in C++ with the node definition and a function to create a new node:

//definition of a node
struct node{
    int value;
    struct node *left,*right;
}
//function to make new node
node* newnode(int value){
    node* t = new node;
    t->value = value;
    t->left = t->right = Null;
    return(t);
}

bool skewed(node* root) 
{ 
    //This condition checks if the given is null node or leaf node
    if (root == NULL || (root->left == NULL &&  
                        root->right == NULL)) 
        return true; 
  
    //Now, we check if the node has two children, if yes then we return false 
    if (root->left && root->right)  
        return false; 
        
    //If the node has only one left child node then we check its left child node 
    //else we check its right root node
    if (root->left) 
        return skewed(root->left); 
    return skewed(root->right); 
} 

Explanation:

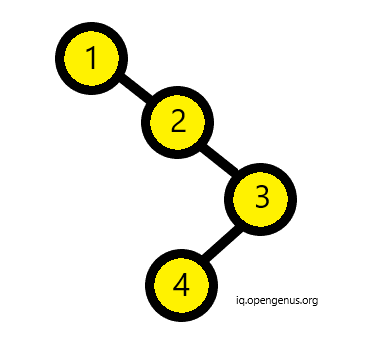
• Consider the above binary tree. Firstly, the function will check if the root is null or if both left and right nodes are null. In above binary tree, initially this condition is false.
• Now, it checks if the right and the left nodes are not null. If so, it will return false since skewed binary tree can only have one child either on left or right. In above binary tree it is not the case.
• Now, we come for the last condition. If the left node is not null then it returns recursively the left node of the root. Else, in similar recursive fashion it returns the right node of root.
• This way in above example, the leaf node will satisfy first condition of null left and null right node and hence return true. Hence, its a skewed binary tree.
• If the tree would not have been skewed then the function would have returned false.

Time Complexity

Best Case : O(1) if the root has two children
Worst Case : O(k) if the tree is skewed where k is the height of tree

Happy Coding!