Convert a Binary Tree to a Skewed Binary Tree

A simple binary tree can be easily converted into a skewed binary tree. Since we know, the skewed binary tree can be of two types:

• Left Skewed Binary Tree
• Right Skewed Binary Tree

Hence, we can easily convert any binary tree into skewed binary tree.

We can convert binary tree into two types of skewed binary trees:

• Increasing Skewed Binary Trees
• Decreasing Skewed Binary Trees

Consider a binary tree:

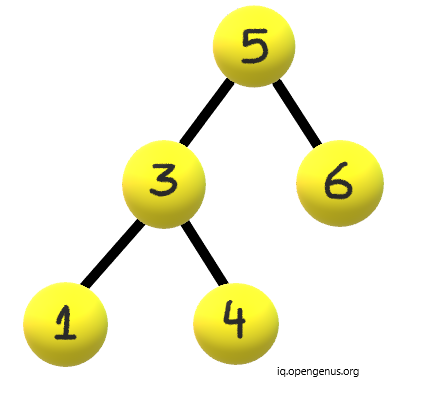
Case 1 : Increasing Order

• We will do inorder traversal, as inorder traversal of a Binary Search Tree provides us increasing sequence of values of nodes.
• Using above logic, the left node traversal will give us smaller values.
• Then after traversal of left subtree, we will add previous node of skewed tree to our root node.
• For the larger values, now we traverse the right subtree.

The Increasing skewed binary tree will be:

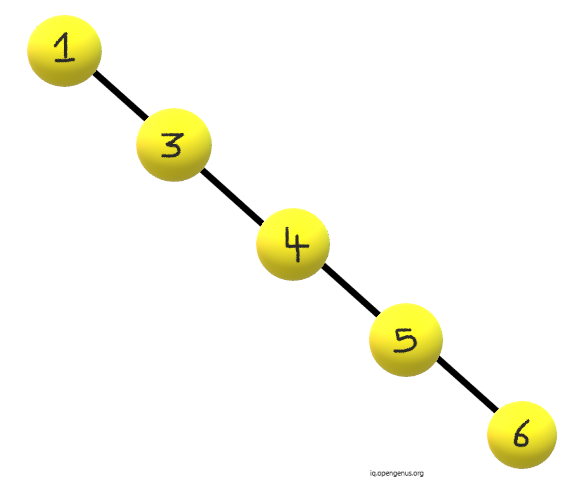
Following is the pseudocode for Increasing order (case 1):

void skewed(node *root)
{
    // Base Case
    if (!root)
        return;
 
    // To check the order in which the skewed tree should be made
    skewed(root->right);
 
    node *rightNode = root->right;
    node *leftNode = root->left;
 
    // To check if the root Node of the skewed tree is not defined
    if (!headNode)
    {
        headNode = root;
        root->left = NULL;
        prevNode = root;
    }
    else
    {
        prevNode->right = root;
        root->left = NULL;
        prevNode = root;
    }
 
    // Now we will Recurse for the left or right subtree on the basis of the order
    skewed(leftNode);
}

Case 2 : Decreasing Order

• Recursion of the right node will be done first in order to get larger values first.
• Then we will connect the root node after the previous node.
• At the end we traverse the left subtree for smaller values since the tree should be skewed in decreasing order.

The decreasing skewed binary tree will be:

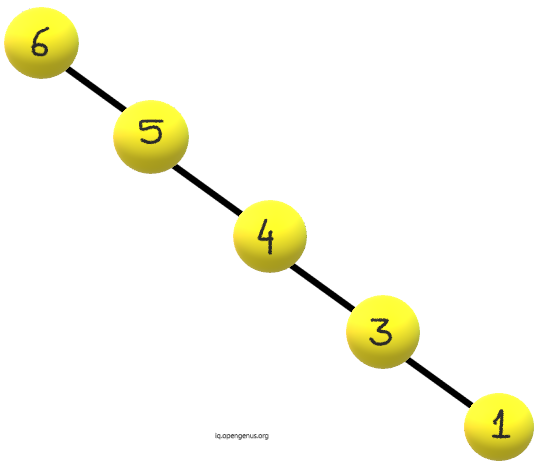
The pseudocode will be as follows:

void skewed(node *root)
{
    // Base Case
    if (!root)
        return;
 
    // To check the order in which the skewed tree should be made
    skewed(root->left);
 
    node *rightNode = root->right;
    node *leftNode = root->left;
 
    // To check if the root Node of the skewed tree is not defined
    if (!headNode)
    {
        headNode = root;
        root->left = NULL;
        prevNode = root;
    }
    else
    {
        prevNode->right = root;
        root->left = NULL;
        prevNode = root;
    }
 
    // Now we will Recurse for the left or right subtree on the basis of the order
    skewed(rightNode);
}

Both the functions for Increasing and Decreasing order can be merged together using a control variable K where:

• K = 1 for Increasing order
• K = 0 for Decreasing order

We have presented the merged function skewed(node, K) accordingly.

Implementation of our nodes:

//definition of a node
struct node{
    int value;
    struct node *left,*right;
}
//function to make new node
node* newnode(int value){
    node* t = new node;
    t->value = value;
    t->left = t->right = Null;
    return(t);
}

Final implementation can be done as follows:

void skewed(node *root, int k)
{
    // Base Case
    if (!root)
        return;
 
    // To check the order in which the skewed tree should be made
    if (k)
        skewed(root->right, k);
    else
        skewed(root->left, k);
 
    node *rightNode = root->right;
    node *leftNode = root->left;
 
    // To check if the root Node of the skewed tree is not defined
    if (!headNode)
    {
        headNode = root;
        root->left = NULL;
        prevNode = root;
    }
    else
    {
        prevNode->right = root;
        root->left = NULL;
        prevNode = root;
    }
 
    // Now we will Recurse for the left or right subtree on the basis of the order
    if (k)
        skewed(leftNode, k);
    else
        skewed(rightNode, k);
}

Explanation:

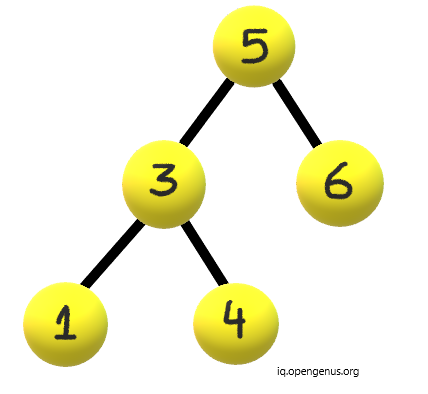
• In above tree, the function will start by checking if root is null. If so then it will return. This is not the case with our example.
• If k is 1, that means we need to follow increasing order. Hence we will recursively call the right child of root and pass k as argument to keep the track if we need to find increasing or decreasing order of skewed binary tree.
• Then, we make a new node for the final skewed tree. We initialise the left node with left child of root and right with right child of node.
• If the root of the skewed binary tree is not defined then we define the headnode and right node of skewed tree as root. The left node is defined null since its a skewed binary tree and it can only have one child.
• If headnode is already defined then the right child of previous node is given value of our root and left child is null since in skewed tree, one node can have only one child. Previous node is given value of root.
• At the end we recurse according to our value of k that defines if the order will be increasing or decreasing.
• If k is 1 then we recursively call function and pass left node as argument else we will pass right node if k = 0.

Happy Coding!