Checking if a Binary Tree is foldable

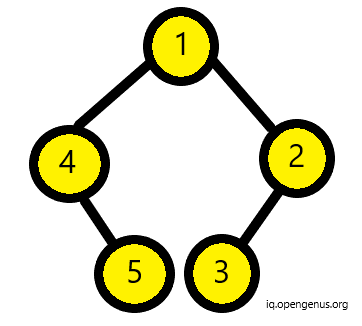
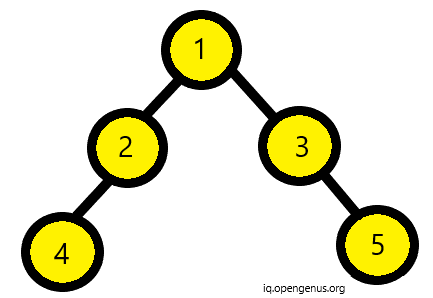
A binary tree is foldable if the left subtree and right subtree are mirror images of each other. An empty tree is also foldable. Below binary trees are foldable since both have a left subtree that is the mirror image of right subtree.

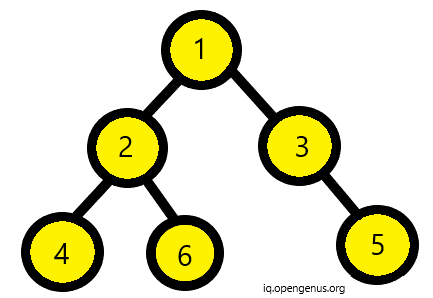
However, below binary tree is not foldable.

We can check if a binary tree is foldable or not in two ways:

• By changing the left subtree to its mirror equivalent. Then checking if the mirror is equivalent to te right subtree.
• Compare and check if right and left subtrees are mirrors of each other

Algorithm for Method 1:

• If tree is empty, return true.
• Convert left subtree to mirror image.
• If the right subtree is equivalent to mirror image then return true else return false.

//definition of a node
struct node{
public:
    int val;
    node* left;
    node* right;
};

Below is the mirror function:

• If the node is null then we will return.
• Else, first we traverse the left subtree in recursive fashion then the right subtree.
• We will swap the left and right node pointers.

void Mirror(node* Node)
{
    if (Node == NULL)
        return;
    else {
        node* temp;
        Mirror(Node->left);
        Mirror(Node->right);

        temp = Node->left;
        Node->left = Node->right;
        Node->right = temp;
    }
}

Below is the same function that checks if the structure is same or not:

• If both a and b are null then return true.
• If a and b are not null and both left and right nodes of both a and b are null then return true.
• Else return false.

bool same(node* a, node* b)
{
    if (a == NULL && b == NULL) {
        return true;
    }
    if (a != NULL && b != NULL && 
    same(a->left, b->left) &&
    same(a->right, b->right)) {
        return true;
    }
 
    return false;
}

The next function is foldable function:

• Here first we declare a boolean variable res.
• Then if root is null then return true.
• Then we call mirror function defined above for left subtree.
• Then in res we store the result of function same we defined above.
• Then we again recursively call the left node as argument in Mirror function.
• Return res.

bool foldable(node* root)
{
    bool res;
    if (root == NULL)
        return true;
    Mirror(root->left);
    res = same(root->left, root->right);
    Mirror(root->left);
    return res;
}

Algorithm for Method 2:

In function check(a,b):

• Check if both trees are empty then return true.
• If only one of them is empty then return false.
• If one subtree is mirror of other then return true.

bool check(node* n1, node* n2)
{
    if (n1 == NULL && n2 == NULL) {
        return true;
    }
    if (n1 == NULL || n2 == NULL) {
        return false;
    }
    return check(n1->left, n2->right)
           && check(n1->right, n2->left);
}

In function foldable(a):

• First we will check if the trees are null then return true.
• Else check if the left and right subtree are the mirror of each other using the check function defined above.

bool foldable(node* root)
{
    if (root == NULL) {
        return true;
    }
 
    return check(root->left, root->right);
}

Using both above approaches we can easily find if a binary tree is foldable or not.
Happy Coding!