Children sum parent in a Binary Tree

In this article, I will be discussing about the problem "Children sum parent in a Binary Tree" in detail:

Contents:

• Introduction
• Optimized approach
• Implementation
• Time and Space Complexity Analysis

Introduction:

In this problem at OpenGenus, we are going to check whether the value of each node of a binary tree is equal to sum of value of its left child and right child. we will consider each leaf node satisfies the property of children sum parent.

Example 1:

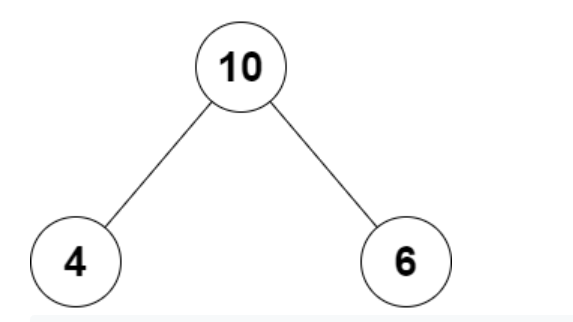
In this example, we can see that the value of root node is 10 and the sum of the value of its left child and right child is 4+6 = 10. Since, the value of the root node and sum of its left child sub-tree and right child sub-tree are equal, therefore it satisfies the children sum parent property.

Example 2:

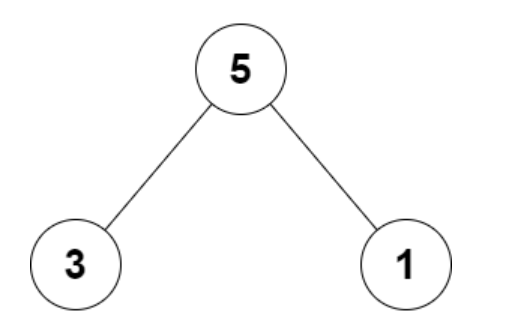
In this example, we can see that the value of root node is 5 and the sum of the value of its left child and right child is 3+1 = 4. Since, the value of the root node and sum of its left child sub-tree and right child sub-tree are not equal, therefore it does not satisfies the children sum parent property.

Optimized Approach:

In the optimized approach, we will traverse the given binary tree. For each node check (recursively) if the node and both its children satisfy the Children Sum Property or not, if so then we will return 1 else return 0. we will follow the following steps to check weather the given binary tree is satisfying the children sum property or not.

1. We will create a function isSumProperty() and pass the root node as a parameter in this.
2. If the given binary tree satisfies the children sum parent property then the above function return 1, otherwise it will return 0.
3. If the root is null or is a leaf node,then we will return 1.
4. We will traverse the binary tree recursively and for each node we will calculate the sum of its left child and right child.
5. If the calculate sum is equals to the value of its root node then we will check for its left subtree and right subtree.
6. If the calculated sum is not equals to the value of its root node then we will return 0.

Implementation:

import java.util.*;
class Node{
	int data;
	Node left,right;
	
	Node(int key)
	{
	    data = key;
	    left = right = null;
	}
}
class Tree
{
    //Function to check whether all nodes of a tree have the value 
    //equal to the sum of their child nodes.
    public static int isSumProperty(Node root)
    {
        // add your code here
        if(root==null){
            return 1;
        }
        if(root.left==null && root.right==null){
            return 1;
        }
        int sum = 0;
        if(root.left!=null){
            sum+= root.left.data;
        }
        if(root.right!=null){
            sum+=root.right.data;
        }
        
        if(root.data==sum){
            return isSumProperty(root.left)*isSumProperty(root.right);
        }
        return 0;
        
    }
    public static void main (String[] args)
    {
        Node root = new Node(15);
        root.left = new Node(16);
        root.left.right = new Node(67);
        root.left.right.left = new Node(44);
        root.left.left = new Node(8);
        root.left.left.left = new Node(55);
        root.right = new Node(17);
        root.right.right = new Node(41);
        root.right.left = new Node(7);
        root.right.left.right = new Node(11);
        System.out.print(isSumProperty(root));
    }
}

Example:
Let's take example of a binary tree of level 3 and check if it satisfies children sum property:

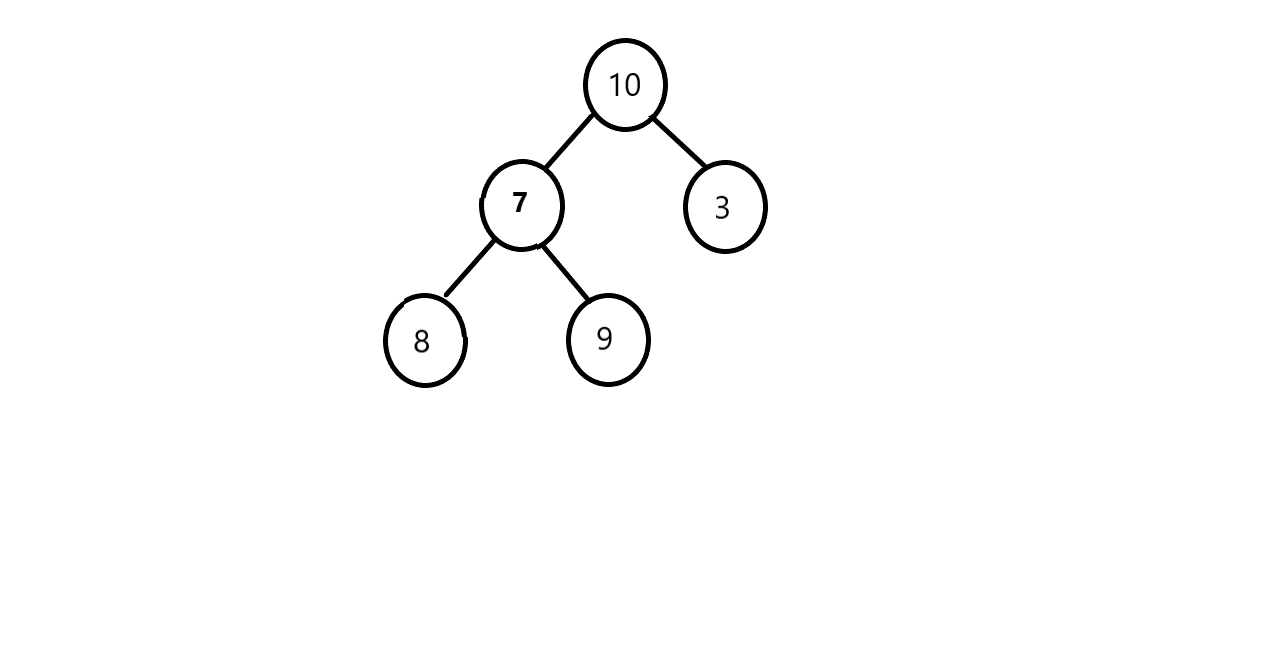
According to our code,

1. First we will check if the root node of the given binary is null or is a leaf node. Here it is not null and also not a leaf node.
2. So, in the next step we will add the value of left child and right child and store it in the value of sum. Here in this example the value of sum will be 7+3 = 10.
3. Since the value of sum is equal to the root node so, we will recursively check for the left sub-tree and then for the right sub-tree.
4. In the next step the function call for the left sub-tree will in the call stack. Similarly, in that function firstly, we will check if it is null or a leaf node. Here in this example the node is neither null nor leaf node.
5. So, in the next step we will create a variable sum and add the values of left-child and right-child and store it in the value of sum.
6. Since, in this example the value of sum will be 17 and is not equal to the value of node. so, we will return 0 to its above function call and the above function call will also return 0.

Time and Space Complexity Analysis:

The time complexity of the above solution will be O(N),where N is total number of nodes in the binary tree. As in the above approach we are doing complete traversal of the binary tree, so the overall complexity of the above solution will be O(N).

The space complexity of the above solution will be O(H), where H is the height of the tree. As we know the right sub-tree call will not execute till the left sub-tree call has completed its execution, so at a time there will be atmost H function calls in the call stack.

With this article at OpenGenus, you must have the complete idea of Children sum parent in a Binary Tree problem.