Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

A cuckoo filter is a probabilistic data structure that is used to test whether an element is a member of a set or not. It is similar to Bloom filter. It can show false positives but not false negatives. It can also delete existing items.

It is a hash table that uses cuckoo hashing to resolve collisions. It decreases the space used by only maintaining a fingerprint of the value to be stored in the set. It uses a small f-bit fingerprint to store the data. The value of f is decided by the ideal false positive rate.

The false-positive rate is the probability that a false alarm will be raised. Even though the true value is negative it will give a positive result. It is calculated as FP/(FP+TN), where FP is the number of false positives and TN is the number of true negatives.

Table of Contents:

Buckets in cuckoo filter
Cuckoo hashing in cuckoo filter
Insertion operation in cuckoo filter
Lookup function in cuckoo filter
Delete operation in cuckoo filter
Implementing cuckoo filter
Time & Space complexity of Cuckoo Filter
Advantages of Cuckoo filter over Bloom filter
Limitations of Cuckoo Filter

Buckets in cuckoo filter

Cuckoo filter stores the fingerprint of the value to be stored in an array of buckets. The number of fingerprints that a bucket can hold is referred to as b. They have a load that describes the percentage of the filter they are currently using and plays a key role in deciding when cuckoo filter size should be resized. It uses the semi-sort technique. The semi-sort technique can compress the buckets by sorting the fingerprints present in them.

output-onlinepngtools

Cuckoo hashing in cuckoo filter

The cuckoo filter uses cuckoo hashing to resolve collisions. Cuckoo hashing is a method used to avoid collisions in a hash table. It got its name because of its similarities with cuckoo. As a chick of cuckoo pushes the other eggs out of the nest to make a place of their own. Similarly in cuckoo hashing, to insert a new key into the hash table we push the older key to a new place. Though cuckoo filter is based on cuckoo hashing, they use a derivative called partial-key cuckoo hashing.
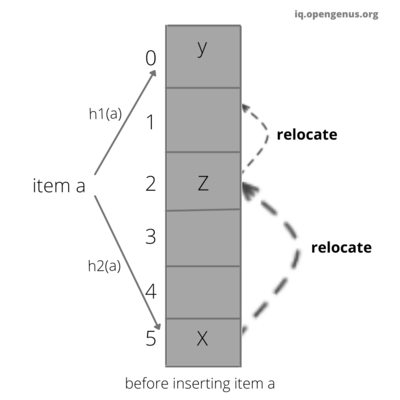
Add-a-subheading-2-
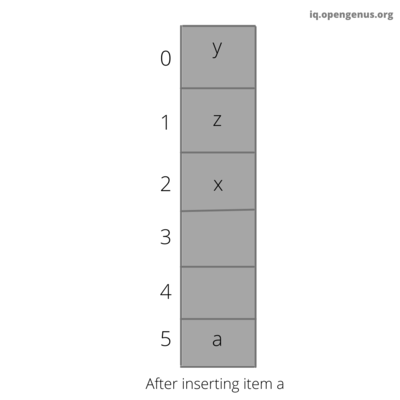
Add-a-subheading-1--1

Insertion operation in cuckoo filter

This function is used to insert the value to be stored into the cuckoo filter. It uses cuckoo hashing to insert the value.

Algorithm implementing insertion in the cuckoo filter.

Step 1: compute the fingerprint of the value to be stored and store it in a variable called fprint.
Step 2: Compute the hash of k(value to be stored), h(k) = k_h using the first hash function and store it in a variable called first_bucket.
Step 3: Compute the hash of fprint,h(fprint)=k_f
Step 4: Xor first_bucket and hash of fprint and store it in a variable called second_bucket.
Step 5: If first_bucket is empty then insert the fprint in bucket[first_bucket].
Step 6: If first_bucket is not empty then insert the fprint in bucket[second_bucket].
Step 7: If second_bucket is not empty then reallocate the entry present in the second_bucket to empty space and insert the fprint in bucket[second_bucket].

Pseudocode of insertion function.

Insert(x){
fprint=fingerprint(x);
first_bucket=hash(x);
second_bucket=first_bucket⊕hash(fprint);
if bucket[first_bucket] or bucket[second_bucket] has an empty entry then
    add fprint to that bucket;
    return Done;

//the two buckets are not empty so we must relocate existing items;
i=randomly pick first_bucket or second_bucket;
for n=0;n<MaxNumKicks;n++ do
    randomly select an entry e from bucket[i];
    swap fprint and the fingerprint stored in entry e;
    i=i⊕hash(fprint);
    if bucket[i] has an empty entry then 
        add fprint to bucket[i];
        return Done;
        
//Hashtable is considered full;
return Failure;
}

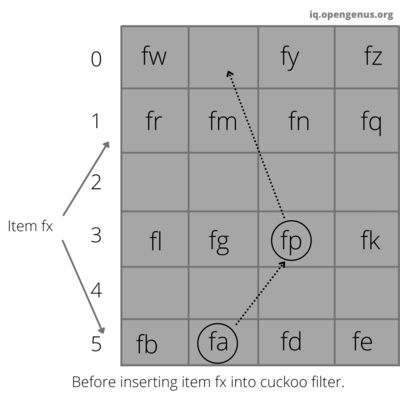
Add-a-subheading-3-

Add-a-subheading-4-

Lookup function in cuckoo filter

Lookup function checks if the given value is present in the cuckoo filter or not. We will compute first_bucket and second_bucket and we will check if the fingerprint of the given value is present in the first_bucket or the second_bucket then it will return true else return false.

Algorithm implementing lookup in the cuckoo filter.

Pseudocode of lookup function.

Lookup(x){
fprint=fingerprint(x);
first_bucket=hash(x);
second_bucket=first_bucket⊕hash(fprint);
if bucket[first_bucket] or bucket[second_bucket] has fprint then 
    return True;
return False;

Delete operation in cuckoo filter

Delete function removes a copy of the fingerprint of the given value from the bucket. We will compute first_bucket and second_bucket and we will check if the fingerprint of the given value is present in the first_bucket or the second_bucket then we will remove a copy of fprint from this bucket.

Algorithm implementing delete in the cuckoo filter.

Step 1: compute the fingerprint of the value to be stored and store it in a variable called fprint.
Step 2: Compute the hash of k(value to be stored), h(k) = k_h using the first hash function and store it in a variable called first_bucket.
Step 3: Compute the hash of fprint,h(fprint)=k_f
Step 4: Xor first_bucket and hash of fprint and store it in a variable called second_bucket.
Step 5: If bucket[first_bucket] or bucket[second_bucket] contains fprint then remove a copy of fprint from this bucket.

Pseudocode of Delete function.

Delete(x){
fprint=fingerprint(x);
first_bucket=hash(x);
second_bucket=first_bucket⊕hash(fprint);

if bucket[first_bucket] or bucket[second_bucket] has fprint then
    remove a copy of fprint from this bucket;
    returnTrue;
return False;

Implementing cuckoo filter

Following is the implementation of Cuckoo Filter in GoLang:

Go


    package main


import (
	"bytes"
	"encoding/binary"
	"errors"
	"fmt"
	"math"
	"crypto/sha1"
	"math/rand"
)


type bucket []fingerprint
type fingerprint []byte
var hasher = sha1.New()
const retries = 200 // how many times do we try to move items around?


type Cuckoo struct {
	buckets []bucket
	m       uint // buckets
	bucket_entries       uint // entries per bucket
	fingerprint_length       uint // fingerprint length
	n       uint // filter capacity
}


func hash(data []byte) []byte {
	hasher.Write([]byte(data))
	hash := hasher.Sum(nil)
	hasher.Reset()
	return hash
}


func nextPower(i uint) uint {
	i--
	i |= i >> 1
	i |= i >> 2
	i |= i >> 4
	i |= i >> 8
	i |= i >> 16
	i |= i >> 32
	i++
	return i
}


func fingerprintLength(b uint, e float64) uint {
	f := uint(math.Ceil(math.Log(2 * float64(b) / e)))
	f /= 8
	if f < 1 {
		return 1
	}
	return f// if f is greater than or equal to 1 return f.
}


// n = len(items), fp = false positive rate
func NewCuckoo(n uint, fp float64) *Cuckoo {
	bucket_entries := uint(4)
	fingerprint_length := fingerprintLength(bucket_entries, fp)
	m := nextPower(n / fingerprint_length * 8)
	buckets := make([]bucket, m)
	for i := uint(0); i < m; i++ {
		buckets[i] = make(bucket, bucket_entries)
	}
	return &Cuckoo{
		buckets: buckets,
		m:       m,
		bucket_entries:  bucket_entries,
		fingerprint_length:   fingerprint_length,
		n:       n,
	}
}


// nextIndex returns the next index for entry, or an error if the bucket is full
func (b bucket) nextIndex() (int, error) {
	for i, f := range b {
		if f == nil {
			return i, nil
		}
	}
	return -1, errors.New("bucket full")
}


// hashes returns h1, h2 and the fingerprint
func (c *Cuckoo) hashes(data string) (uint, uint, fingerprint) {
	h := hash([]byte(data))
	fprint := h[0:c.fingerprint_length]
	first_bucket := uint(binary.BigEndian.Uint32(h))
	second_bucket := first_bucket^ uint(binary.BigEndian.Uint32(hash(fprint)))
	return first_bucket, second_bucket, fingerprint(fprint)
}


func (b bucket) contains(f fingerprint) (int, bool) {
	for i, x := range b {
		if bytes.Equal(x, f) {
			return i, true
		}
	}
	return -1, false
}


//function that inserts string into the cuckoo filter.
func (c *Cuckoo) insert(input string) {
	first_bucket, second_bucket, fprint := c.hashes(input)
	// first try bucket one
	b1 := c.buckets[first_bucket%c.m]
	if i, err := b1.nextIndex(); err == nil {
		b1[i] = fprint
		return
	}
	b2 := c.buckets[second_bucket%c.m]
	if i, err := b2.nextIndex(); err == nil {
		b2[i] = fprint
		return
	}
	// else we need to start relocating items
	i := first_bucket
	for r := 0; r < retries; r++ {
		index := i % c.m
		entryIndex := rand.Intn(int(c.bucket_entries))
		// swap
		fprint, c.buckets[index][entryIndex] = c.buckets[index][entryIndex], fprint
		i = i ^ uint(binary.BigEndian.Uint32(hash(fprint)))
		b := c.buckets[i%c.m]
		if idx, err := b.nextIndex(); err == nil {
			b[idx] = fprint
			return
		}
	}
	panic("cuckoo filter full")
}


// lookup needle in the cuckoo filter
func (c *Cuckoo) lookup(needle string) bool {
	first_bucket, second_bucket, fprint := c.hashes(needle)
	_, b1 := c.buckets[first_bucket%c.m].contains(fprint)
	_, b2 := c.buckets[second_bucket%c.m].contains(fprint)
	return b1 || b2
}


// delete the value from the cuckoo filter
func (c *Cuckoo) delete(needle string) {
	first_bucket, second_bucket, fprint := c.hashes(needle)
	// try to remove from f1
	b1 := c.buckets[first_bucket%c.m]
	if ind, ok := b1.contains(fprint); ok {
		b1[ind] = nil
		return
	}
   

	b2 := c.buckets[second_bucket%c.m]
	if ind, ok := b2.contains(fprint); ok {
		b2[ind] = nil
		return
	}
}


func main() {
	c := NewCuckoo(10, 0.1)
	c.insert("hello")
	c.insert("world")
	ok := c.lookup("world")
	fmt.Printf("%v\n", ok)
	c.delete("world")
	ok = c.lookup("world")
	fmt.Printf("%v\n", ok)
}

Time & Space complexity of Cuckoo Filter

Time complexity.

The time complexity of delete is O(1) because it does not depend upon the input size.
The time complexity of lookup is also O(1) because it does not depend upon the input size.
The time complexity of insertion has a reasonably high probability of O(1) if the load is well managed.

Space complexity.

A cuckoo filter requires ( log₂ (1/ϵ) + 2 ) / α bits of space per inserted key

Note:

α is the hash table load factor.The load factor is the average number of key-value pairs per bucket.It is calculated using formula load factor = total number of key-value pairs / number of buckets.
ϵ is the false positive rate.

Example: If the false positive rate is 3% and the load factor is around 95.5% then ϵ is .03 and α is 0.955
substituting these values in the formula
bits of space per inserted key =( log₂ (1/0.03) + 2 ) / 0.955
( log₂(33.333) + 2 ) / 0.955
( 5.059 + 2 ) / 0.955
7.059 / 0.955
7.391.
So it takes approximately 7 bits per inserted key.

Advantages of Cuckoo filter over Bloom filter

It takes less time for lookups.
The cuckoo filter has fewer false positives than the bloom filter for the same number of items stored.
It supports the deletion of items.
It is simple to implement than counting bloom filters.

Limitation of Cuckoo filter

It can only delete elements that are known to be inserted before.
Insertion can fail and rehashing is required like other cuckoo hash tables.

With this article at OpenGenus, you must have the complete idea of Cuckoo Filter. Enjoy. Read more:

Bloom Filter: Better than Hash Map by Harsh Bardhan Mishra
Book on Probabilistic Data Structures by Aditya Chatterjee and Ethan Z. Booker

Cuckoo filter [Explained]

Data Structures probabilistic algorithm Culture