We shall be discussing Delta rule in neural networks that is used to updated weights during training a Neural Network.

Table of Contents:

1. Introduction
2. Mathematical Definition
3. Application
4. Derivation of delta rule

Introduction

The delta rule is a formula for updating the weights of a neural network during training. It is considered a special case of the backpropagation algorithm. The delta rule is in fact a gradient descent learning rule.
Recall that the process of training a neural network involves iterating over the following steps:

• A set of input and output sample pairs are selected randomly and run through the neural network. The network makes predictions on these samples.
• The loss between the predictions and the true values is computed.
• Adjust the weights in a direction that makes the loss smaller.

The delta rule is one algorithm that can be used repeatedly during training to modify the network weights to reduce loss error.

Mathematical Definition

For the \(j\)th neuron of a neural network with activation function \(g(x)\), the delta rule for updating the neuron's \(i\)th weight, \(w_{ji}\) is given by:
$$ \Delta w_{ji}=\alpha (t_{j}-y_{j})g'(h_{j})x_{i} $$
where
\(\alpha\) is the learning rate,
\(g'\) is the derivative of the activation function \(g\),
\(t_{j}\) is the target output,
\(h_{j}\) is the weighted sum of the neuron's inputs obtained as \(\sum x_{i}w_{ji}\),
\(y_{j}\) is the predicted output,
\(x_{i}\) is the \(i\)th input.

For a neuron with a linear activation function, the derivative of the activation function is constant and so the delta rule in this case can be simplified as:
$$ \Delta w_{ji}=\alpha (t_{j}-y_{j})x_{i} $$

Application

The generalized delta rule is important in creating useful networks capable of learning complex relations between inputs and outputs. Compared to other early learning rules like the Hebbian learning rule or the Correlation learning rule, the delta rule has the advantage that it is mathematically derived and directly applicable to Supervised Learning. In addition, unlike the Perceptron learning rule which relies on the use of the Heaviside step function as the activation function which means that the derivative does not exist at zero, and is equal to zero elsewhere, the delta rule is applicable to differentiable activation functions like \(\tanh\) and the sigmoid function.
Let us consider a concrete application of the delta rule to the training step of a neural network. For this example, we define the characteristics of the neural network (see image below).

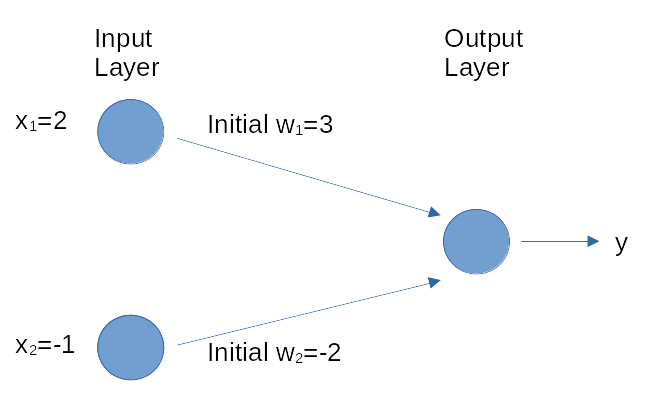
We assume the task is a binary classification problem involving two features and that the neural network uses the rectified linear (ReLU) unit as activation function and has zero bias. In addition, the learning rate is \(0.01\) and the current weight (which is a vector) is \((3,-2)\) while the next training batch consists of just one input-output pair of \(x = (2, -1)\) and the target output \(y = 0\). Running the neural network on sample \(x\) gives a predicted output \(y = 1\). The network weights will be updated as follows:
Mathematically, ReLU is defined as \(g(x) = max(x, 0)\) and its derivative
$$ \begin{equation}
g'(x)=
\begin{cases}
1 & \text{if } x \gt 0,\\
0 & \text{otherwise }
\end{cases}
\end{equation} $$

$$ \Delta w_{ij} = 0.01 * (0-1) * (1, 0).(2,-1) = (-0.02, 0) $$
New weights = \((3, -2) - (-0.02, 0) = (2.98, -2) \).

Derivation of the Delta Rule

This treatment follows the derivation of the delta rule on Wikipedia. The delta rule is derived by attempting to minimize the error in the output of the neural network through gradient descent. The error in a neural network's outputs can be measured as:
$$ E = \sum_{j}{\frac {1}{2}}(t_{j}-y_{j})^{2} $$

In this case, we wish to move through "weight space" of the neuron (the space of all possible values of all of the neuron's weights) in proportion to the gradient of the error function with respect to each weight. In order to do that, we calculate the partial derivative of the error with respect to each weight. For the \(i\)th weight, this derivative can be written as

$$ \frac {\partial E}{\partial w_{ji}} $$

Because we are only concerning ourselves with the \(j\)th neuron, we can substitute the error formula above while omitting the summation:

$$ {\frac {\partial E}{\partial w_{ji}}}={\frac {\partial \left({\frac {1}{2}}\left(t_{j}-y_{j}\right)^{2}\right)}{\partial w_{ji}}} $$
Next we use the chain rule to split this into two derivatives:

$$ {\frac {\partial \left({\frac {1}{2}}\left(t_{j}-y_{j}\right)^{2}\right)}{\partial y_{j}}}{\frac {\partial y_{j}}{\partial w_{ji}}} $$
To find the left derivative, we simply apply the chain rule:

$$ =-\left(t_{j}-y_{j}\right){\frac {\partial y_{j}}{\partial w_{ji}}} $$

To find the right derivative, we again apply the chain rule, this time differentiating with respect to the total input to \(j\), \(h_{j}\):

$$ =-\left(t_{j}-y_{j}\right){\frac {\partial y_{j}}{\partial h_{j}}}{\frac {\partial h_{j}}{\partial w_{ji}}} $$

Note that the output of the \(j\)th neuron, \(y_{j}\), is just the neuron's activation function \(g\) applied to the neuron's input \(h_{j}\). We can therefore write the derivative of \(y_{j}\) with respect to \(h_{j}\) simply as \(g\)'s first derivative:

$$ =-\left(t_{j}-y_{j}\right)g'(h_{j}){\frac {\partial h_{j}}{\partial w_{ji}}} $$
Next we rewrite \(h_{j}\) in the last term as the sum over all \(k\) weights of each weight \(w_{jk}\) times its corresponding input \(x_{k}\):

$$ =-\left(t_{j}-y_{j}\right)g'(h_{j}){\frac {\partial \left(\sum_{i}x_{i}w_{ji}\right)}{\partial w_{ji}}} $$

Because we are only concerned with the \(i\)th weight, the only term of the summation that is relevant is \(x_{i}w_{ji}\). Clearly,

$$ \frac {\partial x_{i}w_{ji}}{\partial w_{ji}}=x_{i}, $$
giving us our final equation for the gradient:

$$ \frac {\partial E}{\partial w_{ji}}=-\left(t_{j}-y_{j}\right)g'(h_{j})x_{i} $$
As noted above, gradient descent tells us that our change for each weight should be proportional to the gradient. Choosing a proportionality constant \(\alpha\) and eliminating the minus sign to enable us to move the weight in the negative direction of the gradient to minimize error, we arrive at our target equation:

$$ \Delta w_{ji}=\alpha (t_{j}-y_{j})g'(h_{j})x_{i}. $$