
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we have explored the algorithm on how to find the diameter of the tree using height of each node. This will take linear time O(V+E) time complexity.
What is Diameter of a tree ?
Diameter of tree is defined as the no. of nodes in the longest path between leaf nodes nodes of a tree ( undirected graph ) , it is also called the width of the tree.
How to find diameter of the tree ?
Well , there are two more methods apart from the methods mentioned in this article to find the diameter of the tree , so if your are interested then you can look at this article:
In this article we will be discussing the method to find the diameter of the tree using height of each node -
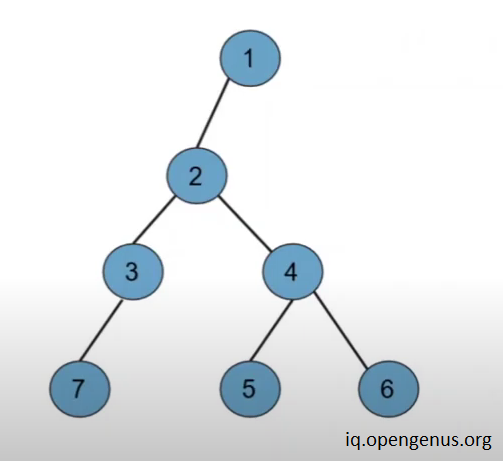
Explanation
1.we can consider various example like the one shown in the above image and we can say that there is only one node in the whole tree from which sum of height of left subtree and right subtree is maximum apart from this node all the nodes have either same or smaller heights of left and right subtree.
- we can also find the height of left subtree and right subtree from every node using very simple recursive function.
3.all we need to do is find that single node from which sum of height of left subree and right subtree is maximum and just update the ans.
4.so , we will just traverse the whole tree find the height of left subtree and right subtree from every node and update our answer if we find any greater diameter.
5.After traversing the whole tree we will be having the diameter of the tree.
Algorithm
As we will be using the recursive function so first let's define the base case
- In the recursive function if the current node is null then it will not contribute to diameter of the tree therefore we will return 0.
2.If the current node is not null then we will find the height of left and right subtree recursively .
3.Now , we will just add 1 for the current node to height of left and the right subtree and just update the ans if it's is greatest diameter we have found.
- It might also be possible that current node is not that node from which sum of heights of left and right subtree is maximum so we will return 1 ( for the current node ) + max( height of left subtree , height of right subtree ) .
5.we will keep repeating the steps 1 , 2 , 3 and 4 until whole tree is traversed and at the end after travsersing the whole tree we will have the diameter of the tree in the ans variable.
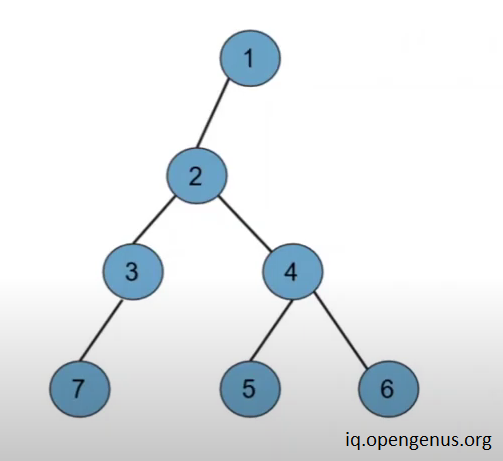
Code
#include<iostream>
using namespace std ;
// make a class for nodes of the tree
class node{
public :
node *left ;
node *right ;
node(){
left = nullptr ;
right = nullptr ;
val = 0 ;
}
} ;
// let's declare the ans of the problem as global variable so
// we don't need to the pass the value of variable in
// every function call
int ans = 0 ;
// this is the recursive function to find the diameter of the tree
int diameter( node *root ){
// if the current node is null means it won't count in the diameter of the tree therefore returning 0
if( root == nullptr ) return 0 ;
// finding the height of the tree from the left node of the current node
int left = diameter( root->left ) ;
// finding the height of the tree from the right node of the current node
int right = diameter( root->right ) ;
// current node might be the node from which diameter passes
// therefore updating the ans for every node
ans = max( ans , left + right + 1 ) ;
// here we are returning the max of left and right of the current node as only one of them will
// contribute to diameter as we are returning this value for the upper node and we are adding
// 1 for the current node
return max( left , right ) + 1 ;
}
int main(){
// the tree created in the below code is the one shown in the image
node *root = new node ;
root->left = new node ;
root->left->left = new node ;
root->left->left->left = new node ;
root->left->right = new node ;
root->left->right->left = new node ;
root->left->right->right = new node ;
// now let us call the recursive diameter function to find the diameter of the tree
diameter( root ) ;
// now let's print the diameter of the tree
cout<<ans<<" is the diameter of the tree \n" ;
return 0 ;
}
Output
5 is the diameter of the tree
Time and Space
time and space complexity of the algorithm shown in the above article is O(V+E)
as we require O(V+E) time to traverse the whole tree and we are using recursion therefore stack will be created which will of the order of O(V) in the worst case
therefore time and space complexity of the algorithm is:
