Diameter of N-ary tree using Dynamic Programming

In this problem, we are given input as the reference to the root of an N-ary tree.
We need to calculate the diameter of the tree that is the longest path between any two nodes using Dynamic Programming.

A tree is an extensively used data structure in the world of programming. Every node in a tree can have more further subdivisions. The bottom-most nodes of a tree that have no sub-divisions, are called the leaf nodes.

We know that in a binary tree, each node has no more than 2 children. Similarly, in an N-ary tree, each node has no more than N children. N can be any integer here.

DIAMETER OF A TREE: It is defined as the number of nodes on the longest path between 2 nodes.This path may or may not pass through the root of the tree.This path includes two leaf nodes. It is also known as the width of a tree.

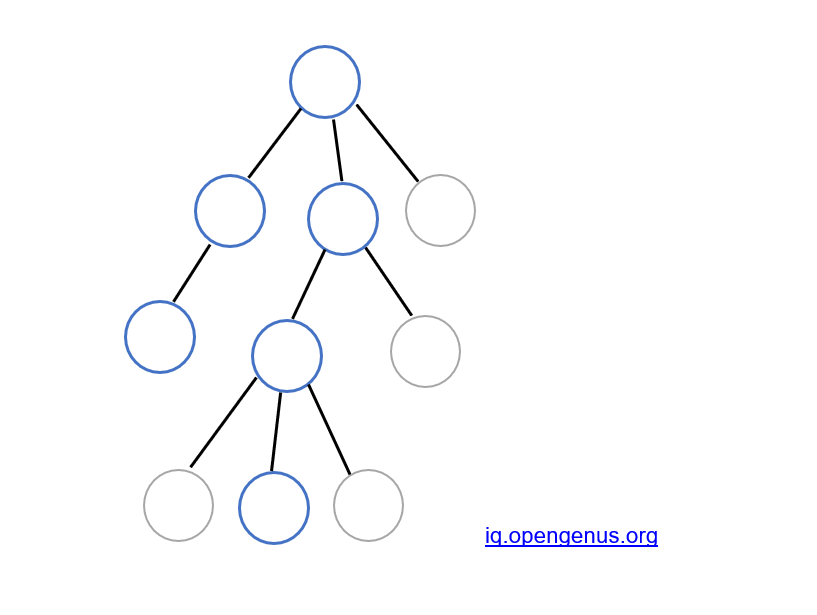
Example 1: diameter passing through the root node:

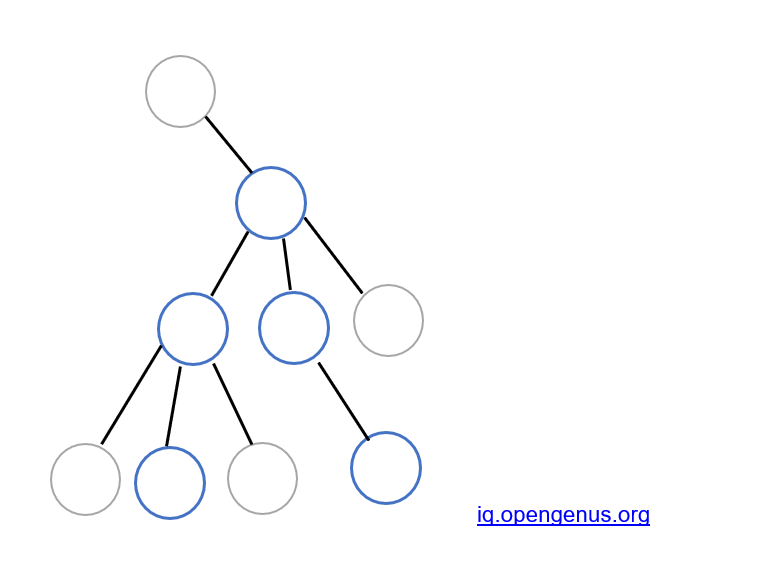
Example 2: diameter doesn't pass through the root node:

To solve this, we need to proceed by breaking it down into sub-problems that follow a similar structure and storing the values for future use. This is the approach used for Dynamic Programming.

We will be using DFS i.e Depth First Search algorithm to solve this problem. This algorithm starts at the root node of the tree and explores as far as possible along each branch before backtracking. Therefore, we start with the leaf nodes and make our way to the top.

There are 4 main variables used in this implementation:

1. FirstMax: This variable stores the height of the largest subtree of any node.

2. SecondMax: This variable stores the height of the second largest subtree of any node.

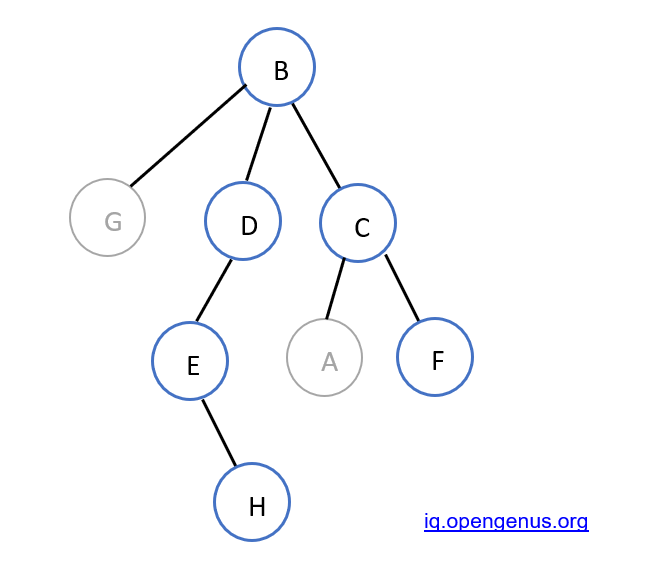
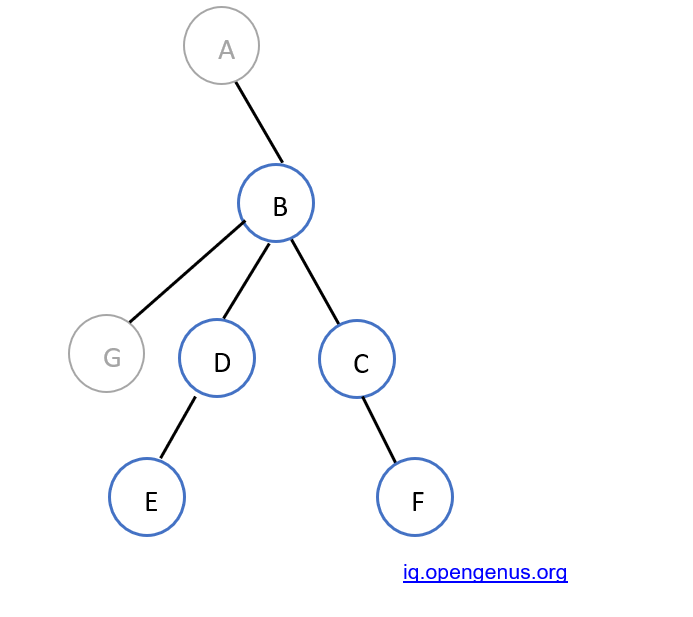
In this example, for node B, the largest subtree is D->E->H. Therefore, FirstMax = 3
The second largest subtree is C->F (or C->A). Therefore, SecondMax = 2.

For any node, by default, FirstMax and SecondMax are -1. When we discover the subtrees of the nodes through DFS, FirstMax and SecondMax are changed accordingly.

3. dp1[node] : This calculates the no. of nodes that will be in the diameter of the tree, if we consider, that for any node, the diameter doesn't pass through 2 of its subtrees.

In the given example,
the diameter passes through B->A->C->D. For node C, the diameter doesn't pass through 2 of its subtrees.It only passes through one subtree i.e. D. Hence, till node C, 2 nodes(C and D) will be in the diameter of the tree. dp1[C] = 2

dp1[node] = 1 + FirstMax

4. dp2[node]: This calculates the no. of nodes that will be in diameter of the tree, if for any node, the diameter passes through two of its subtrees.

In this example,
the diameter passes through E->D->B->C->F.
For node B, the diameter passes through 2 of its subtrees. Therefore, 5 nodes are in the diameter.
dp2[B] = 5

dp2[node] = 1 + FirstMax + SecondMax

For a leaf node, we consider dp1[node]=1 and dp2[node] = 0.

There is also an extra variable max_diam, that keeps a track of the maximum diameter till that point, so as to attain the final diameter of the tree.

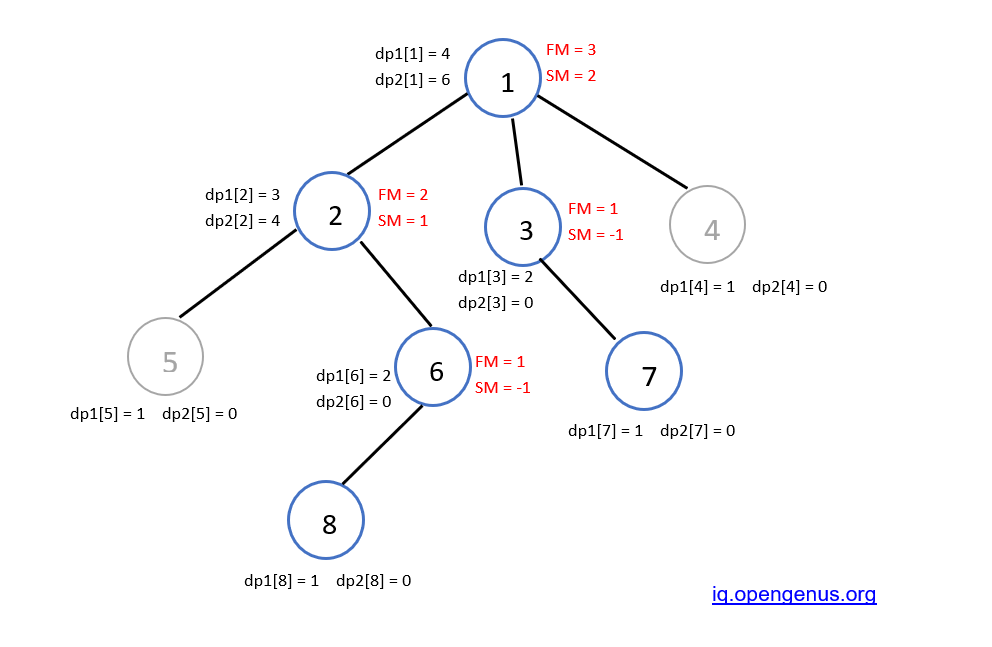
Let us walk through this problem with a basic example:

We traverse through the whole tree using DFS by starting at the leaf nodes and making our way to the top. The Firstmax, SecondMax, dp1[node] and dp2[node] are calculated along the way.

Here max_diam will be 6, which will be returned to the main function.
Therefore, the diameter of the given tree is 6.

Below is the implementation of the above approach in C++:

#include <bits/stdc++.h> 
using namespace std; 
  
int diameter = -1; 
int max_diam = 0;
  
// Function to find the diameter of the tree 
// using Dynamic Programming 
int dfs(int node, int parent, int dp1[], int dp2[], list<int>* adj) 
{ 
  
    // Store the first maximum and secondmax 
    int firstmax = -1; 
    int secondmax = -1; 


    // cout<<"\nmax_diam is "<<max_diam;

  
    // Traverse for all children of node 
    for (auto i = adj[node].begin(); i != adj[node].end(); ++i) { 

        if (*i == parent) 
            continue; 

        // cout<<"\nbefore dfs node is "<<node;

        // Call DFS function again 
        dfs(*i, node, dp1, dp2, adj); 

        // cout<<"\nafter dfs node is "<<node;
  
        // Find first max 
        if (firstmax == -1) { 
            firstmax = dp1[*i]; 
        } 
        else if (dp1[*i] >= firstmax) // Secondmaximum 
        { 
            secondmax = firstmax; 
            firstmax = dp1[*i]; 
        } 
        else if (dp1[*i] > secondmax) // Find secondmaximum 
        { 
            secondmax = dp1[*i]; 
        } 
    } 
  
    // Base case for every node 
    dp1[node] = 1; 
    if (firstmax != -1) // Add 
        dp1[node] += firstmax; 
  
    // Find dp[2] 
    if (secondmax != -1) 
        dp2[node] = 1 + firstmax + secondmax; 
  
    
    // Return maximum of both 
    if (max(dp1[node], dp2[node])>max_diam)
        max_diam = max(dp1[node], dp2[node]);


    return max_diam; 
} 
  
// Driver Code 
int main() 
{ 
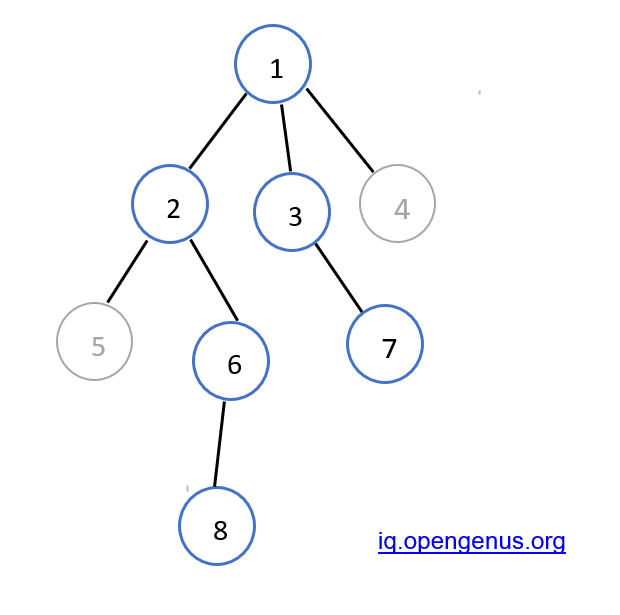
    int n = 8; 
  
    /* Constructed tree is  
          1  
        / \ \ 
        2  3 4 
       / \  \ 
       5  6  7
          /
          8

    */
    list<int>* adj = new list<int>[n + 1]; 
  
    /*create undirected edges */
    adj[1].push_back(2); 
    adj[2].push_back(1); 
    adj[1].push_back(3); 
    adj[3].push_back(1);
    adj[1].push_back(4); 
    adj[4].push_back(1);  
    adj[2].push_back(5); 
    adj[5].push_back(2); 
    adj[2].push_back(6); 
    adj[6].push_back(2); 
    adj[3].push_back(7); 
    adj[7].push_back(3); 
    adj[6].push_back(8); 
    adj[8].push_back(6); 
    
  
    int dp1[n + 1], dp2[n + 1]; 
    memset(dp1, 0, sizeof dp1); 
    memset(dp2, 0, sizeof dp2); 

  
    // Find diameter by calling function 
     cout << "Diameter of the given tree is "
          << dfs(1, 1, dp1, dp2, adj) << endl; 
  
    return 0; 
}

Output:

Diameter of the given tree is 6

Time complexity: O(n)

Conclusion:

We have studied one of the many approaches for calculating the diameter of an N-ary tree using Dynamic Programming.