
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
The day will come when you will apply for the job that you have dreamt of for years, you apply for it and got a call from HR for an interview. Although this article may help you as a recap, you will need a deep understanding of the Sorting algorithms to crack any technical interview. Here we are, to help you chase your dreams!
Not only for the sake of interview preparation, as an enthusiastic programmer it's good to know algorithms.
Let's start learning then!
We have covered:
- Shell Sort
- Heap Sort
- Bucket Sort
- Radix Sort
- Counting Sort
1.Shell Sort
Shell sort is basically a segmented insertion sort that divides a collection, say array into several smaller non-contiguous segments. The distance between consecutive elements in one segment is called a gap. Each segment is sorted within itself using an insertion sort. Then divide it into larger segments (smaller gaps) and repeat sort. Continue until single segment (gap = 1) - I.e array is completely sorted.
Algorithm
Step 1 − Initialize the value of h.
Step 2 − Divide the collection,say list into a smaller sub-list of equal interval h.
Step 3 − Sort these obtained small sub-lists using insertion sort.
Step 3 − Repeat the above process until the complete list is sorted.
Let's understand shell sort with an example:
Consider an array a[4]={89,12,54,34,48}
Initially 89 12 54 34 48
Start with gap=n/2 , gap = 2 in this case
1st iteration : 89 12 54 34 48 SWAP
2nd iteration : 54 12 89 34 48 NO SWAP
3rd iteration : 54 12 89 34 48 SWAP
54 12 48 34 89 SWAP
After first pass : 48 12 54 34 89
Reduce the gap now. Gap=n/4 , gap = 1 in this case
1st iteration : 48 12 54 34 89 SWAP
2nd iteration : 12 48 54 34 89 SWAP
3rd iteration : 12 48 54 34 89 SWAP
12 48 34 54 89 SWAP
4th iteration : 12 34 48 54 89, which is completely a sorted array.
Quick Analysis
- Time complexity for worst case - O(n^2)
- Worst-case space complexity - О(n) total, O(1) auxiliary
2.Heap Sort
Heapsort is an interesting algorithm that uses heaps for sorting the given set of elements. Construction of heap and the array representation of heap is an important area to look into before understanding the algorithm.
Algorithm
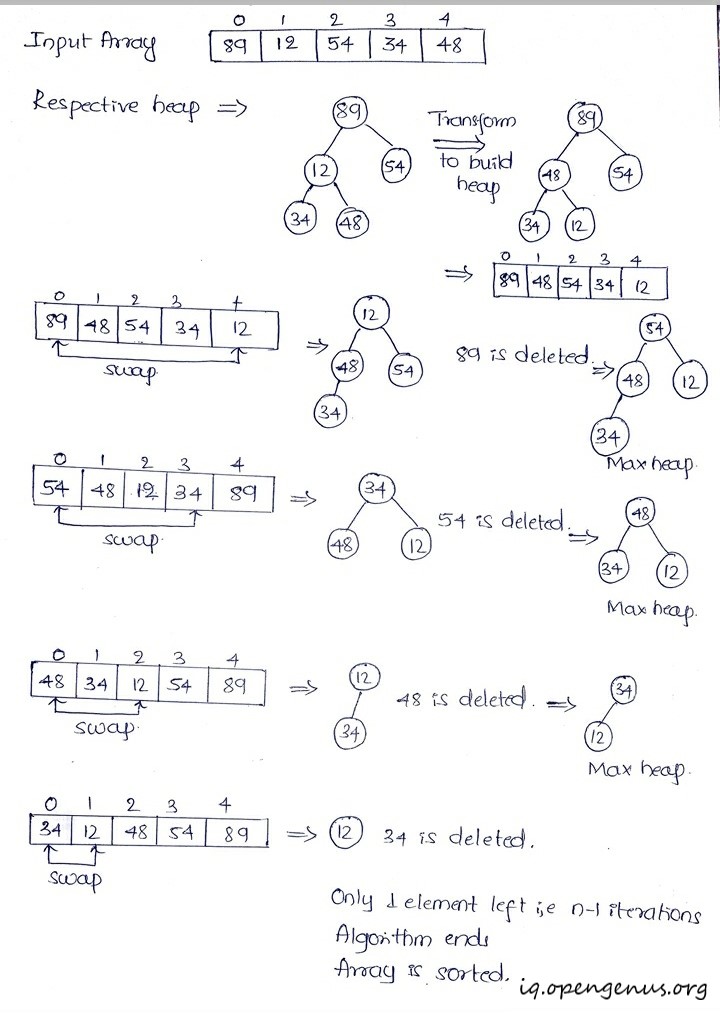
Stage 1: Construct a heap for a given element of the array.
Step 2: Create maxheap(Ascending) for the heap we just constructed.
Stage 3 (maximum deletions): Apply the root-deletion(swap the root node with the last node in the array and delete the last node from the heap) operation (n−1) times
to the remaining heap.Where n is the no. of the element in the array
Let's understand heapsort with an example:
Quick Analysis
- Best, average, and worst-case time complexity: nlogn. This is independent of the distribution of data.
- Worst-case space complexity- O(n) total O(1) auxiliary.
When to use heap sort?
- When you don't need a stable sort.
- When worst-case performance is of higher importance than average-case performance. It's guaranteed to be O(N log N), and uses O(1) auxiliary space, meaning that you won't unexpectedly run out of heap or stack space on worst-case or very large inputs.
Non-comparison based sorting
In non-comparison based sorting, elements of array are not compared with each other to find the sorted array.
3.Bucket Sort
Bucket sort is a non-comparison based sorting algorithm that works by distributing the elements of an array into a number of buckets. The bucket is nothing but a kind of container which holds elements. Each bucket or a container is then sorted individually, either using a different sorting algorithm or by recursively applying the bucket sorting algorithm.
Algorithm
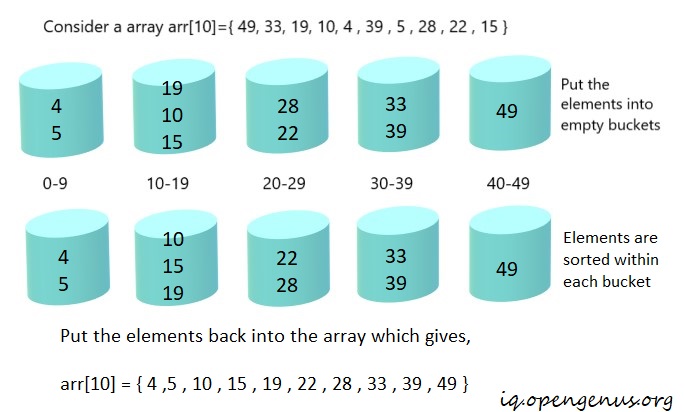
Step 1: Set up an array of initially empty "buckets".
Step 2: Scatter- Go over the original array, putting each object in its bucket.
Step 3: Sort each non-empty bucket.
Step 4: Gather- Visit the buckets in order and put all elements back into the original array.
Let's understand heapsort with an example:
Quick Analysis
- Best and average time complexity: n+k where k is the number of buckets and n is the number of elements in the array.
- Worst case time complexity: n^2 if all elements belong to the same bucket.
- Worst-case space complexity: O(n.k)
When to use bucket sort?
- Use bucket sort when you can guarantee that your input is approximately uniformly distributed. In this case, bucket sort works really well.
4.Radix Sort
Radix sort is a non-comparision based sorting algorithm used to to sort numbers only. The algorithm sorts data with integer keys by grouping the keys by individual digits that share the same significant position and value place.
Algorithm
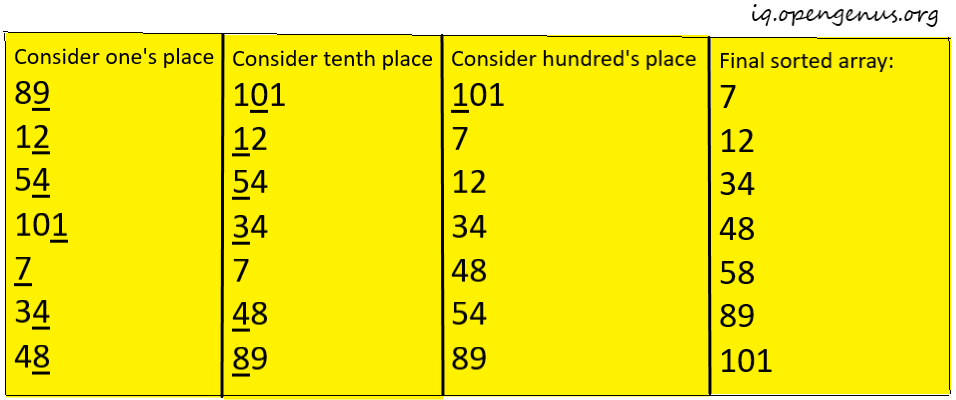
The algorithm performs the operation on every digit. So i vary from least significant to the most significant digit. For example, consider 201, i varies from 1 to 2.
Step 1: Sort input array using any stable sort say counting sort, according to the i’th digit.
Repeat step 1 until all the digits of all the array elements are sorted.
Let's undertsand radix sort with an example:
Quick Analysis
- Best, average and worst-case time complexity: nk where k is the maximum number of digits in elements of the array.
- Worst-case space complexity: O(w+n)
When to use Radix sort?
- When log(N) is significantly larger than K, where K is the number of radix digits.
5.Counting Sort
If you wanna play with integers then this sorting technique is for you! It is based on distinct numbers between a specific range. If know hashing you can think of this process as similar to that. The algorithm counts the number of distinct objects. Then we do an arithmetic operation like taking the average to calculate the position of each object in the output sequence.
Algorithm
Step 1: Take an empty array that stores the no. of occurrences of each element. Let's call the array count_array.
The indexes of the count array are in the range from 0 to max. of input_array.
Step 2: Add the current value and the previous one until the end of the count_array, thereby performing the arithmetic operation
Step 3: Find the values of the input_array elements w.r.t count_array.
Step 4: Reduce the value at the count_array while constructing a sorted array.
Let's understand counting sort with an example:

Quick Analysis
- Best, average, and worst-case time complexity: o(n+k) where k is the size of count array(i.erange of the non-negative key values)
- Worst-case space complexity- O(n+k)
When to use count sort?
- When you are sorting integers with a limited range.
Let's summarise the time complexity and space complexity of each algorithms.

Hope you enjoyed working with algorithms.
Keep practicing and wish you the best!
