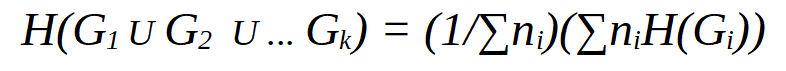Entropy of Graph

Reading time: 10 minutes

In physical sciences, entropy is a measure of disorder of a system. Similarly in graph theory entropy is the index for describing the structure and function of a network. Entropy is related to amount of information stored in a graph. This is used in field of computer science to check compression of data as compressed data is more random and hence has higher entropy.

The entropy of a graph is an information theoretic functional which is defined on a graph with a probability density on its vertex set.

This functional was orignally proposed by J. Korner in 1973 to tudy minimum number of codewords required to represent an information source.

One of the most important properties of entropy of a graph is that it is subadditive with repect to union of graphs. This leads to its application in graph covering problem as well as problem of perfect hashing.

There are various ways for calculating entropy of a graph for undirected and directed graphs we will now have a look at these and their usage in more detail.

Entropy of a graph

Graph entropy has its roots set in information theory and one of the first estimation was given by Shanon it described in general the minimum number of bits required to encode a particular probablity distribution. If an outcome has probablity of pi
then number of bits required to encode the outcome are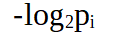

and the number of bits required are bits required of each outcome times the probablity of that event occuring that comes out to be

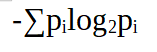
which is also the Shanon entropy. When applying this on graphs the events are usually presumed to be the nodes of the graph. This was cited by J. Korner in his 1973 paper that talked about graph entropy.

Let G = (V,E) be an undirected graph. The graph entropy og G, denoted as H(G) is defined as

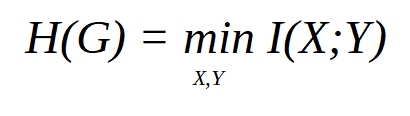
Whrere X is chosen uniformly from V,Y ranges over independent sets of G, the joint distribution of X and Y is such that X ∈ Y with probablity one, and I is the mutual information of X and Y.

Basic Properties of Graph Entropy

The major properties of graph entropy are monotonicity, sub-additivity and additivity over vertex substitution

1. Monotonicity
   • Let F be a spanning subgraph of a graph G. Then for any probablity density P we have H(F,P) <= H(G,P)
   • A subgraph always has entropy less than or equal to the supergraph.
   • For graphs F and G mentioned, we have VP(G) ⊆ VP(F). This immidiately implies the stetement above.
2. **Sub-Additivity
   • Given two graphs G₁ = (V,E₁) and G₂ = (V,E₂) on the same vertex set set V. The graph union G₁U G₂ = (V,E₁ U E₂) satisfies H(G₁ U G₂) <= H(G₁) + H(G₂)
   • The entropy of union of two graphs is less than or equal to the sum of entropy of graphs individually.
3. Arithmetic mean of disjoint unions of graphs G₁, G₂..., G_k on set of disjoint vertices with n₁, n₂..., n_k vertices respectively Then.
   • 

Entropy of some special graphs

• A graph with no edges have entropy 0.
• A complete graph with n vertices have entropy log₂n.
• A complete balanced k-partite graph has entroop log₂k.
• From above we can see complete bipartite graphs have entropy 1.
• Complete bipartite graphs with n vertices in one partition and m in another partition have entropy H(n/m + n). Where H is the binary entropy function.

Entropy of Directed Graphs

Entropy is an important aspect when looking at a network but primarily all of the studies done earlier have been centered around undirected graphs and the stidy of directed graphs are a more recent advancement.
Compared to an undirected graphs directed graphs involve special asymmetric transfer.

However for directed graphs we use Chung's generalisation or von Neuman approach which is based on graph laplacian , this can be applied to both weakly and strongly directed graphs a simple form of this be represented in simple node in-degree out-degree based statistics.

This research on directed networks are significant to quantify structural information of the whole network. To quantify the entropy of a directed graph we rely on degreee based algorithms which measure the importance of vertices and is usually more sensitive than other indicators.

Now we have shifted to eigenvalue based entropy calculations which depend upon adjacency matrix. From typical modelsof complex networks a model of directed network is proposed that considers in-direction of node connections and eigenvalue based etropy of three matrices are calculated for directed nearest neighbour coupling. Directed small-world, directed scale-free and directed random networks.

Comparison

Compared to a directed network an undirected network has higher entropy for lower number of edges and this trend changes as number of edges increases. Entropy is mainly dependent on number of edges and directed networks are again a special case due to the asymmetric transfer.

Example

Now we will see how we calculte entropy of graphs using the above knowledge

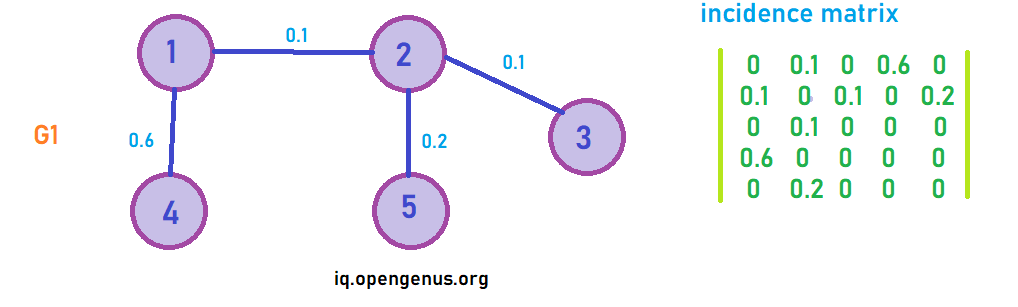
In the above graph we calculate the entropy as follows
Using the incidence matrix and using the shanon entropy formula from above

Entropy = -[0.6 x log₂(0.6) + 0.2 x log₂(0.2) + 0.1 x log₂(0.1) + 0.1 x log₂(0.1)] = 1.5710

Now we have another similar graph

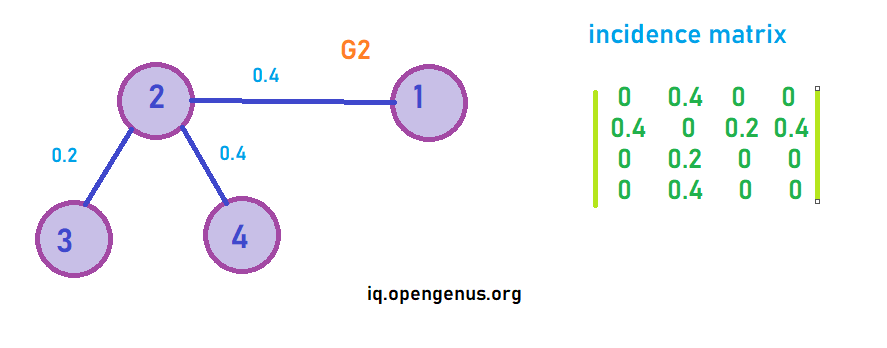
Similar to what we did above

Entropy = -[0.4 x log₂(0.4) + 0.4 x log₂(0.4) + 0.2 x log₂(0.2) ] = 1.5230

Using these two graphs we have noted how entropy is calculated for graphs

Execution

Now we will try to implement the entropy of simple undirected graph by help of a simple C++ code

Pseudocode

• Take the incidence matrix of the as input and store it in a 2D vector
• Traverse the upper triangular matrix so as to consider each edge only once and for each non zero value increment to the sum variable the output of function p*log₂p
• The sum will always be zero and the magnitude of this sum will be the entropy
• Output the entropy to the user

Code

#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

int main(){
    int n;
    cout << "Enter number of vertices" << endl;
    cin >> n;
    // we take a 2D vector to store the incidence matrix of the graph
    vector<vector<float>> mat( n , vector<float> (n, 0));
    cout << "Enter the incidence matrix of the graph : " << endl;
    for(int i = 0 ; i < n ; i++){
        for(int j = 0; j < n; j++) {
            float x;
            cin >> x;
            mat[i][j] = x;
        }
    }
    // sum stores the sum for shanon entropy
    float sum = 0.0;
    for(int i = 0 ; i < n ; i++){
        for(int j = i; j < n; j++) {
            if(mat[i][j] != 0){
                sum += mat[i][j]*log2(mat[i][j]);
            }
        }
    }
    cout << "The entropy of the graph is : " << endl;
    cout << -sum << endl;
}

Now lets try to find entropy of graph G2 by implementing the above code

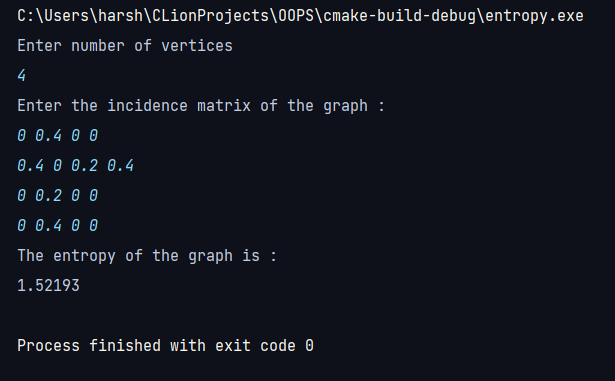
and we see the output of the program is within margin of error of what we had calculated above.