Freivalds’ algorithm for verifying Matrix Multiplication

Freivalds' algorithm is a probabilistic randomized algorithm used to verify matrix multiplication. Given three n x n matrices, Freivalds' algorithm determines in O(kn^2) whether the matrices are equal for a chosen k value with a probability of failure less than 2^-k.

Freivalds' algorithm

1. Input: n×n matrices A, B and C.

2. We would like to verify if A×B=C.
   Choose a n×1 column vector r→∈{0,1}n, uniformly and at random. In other words, each component of the vector is either 0 or 1 and chosen randomly and uniformly.

3. Compute A⋅(B⋅r) and C⋅r. This takes Θ(n^2) time.

4. Now comes the output

   • If A⋅(B⋅r)≠C⋅r, output FALSE. In other words, we say that the given matrix multiplication is incorrect. This has a probability of correctness = 1.
   • If A⋅(B⋅r)=C⋅r, output TRUE. In other words, we say that the given matrix multiplication is correct. This has a probability of correctness ≥1/2.

Example

Let A,B,C are the matrices such that A × B = C.A random two-element vector with entries equal to 0 or 1 is selected Vector r=[1,1] .

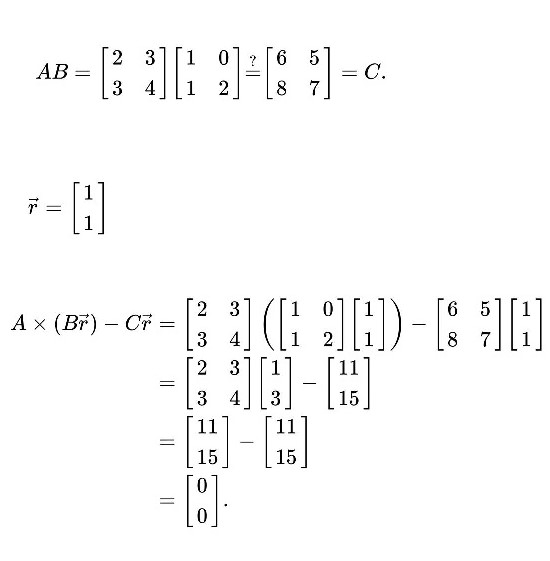
This yields the zero vector, suggesting the possibility that AB = C. However, if in a second trial the vector r=[1,0] is selected, the result becomes:

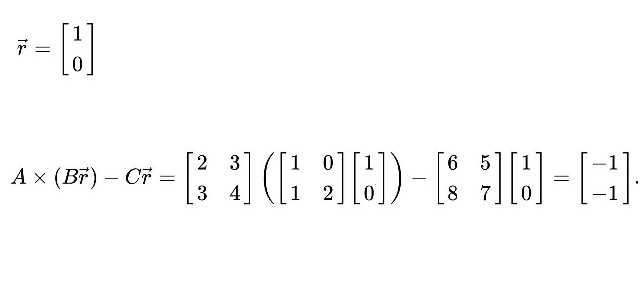
The result is nonzero, proving that in fact AB ≠ C.
There are four two-element 0/1 vectors, and half of them give the zero vector in this case Vector r=[0,0] and r=[1,1].so the chance of randomly selecting these in two trials (and falsely concluding that AB=C) is 1/22 or 1/4. In the general case, the proportion of r yielding the zero vector may be less than 1/2, and a larger number of trials would be used, rendering the probability of error very small.

Error analysis

Let p equal the probability of error. We claim that if A × B = C, then p = 0, and if A × B ≠ C, then p ≤ 1/2.

Case A × B = C:
Regardless of the value of vector r, since it uses only that A × B - C =0. Hence the probability for error in this case would be zero.

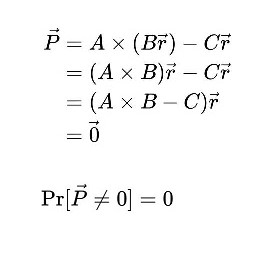
Case A × B ≠ C:

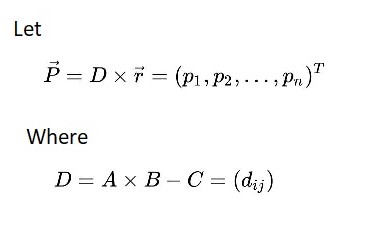
Since A × B ≠ C, we have that some element of D is nonzero. Suppose that the element d≠0.For some constant y. Using Bayes' Theorem, we can partition over y.

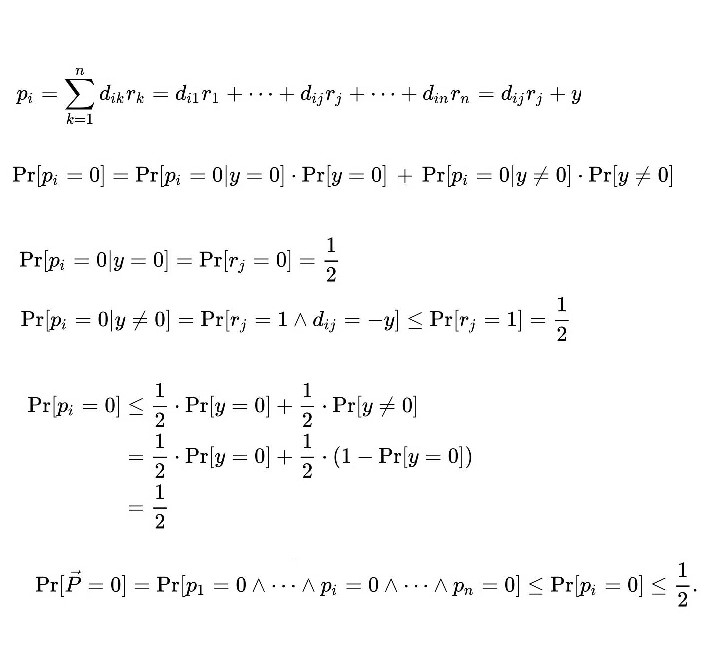
Pseudocode

• Generate an n × 1 random 0/1 vector r.
• Compute P = A × (Br) – Cr.
• Return true if P = ( 0, 0, …, 0 )T, return false otherwise.

Br = matrix B multiplied by Vector r.
Cr = matrix C multiplied by Vector r.

Complexity

• Worst case time complexity: Θ(kn^2)

• Space complexity: Θ(n^2)
  k = number of times the algorithm iterates.

Implementations

• C++

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
int main(int argc, char **argv)
{
    cout << "Enter the dimension of the matrices: " << endl;
    int n;
    cin >> n;
    cout << "Enter the 1st matrix: " << endl;
    double a[n][n];
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cin >> a[i][j];
        }
    }
    cout << "Enter the 2nd matrix: " << endl;
    double b[n][n];
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cin >> b[i][j];
        }
    }
    cout << "Enter the result matrix: " << endl;
    double c[n][n];
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cin >> c[i][j];
        }
    }
    //random generation of the r vector 
    // containing only 0/1 as its elements
    double r[n][1];
    for (int i = 0; i < n; i++)
    {
        r[i][0] = rand() % 2;
    }
    //test A * (b*r) - (C*) = 0
    double br[n][1];
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < 1; j++)
        {
            for (int k = 0; k < n; k++)
            {
                br[i][j] = br[i][j] + b[i][k] * r[k][j];
            }
        }
    }
    double cr[n][1];
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < 1; j++)
        {
            for (int k = 0; k < n; k++)
            {
                cr[i][j] = cr[i][j] + c[i][k] * r[k][j];
            }
        }
    }
    double abr[n][1];
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < 1; j++)
        {
            for (int k = 0; k < n; k++)
            {
                abr[i][j] = abr[i][j] + a[i][k] * br[k][j];
            }
        }
    }
    //    br = multiplyVector(b, r, n);
    //    cr = multiplyVector(c, r, n);
    //    abr = multiplyVector(a, br, n);
    //abr-cr
    for (int i = 0; i < n; i++)
    {
        abr[i][0] -= cr[i][0];
    }
    bool flag = true;
    for (int i = 0; i < n; i++)
    {
        if (abr[i][0] == 0)
            continue;
        else
            flag = false;
    }
    if (flag == true)
        cout << "True";
    else
        cout << "False";
}

Applications

• Fingerprinting is a well known technique, which is often used in designing Monte Carlo algorithms for verifying identities involving matrices, integers and polynomials.

• Freivalds' algorithm frequently arises in introductions to probabilistic algorithms due to its simplicity and how it illustrates the superiority of probabilistic algorithms in practice for some problems.