Strassen’s Matrix Multiplication algorithm

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Reading time: 25 minutes | Coding time: 10 minutes

Matrix Multiplication is one of the most fundamental operation in Machine Learning and optimizing it is the key to several optimizations. In general, multipling two matrices of size N X N takes N^3 operations. Since then, we have come a long way to better and clever matrix multiplication algorithms. Volker Strassen first published his algorithm in 1969. It was the first algorithm to prove that the basic O(n^3) runtime was not optiomal.

The basic idea behind Strassen's algorithm is to split A & B into 8 submatricies and then recursively compute the submatricies of C. This strategy is called Divide and Conquer.


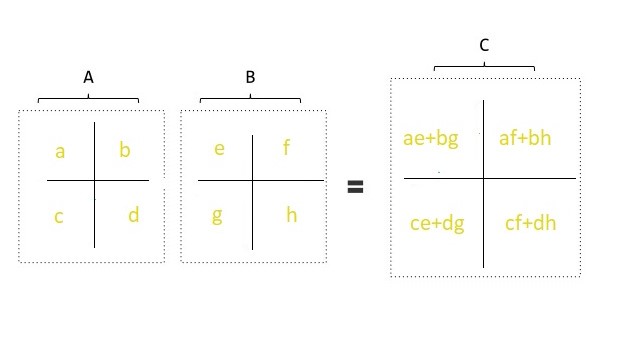
Consider the following matrices A and B:

matrix A = |a b|, matrix B = |e f|
           |c d|             |g h|

There will be 8 recursive calls:

a * e
b * g
a * f
b * h
c * e
d * g
c * f
d * h

We then use these results to compute C's submatricies.



matrix C = |ae+bg af+bh|
           |ce+dg cf+dh|

The above strategy is the basic O(N^3) strategy.

Using the Master Theorem with T(n) = 8T(n/2) + O(n^2) we still get a runtime of O(n^3).

Strassen's insight was that we don't actually need 8 recursive calls to complete this process. We can finish the call with 7 recursive calls and a little bit of addition and subtraction.

Strassen's 7 calls are as follows:


a * (f - h)
(a + b) * h
(c + d) * e
d * (g - e)
(a + d) * (e + h)
(b - d) * (g + h)
(a - c) * (e + f)

Our new matrix C's new quardents


matrix C = |p5+p4-p2+p6    p1+p2   |
           |   p3+p4    p1+p5-p3-p7|

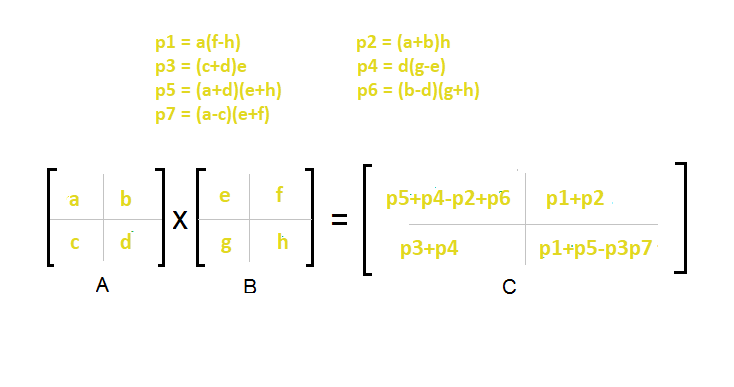
Strassen's Submatrix:


p5+p4-p2+p6 = (a+d)*(e+h) + d*(g-e) - (a+b)*h + (b-d)*(g+h)
            = (ae+de+ah+dh) + (dg-de) - (ah+bh) + (bg-dg+bh-dh)
            = ae+bg
 p1+p2 = a*(f-h) + (a+b)*h
       = (af-ah) + (ah+bh)
       = af+bh
 p3+p4 = (c+d)*e + d*(g-e)
       = (ce+de) + (dg-de)
       = ce+dg 
 p1+p5-p3-p7 = a*(f-h) + (a+d)*(e+h) - (c+d)*e - (a-c)*(e+f)
             = (af-ah) + (ae+de+ah+dh) -(ce+de) - (ae-ce+af-cf)
             = cf+dh

The time completxity using the Master Theorem.

T(n) = 7T(n/2) + O(n^2) which leads to O(n^log(7)) runtime. This comes out to approxiamtely O(n^2.8074) which is better than O(n^3)

strassen_2x2

Pseudocode

Divide matrices A and B in 4 sub-matrices of size N/2 x N/2 as shown in the above diagram.
Calculate the 7 matrix multiplications recursively.
Compute the submatricies of C.
Combine these submatricies into our new matrix C

Complexity

Worst case time complexity: Θ(n^2.8074)
Best case time complexity: Θ(1)
Space complexity: Θ(logn)

Implementations

C++


#include < iostream>
#include < vector>
#include < cmath>
#include < algorithm>
using namespace std;

int nextpowerof2(int k)
{
    return pow(2, int(ceil(log2(k))));
}
void display(vector< vector<int>> &matrix, int m, int n)
{
    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (j != 0)
            {
                cout << "\t";
            }
            cout << matrix[i][j];
        }
        cout << endl;
    }
}

void add(vector<vector<int>> &A, vector<vector<int>> &B, vector<vector<int>> &C, int size)
{
    int i, j;

    for (i = 0; i < size; i++)
    {
        for (j = 0; j < size; j++)
        {
            C[i][j] = A[i][j] + B[i][j];
        }
    }
}

void sub(vector<vector<int>> &A, vector<vector<int>> &B, vector<vector<int>> &C, int size)
{
    int i, j;

    for (i = 0; i < size; i++)
    {
        for (j = 0; j < size; j++)
        {
            C[i][j] = A[i][j] - B[i][j];
        }
    }
}

void STRASSEN_algorithmA(vector<vector<int>> &A, vector<vector<int>> &B, vector<vector<int>> &C, int size)
{
    //base case
    if (size == 1)
    {
        C[0][0] = A[0][0] * B[0][0];
        return;
    }
    else
    {
        int new_size = size / 2;
        vector<int> z(new_size);
        vector<vector<int>>
            a11(new_size, z), a12(new_size, z), a21(new_size, z), a22(new_size, z),
            b11(new_size, z), b12(new_size, z), b21(new_size, z), b22(new_size, z),
            c11(new_size, z), c12(new_size, z), c21(new_size, z), c22(new_size, z),
            p1(new_size, z), p2(new_size, z), p3(new_size, z), p4(new_size, z),
            p5(new_size, z), p6(new_size, z), p7(new_size, z),
            aResult(new_size, z), bResult(new_size, z);

int i, j;

//dividing the matrices into sub-matrices:
for (i = 0; i < new_size; i++)
        {
            for (j = 0; j < new_size; j++)
            {
                a11[i][j] = A[i][j];
                a12[i][j] = A[i][j + new_size];
                a21[i][j] = A[i + new_size][j];
                a22[i][j] = A[i + new_size][j + new_size];

                b11[i][j] = B[i][j];
                b12[i][j] = B[i][j + new_size];
                b21[i][j] = B[i + new_size][j];
                b22[i][j] = B[i + new_size][j + new_size];
            }
}

// Calculating p1 to p7:

        add(a11, a22, aResult, new_size);     // a11 + a22
        add(b11, b22, bResult, new_size);    // b11 + b22
        STRASSEN_algorithmA(aResult, bResult, p1, new_size); 
        // p1 = (a11+a22) * (b11+b22)

        add(a21, a22, aResult, new_size); // a21 + a22
        STRASSEN_algorithmA(aResult, b11, p2, new_size);
        // p2 = (a21+a22) * (b11)

        sub(b12, b22, bResult, new_size);      // b12 - b22
        STRASSEN_algorithmA(a11, bResult, p3, new_size);
        // p3 = (a11) * (b12 - b22)

        sub(b21, b11, bResult, new_size);       // b21 - b11
        STRASSEN_algorithmA(a22, bResult, p4, new_size); 
        // p4 = (a22) * (b21 - b11)

        add(a11, a12, aResult, new_size);      // a11 + a12
        STRASSEN_algorithmA(aResult, b22, p5, new_size);
        // p5 = (a11+a12) * (b22)

        sub(a21, a11, aResult, new_size);      // a21 - a11
        add(b11, b12, bResult, new_size);               
        // b11 + b12
        STRASSEN_algorithmA(aResult, bResult, p6, new_size);
        // p6 = (a21-a11) * (b11+b12)

        sub(a12, a22, aResult, new_size);      // a12 - a22
        add(b21, b22, bResult, new_size);                
        // b21 + b22
        STRASSEN_algorithmA(aResult, bResult, p7, new_size);
        // p7 = (a12-a22) * (b21+b22)

        // calculating c21, c21, c11 e c22:

        add(p3, p5, c12, new_size); // c12 = p3 + p5
        add(p2, p4, c21, new_size); // c21 = p2 + p4

        add(p1, p4, aResult, new_size);       // p1 + p4
        add(aResult, p7, bResult, new_size);  // p1 + p4 + p7
        sub(bResult, p5, c11, new_size); // c11 = p1 + p4 - p5 + p7

        add(p1, p3, aResult, new_size);       // p1 + p3
        add(aResult, p6, bResult, new_size);  // p1 + p3 + p6
        sub(bResult, p2, c22, new_size); // c22 = p1 + p3 - p2 + p6

        // Grouping the results obtained in a single matrix:
        for (i = 0; i < new_size; i++)
        {
            for (j = 0; j < new_size; j++)
            {
                C[i][j] = c11[i][j];
                C[i][j + new_size] = c12[i][j];
                C[i + new_size][j] = c21[i][j];
                C[i + new_size][j + new_size] = c22[i][j];
            }
        }
    }
}
void STRASSEN_algorithm(vector<vector<int>> &A, vector<vector<int>> &B, int m, int n, int a, int b)
{  
/* Check to see if these matrices are already square and have dimensions of a power of 2. If not,
 * the matrices must be resized and padded with zeroes to meet this criteria. */
    int k = max({m, n, a, b});

    int s = nextpowerof2(k);

    vector<int> z(s);
    vector<vector<int>> Aa(s, z), Bb(s, z), Cc(s, z);

    for (unsigned int i = 0; i < m; i++)
    {
        for (unsigned int j = 0; j < n; j++)
        {
            Aa[i][j] = A[i][j];
        }
    }
    for (unsigned int i = 0; i < a; i++)
    {
        for (unsigned int j = 0; j < b; j++)
        {
            Bb[i][j] = B[i][j];
        }
    }
    STRASSEN_algorithmA(Aa, Bb, Cc, s);
    vector<int> temp1(b);
    vector<vector<int>> C(m, temp1);
    for (unsigned int i = 0; i < m; i++)
    {
        for (unsigned int j = 0; j < b; j++)
        {
            C[i][j] = Cc[i][j];
        }
    }
    display(C, m, b);
}

bool check(int n, int a)
{
    if (n == a)
        return true;
    else
        return false;
}

int main()
{
    int m, n, a, b;
    cout << "Matrix Multiplication using Strassen algorithm" << endl;
    cout << "Enter rows and columns of first matrix" << endl;
    cin >> m >> n;
    cout << "enter values into first matrix" << endl;
    vector<vector<int>> A;
    //first matrix input
    for (int i = 0; i < m; i++)
    {
        vector<int> temp;
        for (int j = 0; j < n; j++)
        {
            int i;
            cin >> i;
            temp.push_back(i);
        }
        A.push_back(temp);
    }
    cout << "Enter rows and columns of second matrix" << endl;
    cin >> a >> b;
    cout << "enter values into second matrix" << endl;
    vector<vector<int>> B;
    //second matrix input
    for (int i = 0; i < a; i++)
    {
        vector<int> temp;
        for (int j = 0; j < b; j++)
        {
            int i;
            cin >> i;
            temp.push_back(i);
        }
        B.push_back(temp);
    }

    bool k = check(n, a);
    if (k)
    {
        STRASSEN_algorithm(A, B, m, n, a, b);
    }
    else
    {
        cout << "martrix multiplication not possible";
    }
    return 0;
}

Applications

Generally Strassen’s Method is not preferred for practical applications for following reasons.

The constants used in Strassen’s method are high and for a typical application Naive method works better.
For Sparse matrices, there are better methods especially designed for them.
The submatrices in recursion take extra space.
Because of the limited precision of computer arithmetic on noninteger values, larger errors accumulate in Strassen’s algorithm than in Naive Method

Strassen’s Matrix Multiplication algorithm

matrix multiplication Algorithms Machine Learning (ML) strassen matrix multiplication

Pseudocode

Complexity

Implementations

C++

Applications

Russian peasant multiplication algorithm

Most commonly used utilities in Standard Template Library in C++