Russian peasant multiplication algorithm

Russian peasant multiplication is an interesting way to multiply numbers that uses a process of halving and doubling without using multiplication operator. The idea is to double the first number and halve the second number repeatedly till the second number doesn’t become 1. In the process, whenever the second number become odd, we add the first number to result (result is initialized as 0).

Explanation

The value of a×b is same as (a×2)×(b/2)

• for even values of b: a×b = (a×2)×(b/2).
• for odd values of b :a×b = ((a×2)×(b/2) + a).

In the while loop, we keep multiplying ‘a’ with 2 and keep dividing ‘b’ by 2. If ‘b’ becomes odd in loop, we add ‘a’ to ‘res’. When value of ‘b’ becomes 1, the value of ‘res’ + ‘a’, gives us the result.

Example:

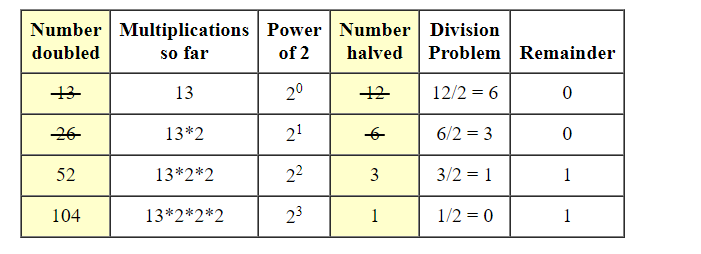
Let a and b be 13 , 12 .

Halving
for 12 :

• 12/2 = 6 remainder 0
  6/2 = 3 remainder 0
  3/2 = 1 remainder 1
  1/2 = 0 remainder 1.

Reading the remainders from bottom to top, we get 1100, so 12 in base two is 1100.

• 12 = 1100 (base 2)
  = 1×2^3 + 1×2^2 + 0×2 + 0×1
  = 23 + 22
  = 8 + 4.

By halving 12 repeatedly, we have broken it down into powers of two.

The Distributive Property

We are trying to multiply 12 by 13. We can break 12 down any way we like,

• 12×13
  = (4 + 8) × 13
  = (2^2 + 2^3) × 13
  = 2^2 × 13 + 2^3 × 13.

If we can multiply 13 by 2^2 and 2^3, we will be finished.

Doubling

when the number in the remainder column is 0, the corresponding row for Russian peasant multiplication is crossed out.

• 2^2 × 13 + 2^3 × 13 = 52 + 104 = 156, so 12 * 13 = 156.

Pseudocode

Let the two given numbers be 'a' and 'b'.
1) Initialize result 'res' as 0.
2) Do following while 'b' is greater than 0
   a) If 'b' is odd, add 'a' to 'res'
   b) Double 'a' and halve 'b'
3) Return 'res'. 

Complexity

• Worst case time complexity: Θ(logn)
• Space complexity: Θ(1)

Implementations

• C++

#include <iostream>
using namespace std;
unsigned int russianPeasant(unsigned int a, unsigned int b)
{
    int result = 0; 
    while (b > 0)
    {
        if (b & 1)
            result = result + a;	
        a = a << 1;
        b = b >> 1;
    }
    return result;
}
int main()
{
    unsigned int a,b;
    cout << "Enter two numbers to multiply" << endl;
    cin >> a >> b;
    cout << "product: "<< russianPeasant(a, b) << endl;
    return 0;
}