
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes
Imagine yourself to be the Vasco-Da-Gama of the 21st Century who have come to India for the first time. Now you want to visit all the World Heritage Sites and return to the starting landmark but then there is a budget constraint and you don't want your crew to repeat site. Seems pretty tough for an young exlplorer,right ?
This situation can be imagined as a classical Graph Theory problem where each heritage site is a "Vertex" and the route from one site to the other is an "Edge".
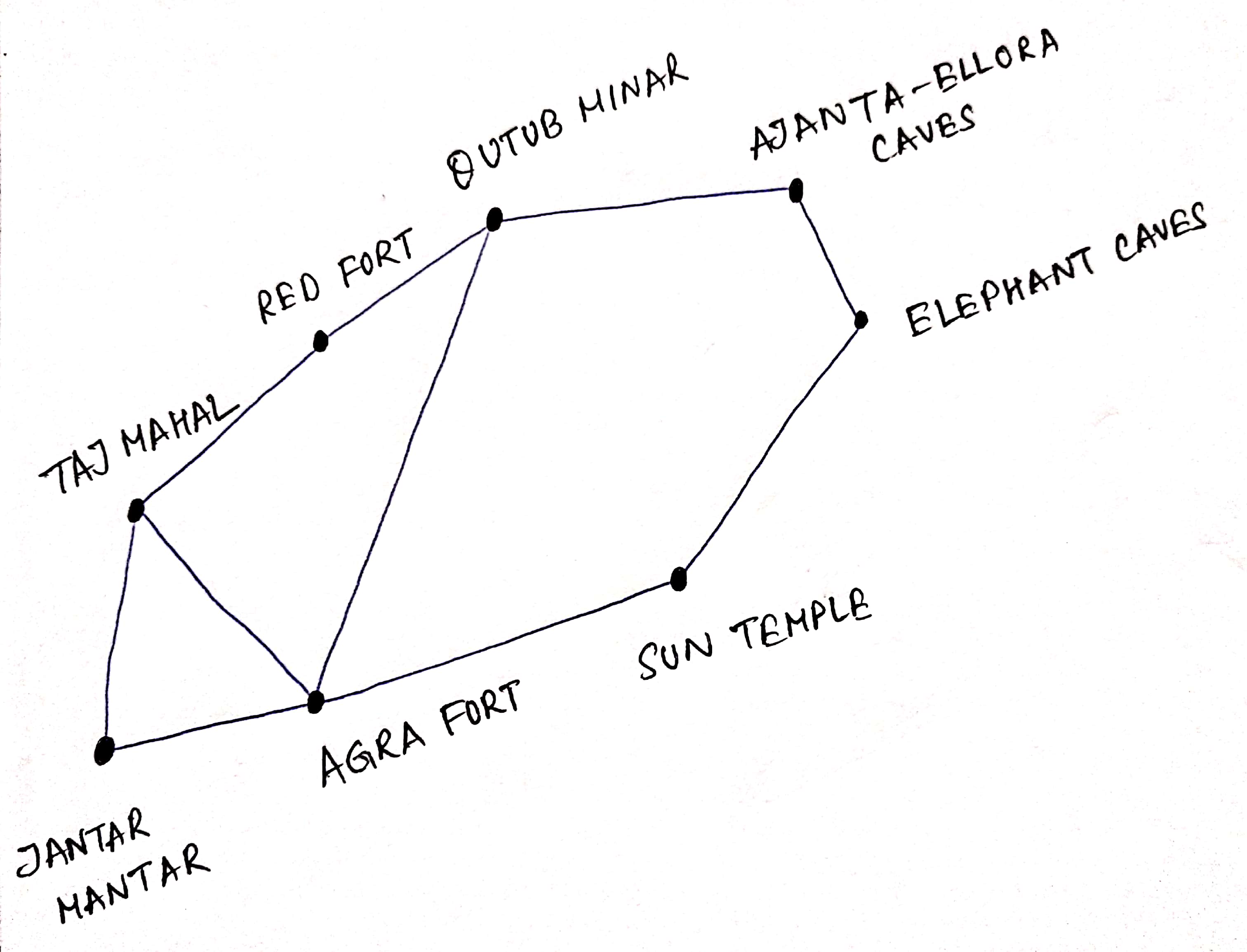
This route map of visiting every node and returning to the starting node is what called as a "Hamilton Cycle"
Definition
A Circuit in a graph G that passes through every vertex exactly once is called a "Hamilton Cycle".
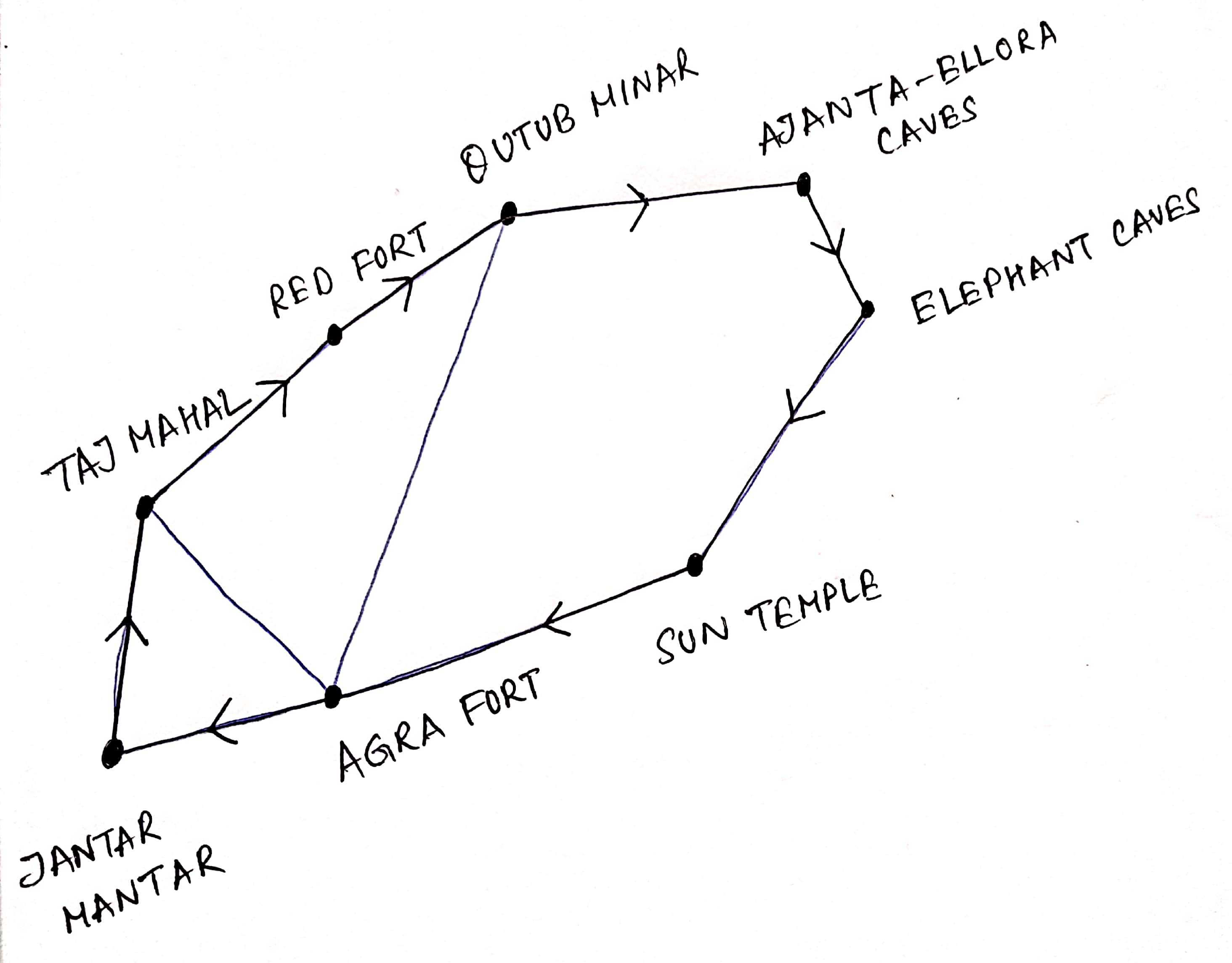
The route depicted starting from Taj Mahal and ending in there is an example of "Hamilton Cycle".
Algorithm
Data Structures used :
- A two dimensional array for the Graph named graph[][]
- A one dimensional array for storing the Hamilton Cycle named path[]
Step 1 : Insert vertex 0 (i.e the starting vertex) to the path[] array.
Step 2 : Check whether a vertex starting from (vertex 1) is adjacent to the previously added vertex and has been added.
Step 3 : If we find such a vertex satisfying conditions of Step 2, then we add that vertex to path[]
Step 4 : If we don't find such a vertex we return False
Example
Given a graph G, we need to find the Hamilton Cycle
Step 1: Initialize the array with the starting vertex
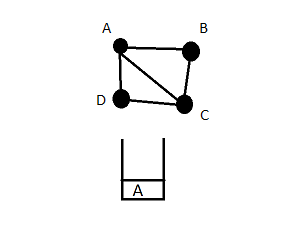
Step 2: Search for adjacent vertex of the topmost element (here it's adjacent element of A i.e B, C and D ). We start by choosing B and insert in the array.
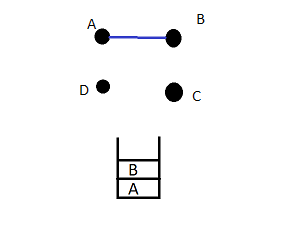
Step 3: The topmost element is now B which is the current vertex. We again search for the adjacent vertex (here C) since C has not been traversed we add in the list.
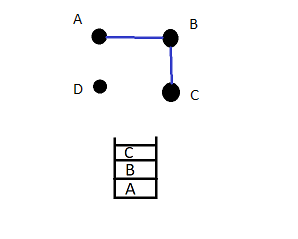
Step 4: The current vertex is now C, we see the adjacent vertex from here. We get D and B, inserting D into the array as B has already been considered.
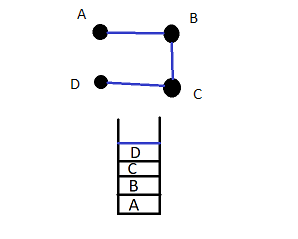
Step 5: The current vertex is now D since it is a Hamilton Cycle, we need to get back to the starting vertex (which is A). Thus a Hamilton Cycle of the given graph is A -> B -> C -> D -> A .
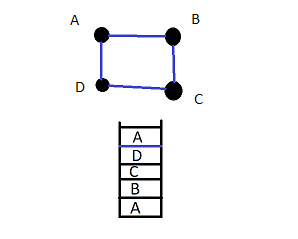
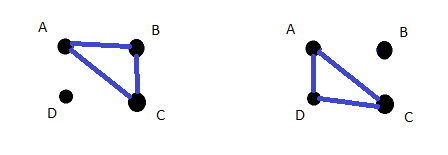
The Hamilton Path covering all the vertexes. Another Cycle can be A -> D -> C -> B -> A.
In another case, if we would have chosen C in Step 2, we would end up getting stuck. We would have to traverse a vertex more than once which is not the property of a Hamilton Cycle.
Code
#include<iostream>
#define NODE 4
using namespace std;
int graph[NODE][NODE];
int path[NODE];
void displayCycle() { //Function to display the cycle obtained
cout<<"The Hamilton Cycle : " << endl;
for (int i = 0; i < NODE; i++)
cout << path[i] << " ";
cout << path[0] << endl; //print the first vertex again
}
bool isValid(int v, int k) {
if (graph [path[k-1]][v] == 0) //if there is no edge
return false;
for (int i = 0; i < k; i++) //if vertex is already taken, skip that
if (path[i] == v)
return false;
return true;
}
bool cycleFound(int k) {
if (k == NODE) { //when all vertices are in the path
if (graph[path[k-1]][ path[0] ] == 1 )
return true;
else
return false;
}
for (int v = 1; v < NODE; v++) { //for all vertices except starting point
if (isValid(v,k)) { //if possible to add v in the path
path[k] = v;
if (cycleFound (k+1) == true)
return true;
path[k] = -1; //when k vertex will not in the solution
}
}
return false;
}
bool hamiltonianCycle() {
for (int i = 0; i < NODE; i++)
path[i] = -1;
path[0] = 0; //first vertex as 0
if ( cycleFound(1) == false ) {
cout << "Solution does not exist"<<endl;
return false;
}
displayCycle();
return true;
}
int main() {
int i,j;
cout << "Enter the Graph : " << endl;
for (i=0;i<NODE;i++){
for (j=0;j<NODE;j++){
cout << "Graph G(" << (i+1) << "," << (j+1) << ") = ";
cin >> graph[i][j];
}
}
cout << endl;
cout << "The Graph :" << endl;
for (i=0;i<NODE;i++){
for (j=0;j<NODE;j++){
cout << graph [i][j] << "\t";
}
cout << endl;
}
cout << endl;
hamiltonianCycle();
}
Input and Output
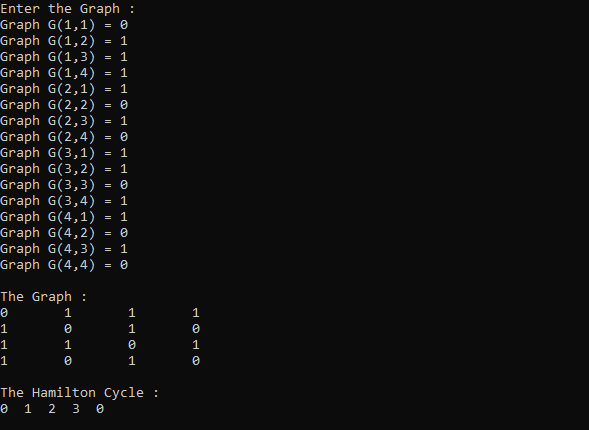
The Graph given in the example section, we input that in the form of an Adjacency Matrix. The Hamilton Cycle thus obtained is the output.
INPUT :
Graph :-
0 1 1 1
1 0 1 0
1 1 0 1
1 0 1 0
OUTPUT :
The Hamilton Cycle :
0 -> 1 -> 2 -> 3 -> 0
Complexity
The Worst Case complexity when used with DFS and backtracking is O(N!).
Practical Applications
- Hamilton's "A Voyage Round The World Puzzle"
Inspired from a game called the "Isconian puzzle", a dodecahedron containing 20 vertices which denotes a city and the edges denotes the routes (as shown in the Fig. (a)). The object of the puzzle was to start at a city and travel along the edges of the dedecahedron, visiting each of other 19 cities exactly once and end back at the first city.
The cycle or the circuit thus obtained is (Fig. (b)):

- The Travelling Salesman Problem
This problem involves finding the shortest route a travelling salesman should take to visit a set of cities. This reduces to finding a "Hamilton Cycle" in a complete graph such that the total weight of its edges is as small as possible. This shortest can be found out by something called the Dijkastra Algorithm
