In this article, we will discuss the problem K-th largest Element in a stream, and understand the different methods that can be used to solve the problem efficiently.

Table of content:

1. Problem Statement
2. Approach 1: Sorting the Array
3. Approach 2: Using min-heap

We will dive into the problem now.

Problem Statement

Design a class to find the kth largest element in a stream. Note that it is the kth largest element in the sorted order, not the kth distinct element.

Implement KthLargest class:

• KthLargest(int k, int[] nums) Initializes the object with the integer k and the stream of integers nums.
• int add(int val) Appends the integer val to the stream and returns the element representing the kth largest element in the stream.

Let us understand the question first.

We are given a stream of numbers and we need to find the Kth largest value in that stream.

But, what does Kth largest Value mean?

Consider this example

In the above array, there are 10 integers lets try to find the 4th largest value in this array. So let's just arrange the elements of the array in descending order and find the fourth value. Yes, that's the 4th largest value in the array.

Similarly, we are required to find the kth largest value in a given stream of integers.

We will solve this problem in two methods.

1. By sorting the array
2. Using Min heap

Approach 1: Sorting the Array

In this method, we sort the stream of integers after adding a new value to it each time and then we access the required largest element and return it.

Steps

1. Add the new element into the array
2. sort the array
3. Find the Kth element from the last of the sorted array and return it.

class KthLargest:

    def __init__(self, k: int, nums: List[int]):
        self.k = k
        self.nums = nums

    def add(self, val: int) -> int:
        self.nums.append(val)
        return sorted(self.nums)[-1 * self.k]

You may wonder why we are implementing this through a class? It is because we are dealing with a stream of numbers hence using a class makes it convenient for us to add the numbers to the stream and find the Kth largest number in it.

We can see two methods in this class, the first init method is used to initialize the class with the initial stream of numbers nums and the value of k.

The second method is where we find the Kth largest number in the stream. This method takes a number val which is to be added to the stream. And then we append the integer val to the stream. And then we sort the elements in the array nums, now we access the kth element from the end of the array which will give us the Kth largest element in the array, and we return it.

Complexity of this method

In this method, we are sorting the array each time, thus the time complexity of this method is O(n), where n is the number of elements in the array.

The space complexity of the algorithm is O(n).

The runtime and memory for solving the problem using this method are given below.

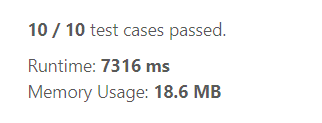
We can see that this runtime is extremely high and sometimes it may exceed the time limit of the problem too.

Approach 2: Using min-heap

Using min-heap is a much more efficient way to solve the problem, we will see that in a bit. But, before we start solving the problem using a min-heap, let's quickly recall what a min-heap is.

A min-heap is a binary tree data structure, where the parent node is smaller than its child nodes.

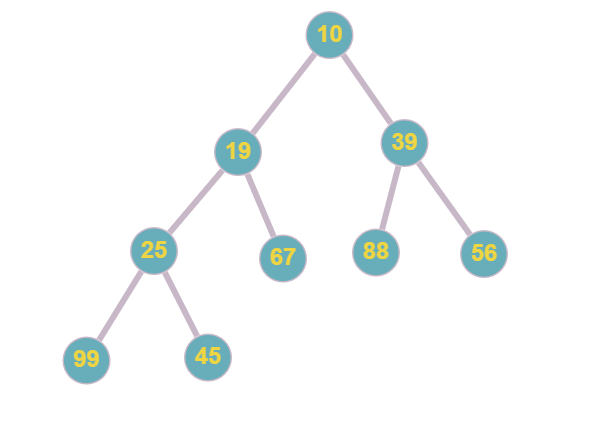
The above image is an example of a min-heap.

The most important thing to understand in min-heap is that the child nodes are greater than the parent node. As a result of this, the root node holds the smallest value of the heap and the end node holds the largest value of the heap.

But how can we use this min-heap to solve our problem? In our question, we are asked to return the Kth largest number in the stream, which means there are k-1 numbers larger than our answer, and the rest of the numbers which are smaller than the Kth largest number do not matter.

So, we create a min-heap of size k i.e. containing the k largest elements of the stream. So the root node will always have our Kth Largest element of the stream. Thus, the only thing we need to do is keep the min-heap updated with K largest numbers and we can retrieve our Kth largest number quickly from the root node, let's see how we can do this with the code.

Steps

1. Create a class for the min-heap data structure ( here built-in functions are used to do the heap operations )
   • Create a method to initialize the min-heap
   • Create a method to push an element into the min-heap
   • Create a method to return the root node i.e. the K the largest number
2. Get the input array and the value of k.
   • Update the min-heap with the values of the input array
   • Then get the values to be added into the stream
   • Return the root node of the min-heap

from heapq import heappush , heappop

class minHeap:

    # Initializes the heap
    def __init__(self, k):
        self.heap = []
        self.size = k

    # a method to push elements into the min heap
    def push(self, val):

        # pushs the elements into the minHeap if the heap size is less than k
        if len(self.heap) < self.size  :
            heappush(self.heap,val) 

        # push the element into the heap if it is greater than the root node
        elif val > self.heap[0] :
            heappop(self.heap)
            heappush(self.heap,val)

    # a method to return the root node
    def ans(self):
        return self.heap[0] 

class KthLargest:

    def __init__(self, k: int, nums: list[int]):
        self.nums = minHeap(k)
        self.k = k
        for i in nums:
            self.nums.push(i)

    # a method to add elements into the stream and return the Kth largest value
    def add(self, val: int) -> int:
        self.nums.push(val)

        return self.nums.ans()

Phew, I know this code looks a bit messy, but don't worry let's break it down and we will understand everything.

First, let's deal with the minHeap class. This class has 3 methods,

1. The first method initializes the minHeap class with an array to store the values of the heap and the maximum size of the heap i.e. the value of k.
2. The second method push() is used to push the elements into the min-heap and keep the min-heap updated with the K largest numbers of the stream.
   1. The first if statement pushes anything into the heap if the size of the heap is less than k.
   2. The elif statement checks if the element passed into the stream is greater than the root node i.e. the kth largest element so far, if it is greater than it, it pops out the element in the root node and pushes the new element into it. Doing so the min-heap gets updated and the new Kth largest number will be at the root node.

Note: If you don't understand how the pushing and popping of elements in the min-heap take place, feel free to refer to this article.

3. The third method ans() is a simple method that returns the root node of the min-heap.

Now coming to the KthLargest Class, since the min-heap class does all the calculations we need to find the kth largest number in the stream, we just need to pass values into the min-heap and return the answer in this Class

The first method initializes the KthLargest class with the value of k and the min-heap that will be used to find the kth largest number in the stream. And then we use a for loop to add the initial elements of the stream into the min-heap.

The second method add() is used to get the new elements of the stream and return the Kth largest element in the stream. Here, we just use the push() method from the min-heap class to update the min-heap with the new number.

And then finally, we use the ans() method to return the root node i.e. the Kth largest element in the stream.

Complexity of the algorithm

You may wonder why to go through the pain of creating a min-heap and pushing elements to it, while we can just sort the array stream and return the Kth largest element.

The reason is speed. The time complexity of the operations in a min-heap is O(log k), Thus reducing the time taken for finding the Kth largest value exponentially and this makes our algorithm really fast.

The space complexity of this approach is O(k).

The runtime and memory of this approach is given below

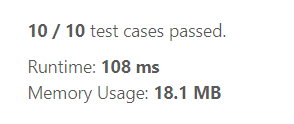
When we compare this runtime with the runtime of the brute force approach we can see that this is nearly 70x times faster than that.

Conclusion

Every problem can be solved in multiple ways, but always opt for the one that has the best time & space complexity and is faster than the other solutions. With this article at OpenGenus, you must have the complete knowledge of finding the k-th largest element in a stream of numbers.