Karger’s algorithm to find Minimum Cut

In this article, we will explore how the Karger's algorithm works to find the minimum cut in a graph and its C++ implementation. This is a randomized algorithm based on Graphs.

Table of contents:

1. What is the minimum cut?
2. Karger's Algorithm
3. Success Probability and Time complexity
4. Code Implementation of Karger's algorithm

Pre-requisite: Randomized algorithm, Minimum Cut

Let us get started with Karger’s algorithm to find Minimum Cut.

What is the minimum cut?

The minimum cut in a graph refers to the number of edges in the graph that must be disconnected to split the graph into two disjoint components. Let's take a few pictorial examples to get a more clearer idea.

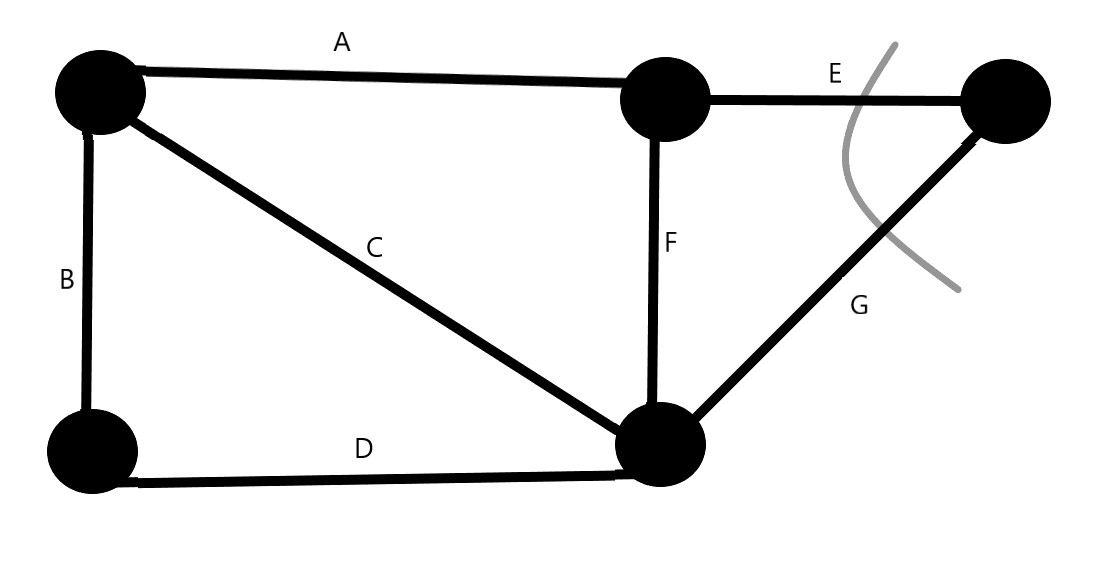
In this example, the minimum cut is going to be the severing of the edges E and G. So, Minimum cut=2.

The minimum cut can also achieved by severing the edges B and D.

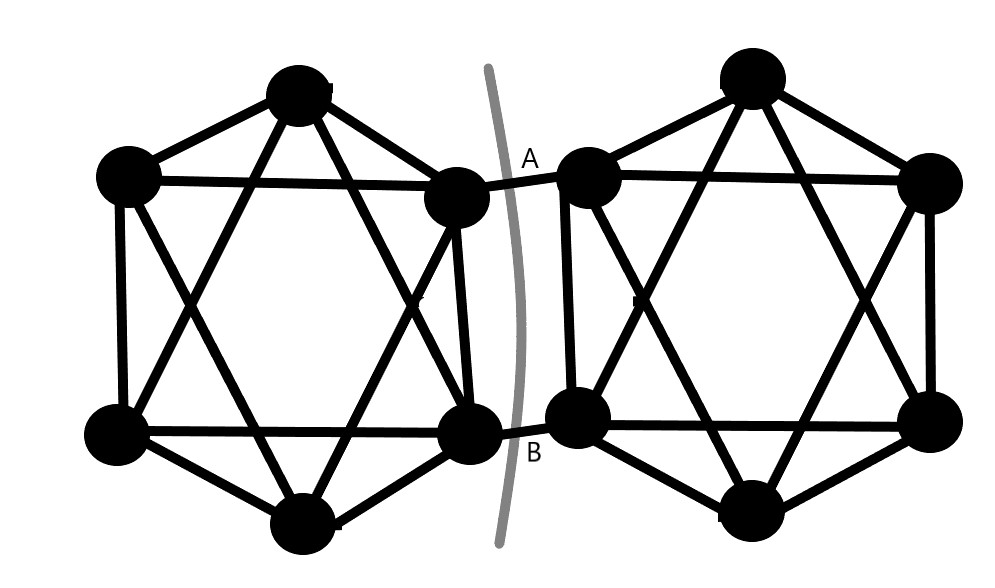
In this example, we see that the minimum cut is achieved by severing the edges A and B, which breaks the graph into two symmetric halves. So, Minimum cut=2.
We see that the size of the two disjoint components does not matter to us i.e. the two components can vary largely in size or be almost equivalent.

Karger's Algorithm

Karger's algorithm is a randomized algorithm to find the minimum cut in an unweighted and undirected graph in which we pick up a random edge and contract or coalesce the two ends of edge into a single point. So, all points eventually combine into super-nodes and the size of the graph keeps decreasing. All the while, all self loops are removed. At the end of the algorithm, we are left with two nodes connected by a number of edges. The number of edges connecting the two final super-nodes gives the required minimum cut.

So, we have the following algorithm:

While there are more than 2 vertices-
      a) Pick a random edge (x, y) in the contracted graph.
      b) Merge the points x and y into a single vertex (update the contracted graph).
      c) Remove self-loops.

Return cut represented by two vertices.

Let us go back to our first example and see this algorithm in action visually.

• So, in the first step, we merge the vertices at the ends of edge B. So, we end up with a super node which now becomes one end of the edges A, C & D. The edge B will form a self-loop since both of its ends have converged. So, we omit it.

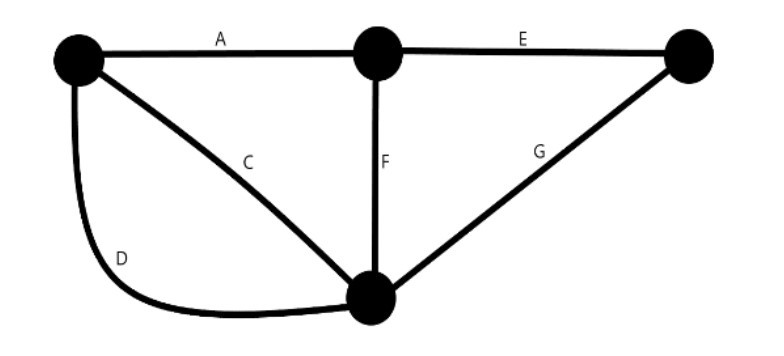
• We contract the edge C (or D, same meaning). Both the edges C and D will form self loops and are thus omitted. We now have a super node which becomes the other end point of the edges A and F.

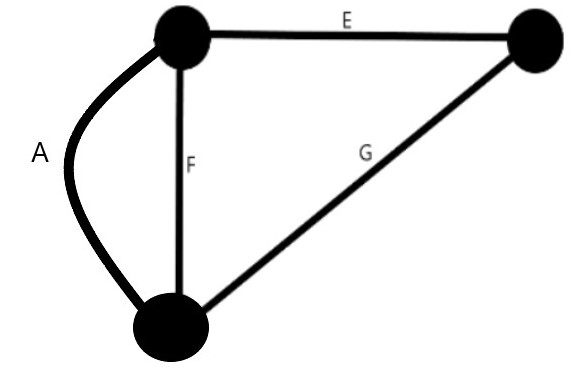
• We pick the edge A (or F) and converge the points at either end. So, both A and F form self loops and are removed from the graph. We end up with a graph with two vertices connected by the edges E and G.

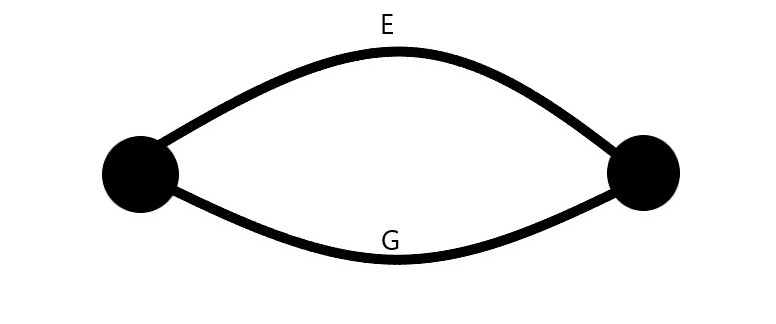
Since only two vertices remain, the algorithm terminates and 2(the number of edges remaining in the graph) is returned as the minimum.

Success Probability and Time complexity

Since Karger's algorithm is a randomised algorithm, it doesn't always arrive at the right answer in the first run. In fact, the probability of reaching the minimum cut is 2/n(n-1), which is low. So to ensure the minimum cut, we must run the algorithm an adequate number of times. It has been observed that we need atleast n² log(n) runs to arrive at the optimal solution, where n is the number of vertices in the graph.

The time complexity for merging of any pair of vertices as well as removal of self loops is O(n). Since both of these will be done on the graph until only 2 vertices remain, the time complexity for a single run is O(n²). But for optimality, we will be running the algorithm n² log(n) times, so our overall complexity shoots up to O(n⁴ log(n)).

Code Implementation of Karger's algorithm

In the c++ implementation, we will be using an adjacency matrix to store the graph. This will be defined as a vector of vectors vector<vector<int>> edges. The number of rows and columns in the matrix is equal to the number of vertices in the graph vertices. We shall make some set and get functions to set values in the graph and retrieve them as well. We also have get and set functions for matrix size.
Apart from these, we have three major functions essential for the algorithm- remove_self_loops(), merge_vertices() and kargers_algorithm(). Let us see these functions one by one.

• The remove_self_loops() iterates through the graph and removes all self loops i.e. edges that start and end at the same vertex. Since we are using an adjacency matrix, this function will set all the diagonal elements as 0.

graph& remove_self_loops(){
        for(int i=0;i<vertices;i++){
            set(i,i,0);
        }
        return *this;
   }

We will see the set() function definition later when we examine the entire program.

• The merge_vertices() function takes two parameters u and v which are the vertices to be merged. The function iterates through the graph and for every vertex i, it adds all its edges (i,u) to the vertex v and then, sets edges of vertex u to 0. This is also done for all (u,i) pairs as well since the graph is undirected.

graph& merge_vertices(int u, int v){
   if(u< vertices && v< vertices){
        for(int i=0;i<vertices;i++){
            set(i,v,get(i,u)+get(i,v));
            set(i,u,0);
            set(v,i,get(u,i)+get(v,i));
            set(u,i,0);
          }
   }
   return *this;
   }

• Now, we come to our kargers_algorithm() function. This function iterates while there are more than two vertices in the graph where it picks any two vertices at random, merges them and removes self loops. So, we have the code:

void kargers_algorithm(graph& g)
{
   g.remove_self_loops();
   while (g.count_vertices() > 2)
   {
      int u = 0, v = 0;
      do
      {
         u = rand() % g.get_size();
         v = rand() % g.get_size();
      }
      while (g.get(u, v) == 0);
   // Merge both vertices
      g.merge_vertices(u, v);
   //Remove self-loops
      g.remove_self_loops();
   }
   return;
}

The function defines only one run of the algorithm. So, for optimality, we will call it multiple times in our main() function.
Now, we can see the final code with a graph class and all of its member functions and see how it all comes together:

#include <bits/stdc++.h>
using namespace std;

class graph{
public:
    int vertices;
    vector<vector<int>> edges;

   void set(int r, int c, int d) {
       edges[r][c] = d;
       return;
       }
   int get(int r, int c) {
       return edges[r][c];
       }

   void set_size(int s) {
       vertices = s;
       edges.resize(vertices * vertices);
       return;
       }
   int get_size(){
       return vertices;
       }
   int count_vertices() {
        int v=0;
        for(int i=0;i<vertices;i++){
             for(int j=0;j<vertices;j++){
                if(get(i,j)>0){  
                v++; break;
                }
            }
        }
        return v;
   }
   int count_edges(){
        int e=0;
        for(int i=0;i<vertices;i++){
            for(int j=0;j<vertices;j++){
                e+=get(i,j);
            }
        }
        return e/2;
   }

   graph& remove_self_loops(){
        for(int i=0;i<vertices;i++){
        set(i,i,0);
        }
        return *this;
   }

   graph& merge_vertices(int u, int v){
   if(u< vertices && v<vertices){
        for(int i=0;i<vertices;i++){
            set(i,v,get(i,u)+get(i,v));
            set(i,u,0);
            set(v,i,get(u,i)+get(v,i));
            set(u,i,0);
          }
   }
   return *this;
   }
};
void kargers_algorithm(graph& g)
{
   g.remove_self_loops();
   while (g.count_vertices() > 2)
   {
      int u = 0, v = 0;
      do
      {
         u = rand() % g.get_size();
         v = rand() % g.get_size();
      }
      while (g.get(u, v) == 0);
   // Merge both vertices
      g.merge_vertices(u, v);
   //Remove self-loops
      g.remove_self_loops();
   }
   return;
}
int main()
{
     graph g;
     g.vertices=6;
     g.edges={{0 ,1 ,0, 1, 1, 0},
              {1, 0, 1, 0, 1, 0},
              {0, 1, 0, 0, 1, 1},
              {1, 0, 0, 0, 1, 0},
              {1, 1, 1, 1, 0, 1},
              {0, 0, 1, 0, 1, 0}};
      graph ming; ming.set_size(0);

      cout << "Input vertex count: " << g.count_vertices() << endl;
      cout << "Input edge count: " << (g.count_edges()) << endl;

      int n = g.count_vertices();
      float ln = log((float) n);
      float runs = n * n * ln, mincut = INT_MAX;

      for (int i = 0; i < runs; ++i)
      {
         graph copy = g;
         kargers_algorithm(copy);
         int cut = copy.count_edges();
         if (cut < mincut)
         {
            mincut = cut;
            ming = copy;
         }
      }
      cout << "Output vertex count: " << ming.count_vertices() << endl;
      cout << "Output edge count: " << ming.count_edges()<< endl;
    cout<< "Minimum cut for the graph is "<< mincut<<endl;
    return 0;
}

In the main function, we have calculated the number of runs =n² log(n) using appropriate data types. We initialise a new graph ming to store the graph which has the minimum cut. We also create a graph copy, which is initialised to our given graph g. This copy is modified by the algorithm to give the minimum cut. If the cut reached is lower than the current minimum cut mincut, then the mincut value is updated and the graph ming stores the minimum cut graph.
Output:

Input vertex count: 6
Input edge count: 9
Output vertex count: 2
Output edge count: 2
Minimum cut for the graph is 2

Thus, in this article at OpenGenus, we have explored what the minimum cut for graphs is, Karger's algorithm for finding out the same as well as its C++ implementation. Keep learning!