Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored an insightful approach/ algorithm to find the maximum number of points on a straight line. This problem finds many uses in computational geometry.
TABLE OF CONTENTS
- PROBLEM STATEMENT DEFINITION
- SOLUTION ANALYSIS
- METHOD-1 NAIVE ALGORITHM
- Approach
- Algorithm
- Pseudocode
- Complexity
- METHOD-2 USING MAPS
- Approach
- Algorithm
- Pseudocode
- Complexity
- COMPARISON OF APPROACHES
- APPLICATIONS
Pre-requisite: Computational Geometry
Let us get started with Maximum points on a line.
PROBLEM STATEMENT DEFINITION
Given N point on a 2D plane as pair of (x, y) co-ordinates, we need to find maximum number of point which lie on the same line.
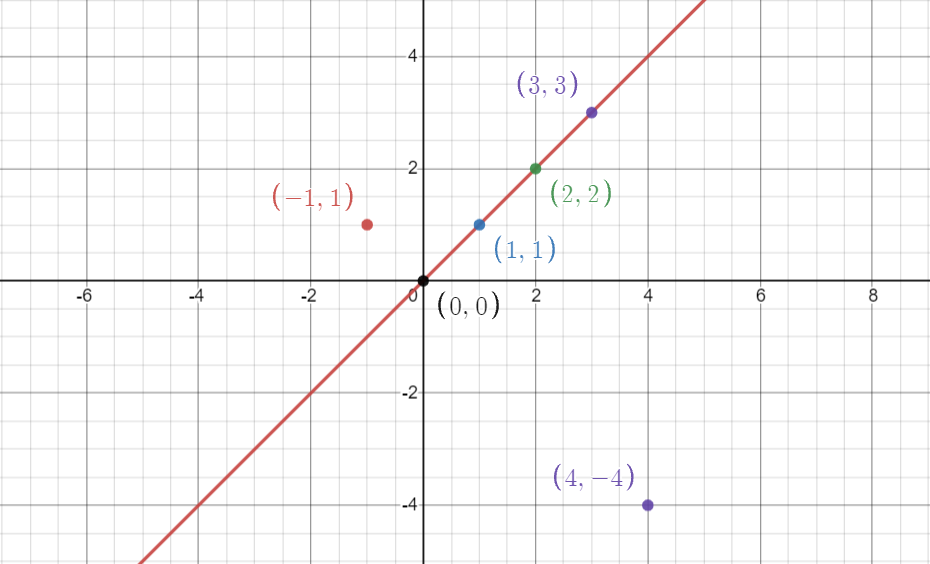
EXAMPLE-1
Input : points[] = {2,2}, {4, -4}, {1, 1}, {0,0}, {3, 3}, {-1, 1}
Output : 4
Explanation: Then maximum number of point which lie on same line are 4. Those point are {0, 0}, {1, 1}, {2, 2} and {3, 3}
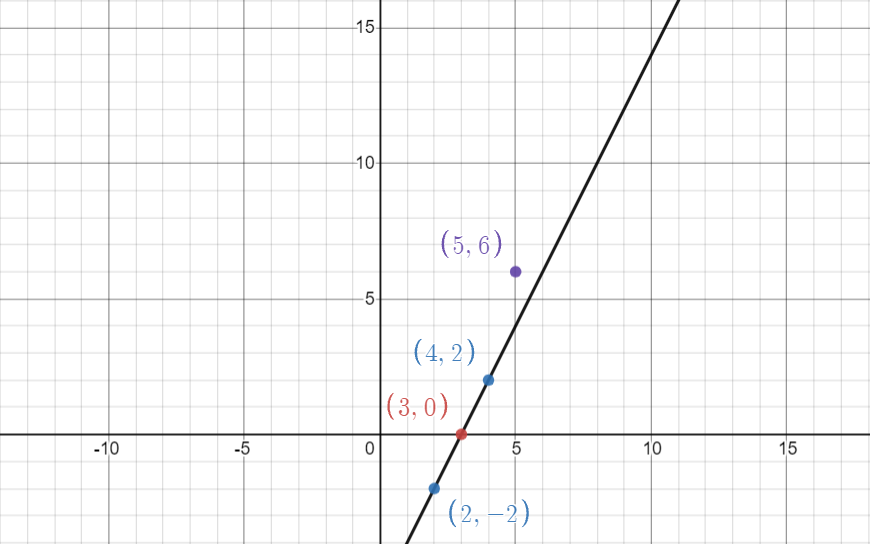
EXAMPLE-2
Input: points = {3,0}, {4,2}, {2,-2}, (5,5}
Explanation: The maximum number of point which lie on same line are 3, those points are {3,0}, {4,2} and {2,-2}.
SOLUTION ANALYSIS
First of all, how do we know the points are on the same line? It is clear from the graphs above that the answer is slope!
The slope of a line can be computed using any two points (x1,y1) (x2,y2) on the line:
slope = (y2-y1)/(x2-x1) , where x2 is not equal to x1.
In this problem, we want to know the maximum number of points on one line. Two point determine a line and its slope. The solution lies in the fact that for every single point, all the possible lines (slopes) which passes through this point and any other point can be easily computed.
If one point is now fixed, traversing through every other point can get all the lines with one common point, so if two lines line_AB and line_AC have same slope, points A, B and C are actually on the same line.
Note: The advantage of using a common point for calculating the slopes is that it nullifies the risks of finding parallel lines(which have the same slope). Care must be taken however to not include duplicate points.
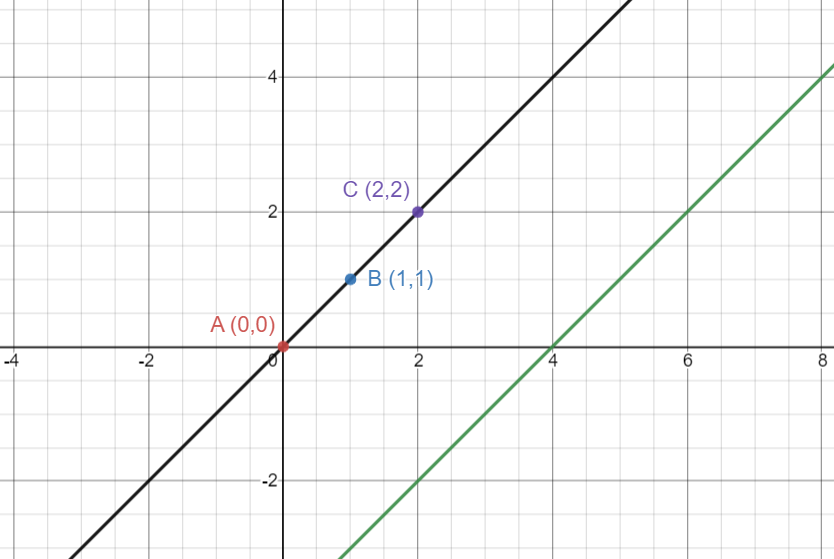
In the example below, if point A is (0,0) point B is (1,1) and point C is (2,2), we can start from point A (0,0) and calculate the slope wrt point B (1,1). Storing this slope, we can find the slope of AC and compare with the stored value. as they are equal, they lie on the same line. Note that the green line parallel to the common line has the slope but we can discard its influence using the common point idea.
This is the basic idea common to all approach to be discussed henceforth. The only difference lies in calculation of slopes and storing and comparing the various values. We have two approaches to solve this problem.
- Method-1 Naive Algorithm
- Method-2 Using Maps
METHOD-1 NAIVE ALGORITHM
Also called the brute force approach, this is the most trivial solution to this problem. It involves the most time-complex solution where for every pair of points, we check how many other points are collinear (lie in the same line) with them and maintain track of it.
Approach
To compute the number of points on a line:
- Take any two points and calculate the slope and store it.
- Fix one of the two points for further steps.
- Calculate the slope of the common point with all other points and compare with stored slope.
- Initialize a counter variable to count the number of points whose slope matches with the stored slope.
- Repeat the first four steps for all points comparing the new count with the previous count and store the maximum of the two.
Also note that two points could coincide (or duplicate points could be present). We have to ignore the second instance such points.
Algorithm
- Find the slope of any two points and store it
- Keep one of the points common for further steps
- For every other non-coinciding point, check if it is collinear with those two points by comparing slope of the common point and new point with the stored slope
- Maintain a counter that will store the maximum number of points that will be lying on the same line.
Pseudo Code
int same_line(int a[],int b[],int c[]){
if (a[0]-c[0])*(b[1]-c[1]) == (a[1]-c[1])*(b[0]-c[0])
return 1
else
return 0
}
int maxPoints(int[][] points) {
int n = points.size()
int counter = 0
for(int i = 0 to i < n){
for(int j = i+1 to j < n){
if(points[i][0]==points[j][0] && points[i][1]==points[j][1])
continue
int sum = 0
for(int k = 0 to k < n)
sum += same_line(points[i],points[j],points[k])
counter = max(max_pts,sum)
}
}
if(counter==0)
return n
else
return max_pts
}
Implementation
Let us have a look at the C++ program implementing this approach
#include <bits/stdc++.h>
using namespace std;
int coline(int a[],int b[],int c[]){
if ((a[0]-c[0])*(b[1]-c[1]) == (a[1]-c[1])*(b[0]-c[0]))
return 1;
else
return 0;
}
int main(){
int points[6][2]={{-1, 1}, {0, 0}, {1, 1}, {2, 2},{3, 3}, {3, 4}};
int n=6;
int max_pts = 0;
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
if(points[i][0]==points[j][0] && points[i][1]==points[j][1])
continue;
int sum = 0;
for(int k=0;k<n;k++)
sum += coline(points[i],points[j],points[k]);
max_pts = max(max_pts,sum);
}
}
if(max_pts==0)
max_pts=n;
cout<<"The maximum number of points on the same line: "<<max_pts;
return 0;
}
OUTPUT:
The maximum number of points on the same line: 4
Time-Complexity
Since there are 3 nested loops which run from almost 1 to n, the time complexity is n^3
- Worst case time complexity:
Θ(n^3) - Average case time complexity:
Θ(n^3) - Best case time complexity:
Θ(n^3)
Space-Complexity
We do not use any extra space and hence the Space complexity is: Θ(1)
METHOD-2 USING MAPS
As mentioned earlier, when we pick two points one by one from the set of distinct points and find slopes for every other point, we remove the possibility of parallel lines from each iteration. The only downside is that we need to manually compare the slopes for every pair and if any other slope is the maximum, we need to change the counter and the stored slope and again compare manually.
Maintaining a hash map of slopes will help us identify the maximum number of points lying on the same line easily by reducing the searching cost.
Pseudo Code
int maxPoints(int points[][]) {
int max_count = 0
for (int i = 0 to i < points.size()) {
int localmax = 0, overlap = 1, vertical = 1;
map<double, int> m
for (int j = i + 1 to j < points.size()) {
if (points[i][0] == points[j][0] && points[i][1] == points[j][1])
overlap = overlap + 1
else
if (points[i][0] == points[j][0])
vertical = vertical + 1
else {
slope = double(points[i][1] - points[j][1]) / (points[i][0] - points[j][0])
m[slope] = m[slope] + 1
}
}
for (slope in m)
localmax = max(m[slope], localmax)
max_count = max(vertical, max(localmax + overlap, max_pts))
}
return max_count
}
Algorithm
- For each point, find the slope from that point to every other point.
- Create an ordered-map and store the total number of collinear points against the slope.
- To maintain the precision level treat the slope as pair ((y2 – y1), (x2 – x1)) instead of ratio and reducing the pair by their gcd before inserting into map.
NOTE An easier albeit naive way to achieve precision is to use double instead of float to calculate any ratio.
- To manage edge cases, create another variable to check for repeating points and create a vertical variable to count the number of points lying on the same vertical line.
- Lastly, maintain a max_count variable to store the maximum number of points lying on the same line
Implementation
Let us have a look at a PYTHON implementation of the algorithm
class Point:
def __init__(self, a=0, b=0):
self.x = a
self.y = b
class Solution:
def maxPoints(self, points):
if (len(points)<=2):
return len(points)
max_points = 0
for i in range(0, len(points)):
l = {}
dup = 1
for j in range(0, len(points)):
if (points[i].x==points[j].x and points[i].y==points[j].y and i!=j):
dup+=1
elif i!=j :
if (points[i].x==points[j].x):
l['v'] = l.get('v',0) + 1
elif (points[i].y==points[j].y):
l['h'] = l.get('h',0) + 1
else: #regular slope
slope = 1.0*(points[i].y-points[j].y)/(points[i].x-points[j].x)
l[slope] = l.get(slope,0)+1
if (len(l)>0):
max_points = max(max_points,max(l.values())+dup)
else:
max_points = max(max_points,dup)
return m
Implementing the algorithm using C++
#include <bits/stdc++.h>
#include <vector>
using namespace std;
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
int maxPoints(vector<vector<int>> & points) {
int max_count = 0;
int n = points.size();
if(n < 3)
return n;
for(int i = 0;i<n;i++){
map<pair<int,int>, int> mp;
for(int j = 0;j<n;j++){
if(i != j){
int dy = (points[j][1] - points[i][1]);
int dx = (points[j][0] - points[i][0]);
int g = gcd(dy,dx);
mp[{dy/g,dx/g}]++;
}
}
for(auto p : mp){
max_count = max(max_count,p.second);
}
}
return max_count+1;
}
int main(){
vector<vector<int>> arr={{-1, 1}, {0, 0}, {1, 1}, {2, 2},{3, 3}, {3, 4}};
cout<<"The number of points on a common line is: " <<maxPoints(arr);
return 0;
}
OUTPUT:
The maximum number of points on the same line: 4
Time-Complexity
Since we have 2 nested loops running from 1 to n (number of points) the time-complexity is n^2. In the inner loop we have a gcd function which is executed in logn time.
Therefore, the overall time complexity of this algorithm is:
- Worst case time complexity:
Θ(n^2 * log n) - Average case time complexity:
Θ(n^2 * log n) - Best case time complexity:
Θ(n^2 * log n)
Space-Complexity
We use extra 'n' space in the mapping algorithm to store and compare the slopes of n points and hence the overall space complexity is: Θ(n)
COMPARISON OF APPROACHES
| Complexity | Naive Approach | Mapping Slopes Approach |
|---|---|---|
| Time-Complexity | n^3 | n^2 * log n |
| Space Complexity | 1 | n |
APPLICATIONS
- An advanced algorithm based on the same premise as this problem is used to launch missiles.
- It is used used in other computational geometry problems.
Question
Which approach is the most time-efficient for finding the maximum number of points in a line
Θ(n^3) The time-complexity of Mapping-Slopes approach is Θ(n^2 * logn)
With this article at OpenGenus, you must have the complete idea of solving maximum number of points on a line problem efficiently.