
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have presented Karp's Minimum Mean Cycle Algorithm along with C++ Implementation. Karp's theorem and Complexity Analysis.
Table of contents:
- Problem statement with example
- Theorem given by Karp
- Karp's Minimum Mean Cycle Algorithm
- Implementation
- Complexity Analysis
- References
Problem statement with example
In 1978 , Richard M. Karp gave a characterization of Minimum Mean Cycle. Given a strongly connected digraph, G(V,E) with n vertices consisting of non-negative weights. Mean Weight of a directed cycle defined as summation of edge weights of all edges present in a cycles over number of edges present in a cycle. Our task is to find Minimum Mean Cycle over all directed cycles present in a digraph.
Example :
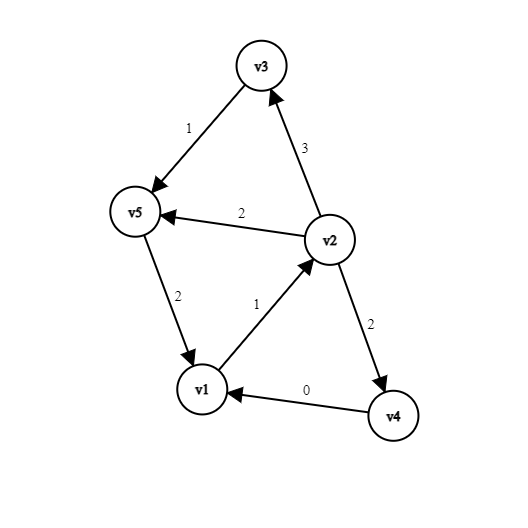
In a given directed graph, 3 directed cycles are possible and their following mean weight are as shown :
| Cycles | Path | Mean Weight |
|---|---|---|
| C1 | v1->v2-v4->v1 | (1+2+0)/3 |
| C2 | v1->v2->v5->v1 | (1+2+2)/3 |
| C3 | v1->v2->v3->v5->v1 | (1+3+1+2)/4 |
Theorem given by Karp
Let s be an arbitrary start vertex of G and λ* be Minimum Mean Weight over all all directed cycles.For each vertex v ∈ V and non-negative integer k , let Fk(v) be the minimum weight of any edge progression of length exactly k from s to v, of ∞ if no such edge progression exists. λ* can be defined as
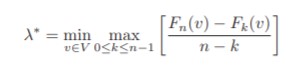
Proof
It can be observed that if each edge weight is reduced by constant c then λ* is also reduced by c. RHS of above equation is also reduced by c as F(v) is reduced by c and Fk(v) reduced by k*c. Let translation constant be such that λ* becomes zero.
If λ*= 0 then (Fn(v) - Fk(v))/(n-k) = 0 for some value of v and k. It is known that graph doesn't consists of negative edges and there exists a cycle of weight zero . Hence , we can say that there is an edge progression of edge length k less than n ,from vertex s to v having minimum-mean weight,Fn(v) >= min0<=k<n Fk(v). It implies that max0<=k<n(Fn(v) - Fk(v)) >= 0 . On dividing n-k on both sides, it can be deduced to max0<=k<n(Fn(v) - Fk(v))/(n-k)>= 0.
Above condition λ*= 0 holds if and only if Fn(v) = min0<=k<n Fk(v) for some vertex v which can be proved simply by assuming cycle C and repeating over and over until its path length becomes n and k.
For more details, refer to [1].
Karp's Minimum Mean Cycle Algorithm
Terminology
|E| = Number of edges present in a graph
|V| = n, Number of Vertices in a graph
Steps:
- Choose an arbitrary starting vertex s.
- Compute the shortest path from vertex s to v having edge length k, where 0 < k <= |V|.
- Store the computed value in step-2 in an 2-D array say 'dp' ,where dp[k][v] tells shortest length from vertex s to v having edge length k.
- For every vertex v , calculate the Mean Weight using Karp's theorem, max((dp[n][v] - dp[k][v])/(n-k)) where 0<= k <= n-1
- Store the results computed in step-4 in an 1D-array say 'mean'.
- Minimum Mean is the minimum value in the array 'mean'.
How to compute the shortest path?
Dynamic programming can be implemented to find shortest path from vertex s to vertex v containing k edges contains optimal sub-structure and overlapping sub-problems. Recursive Solution
dp[k][v] = min(dp[k][v], dp[k-1][u] + weight(u,v))
For each k in range(0,n), we compute above relation for every vertex v in range(0,n) and store it in dp[k][v]. Here, W(u,v) is a weight of direct edge between vertex u and v.
Implementation
Implementation in C++:
#include<bits/stdc++.h>
using namespace std;
//represents number of edges
int N;
//represents an edge
typedef struct{
int from,weight;
}edge;
vector<edge> edges[N];
void addedge(int from,int to,int weight){
edges[to].push_back({from,weight});
}
//computes the shortest Path
void shortestpath(int dp[][N]){
//intialize all distances to -1
for(int i=0; i<=N; i++){
for(int j=0; j<N; j++)
dp[i][j]= -1;
}
//starting vertex to be first vertex 0
dp[0][0]= 0;
//for all path length
for(int k=1; k<=N; k++){
//for every vertex
for(int v=0; v<N; v++){
//direct edges (u,v)
for(int u=0; u<edges[v].size(); u++){
if(dp[k-1][edges[u].from] == -1)
continue;
int weight_u_to_v=edges[v][u].weight;
if(dp[k][v]==-1)
dp[k][v]= dp[k-1][edges[u].from] + weight_u_to_v;
else
dp[k][v] = min(dp[k][v], dp[k-1][edges[u].from] + weight_u_to_v);
}
}
}
}
//computes minimum mean weight of cycle in graph
double minMeanWeight(){
int dp[N+1][N];
shortestpath(dp);
//stores mean values
double mean[N];
for(int i=0;i<N;i++)
avg[i]=-1;
//Applying Karp's Theorem
for(int i=0;i<N;i++){
if(dp[N][i]==-1)
continue;
for(int k=0;k<N;k++){
if(dp[k][i] != -1)
mean[i] = max(mean[i],((double)dp[N][i]-dp[k][i])/(N-k));
}
}
//computes minimum value from mean[]
double minWeight = mean[0];
for(int i=0;i<N;i++){
if(mean[i] != -1)
minWeight = min(minWeight,mean[i]);
}
//if not found, returns -1
return minWeight;
}
int main(){
N=4;
addedge(0,1,1);
addedge(0,2,10);
addedge(1,2,3);
addedge(2,3,2);
addedge(3,0,8);
addedge(3,1,0);
cout<<minMeanWeight()<<endl;
return 0;
}
Input:
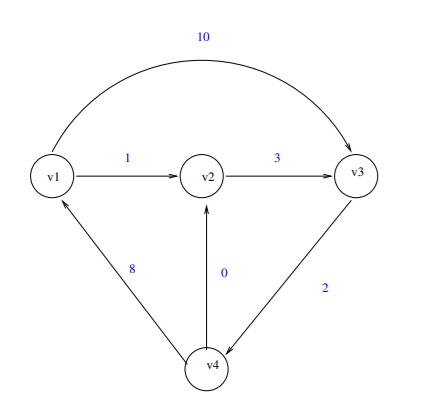
A Table could be generated for following approach, where each entry (i,j) represents a value stored in dp[i][j], 0<=i, j<|V|.
| (k,v) | 0 | 1 | 2 | 3 | 4 | max((dp[n][v] - dp[k][v])/(n-k)) |
|---|---|---|---|---|---|---|
| v1 | 0 | -1 | -1 | 20 | 14 | 7/2 |
| v2 | -1 | 1 | -1 | 12 | 6 | 5/3 |
| v3 | -1 | 10 | 4 | -1 | 15 | 11/2 |
| v4 | -1 | -1 | 12 | 6 | -1 | -1 |
Output:
1.66667
Complexity Analysis
- Time Complexity : O(|V| * |E|), for computation of shortest path using dynamic programming.
- Auxiliary Space Complexity: O(|V| * |E| + |V|), for DP matrix and storing mean weights of every path length
With this article at OpenGenus, you must have a strong idea of Karp's Minimum Mean Cycle Algorithm.
References
- R. M. Karp, A characterization of the minimum cycle mean in a digraph,Discrete mathematics 23 (3) (1978) 309–311
- Introduction to Algorithms - Problem Set 9 Solutions by Massachusetts Institute of Technology courses.csail.mit.edu/6.046/fall01/handouts/ps9sol.pdf
