In this article, we have presented an efficient algorithm to find the maximum area of island in a grid. This includes the concept of BFS and DFS.

Contents

1. Problem Statement
2. Better visual representation of input
3. Brute Force Approach
4. Solving the problem
5. Code
6. Code Walkthrough
7. Output
8. Tracing the code for the example
9. Time and Space Complexity

Problem Statement

We are provided with an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

Example 1:

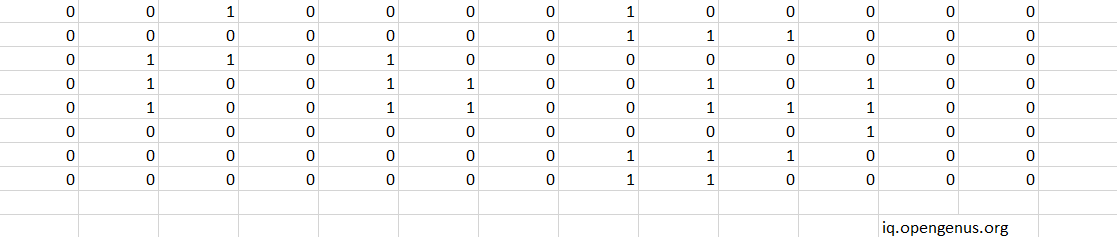
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6

Explanation of Output: The answer is not 11, because the island must be connected 4-directionally.

Example 2:

Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0

Better visual representation of input

For better visual representation of input we are marking the islands with colors.

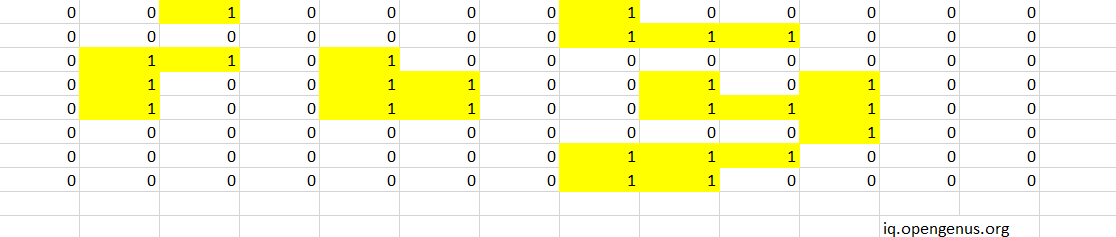
Brute Force Approach

In the brute force approach, we will be checking all possible islands. In this case, we will compute the number of islands in the NxN grid and calculate the area of each island and then, figure out the maximum area.

In a NxN grid, there are O(N³) islands.

For an island of size O(M), the time to calculate the size is O(M). The average size of an island in an NxN grid is O(N²).

This brings the Time Complexity of finding the Maximum Area using brute force approach is O(N⁵).

Solving the problem

Here we have to do 2 things: First get the area of each island

So to find the area of each island or to distinguish an island we use DFS(Depth First Search). Let us see how it works.First we will take an island in the given picture.Suppose we start here.

Its value is 1 .That is it is a part of island.Is the cells surrounding it also 1?If they are we will run DFS on the suuronding cells.This will help us in finding the full island and marking its area.When DfS is run on area which is out of bounds the DFS is gonna return 0.When it sees 0 which denotes water it does nothing.When it sees 1 that is island it recursively runs DFS.But sometimes when we use DFS to reach the surrounding cells sometimes we may reach a cell which is already visited.To avoid this we will use a datastructure visit which is a hashset which mark the positions already visited so we donot end up revisiting them.The DfS of an island should return the area.We will look the cells of the given question if it is 0 we will skip otherwise if it is 1 then we will apply DFS.

Code

The code for the problem in python is:

class Solution:
	def maxAreaOfIsland(self,grid: List[List[int]]) ->int:
        ROWS,COLS = len(grid),len(grid[0])
        visit=set()

	def dfs(r,c):
		if(r<0 or r==ROWS or c<0 or c==COLS or grid[r][c]==0 or (r,c) in visit):
		return 0
		visit.add((r,c))
		return (1+dfs(r+1,c)+dfs(r-1,c)+dfs(r,c+1)+dfs(r,c-1))

	area=0
	for r in range(ROWS):
		for c in range(COLS):
			area = max(area,dfs(r,c))
	return area

Input to the code

we give the grid as input to the code:
grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]

Output

6

Which is the maximum of area among the given islands.

The output area of the island is marked in red in below picture:

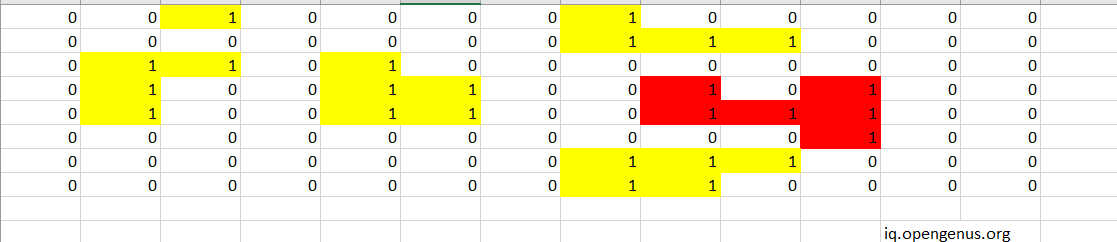
The implementation of the code can be shown visually as:
The first 1 can be represented as a graph below:

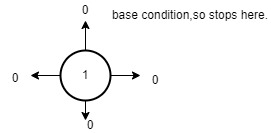
So area =1.

The graph for the next 1 which is present in the 8th column is:

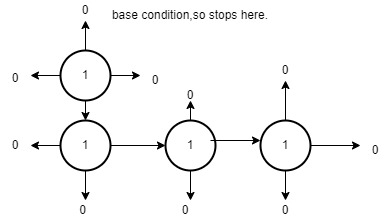
So area is 4.

The graph for the the 1 which is present in the 3rd row 2nd column is:

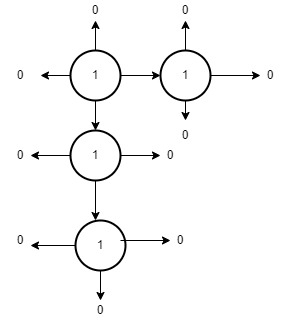
area is 4

The graph for the the 1 at 5th column is:

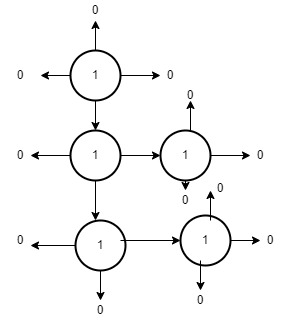
area is 5.

The graph for the the 1 which is present in the 4th row 9th column is:

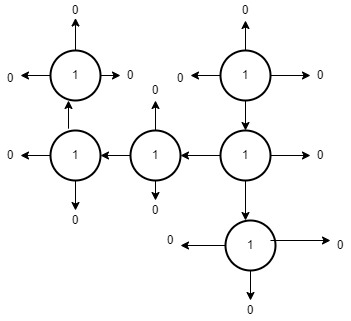
area is 6.

Now the last island that is the graph for the the 1 which is present in the 7th row 8th column is:

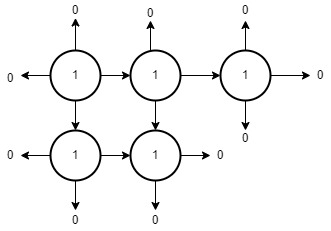
area is 5.

Among these areas 6 is the largest.So we will return 6.

Input2

grid = [[0,0,0,0,0,0,0,0]]

Output2

area: 0

Code Walkthrough

First we will get the number of rows and columns into ROWS and COLS.Next we will declare the visit hashset.Now we will write our recursive root function in which we pass the row r and c column that we are running dfs on.Inside the function we will define the base case as r<0 0r rROWS or c<0 or cCOLS or grid[r][c]==0 ( that is it is water ) or (r,c) in visit (as we do not want to revisit already visited part of an island).In this case we will return 0.

We will add the row column pair (r,c) to visit to indicate that it has been visited by using visit.add.Next we will find the area by adding 1+dfs(r+1,c)+dfs(r-1,c)+dfs(r,c+1)+dfs(r,c-1).1 indicates the area of current cell,dfs(r+1,c) denotes right of the current cell,dfs(r-1,c) denotes left of the current cell,dfs(r,c+1) denotes bottom of the current cell,dfs(r,c-1) denotes top of the current cell.(all 4 directions).Each of these dfs calculates the area of remaining portion of island in the 4 directions.We will return this area.

A variable area is set to 0 .Now we will iterate through the grid using ROWS and COLS in for loop.Every single time we call the dfs function we must update the area variable if the return area is greater than the value in area.This will make sure that we are having the area of the biggest island.Then at last we will return this area.

Tracing the code for the example

Lets take the example given in the question and see how the code will work on it.

In the beginning the first row is scanned the first 2 cells are skipped as they are 0.Then we reach the first cell with 1.

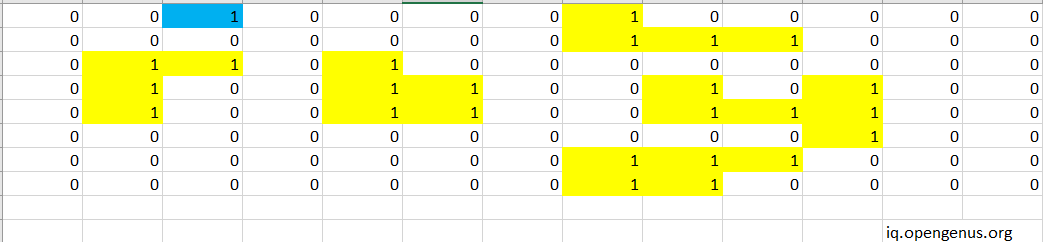
The code will run DFS on the neighbouring cells of this 1 but as they are all 0 it will return the area as 1.Now we will move to the next cells,it will ignore all cells with 0 until it reaches the 8th cell which contains 1.This cell is added to the visit hashset.It will run DFS recursively on its surrounding cells,as above this 1 is unbounded it return 0,its left and right is 0 (that is water) so it returns 0.The cell underneath is 1.This cell is added to the visit hashset and DFS runs recursively on it and marks the 1 to the right of it.This cell is added to the visit hashset.Now DFS runs on this 1 and adds the area of the cell 1 to its right to the area .Now no more recursion possible for that island.So it will return the area as 4.This area is compared with the area variable which is currently 0.So the maximum of these two,that is 4 is taken and the value of area variable is updated as 4.

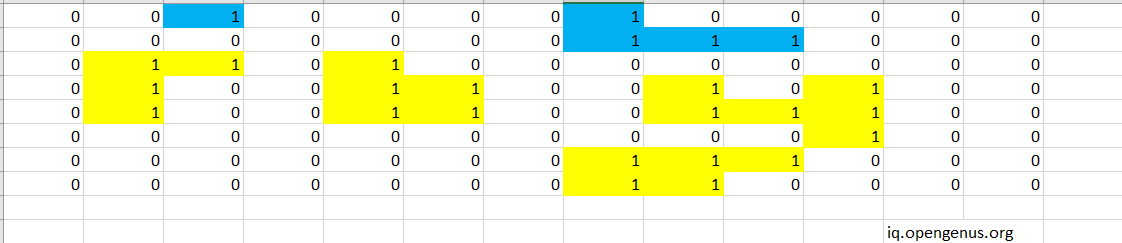
Now we will go for the second row .There is a 1 in the 8th row but it is ignored as it is already present in the visit hashset.Similarly 9th and 10 th cells are also ignored.Now we will go to the 3rd row.The algo ignores the 1st cell as it contains 0. As the next cell is 1 ,it is added to visit,its area added to variable area and DFS is run recursively on itAs the cell under and to the right of it contains 1 they are added to visit and DFS is called recursively on them.The cell under has a cell 1 beneath it,so it is added to visit and DFS runs on it.As no more 1s are present for this island it returns thus marking the area of the island.The area variable has value 4.The returned value is also 4.So the area variable remains as 4.

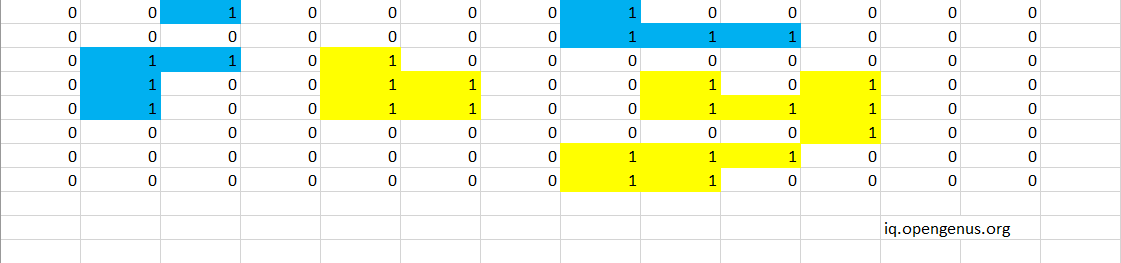
The 3rd cell is ignored as it is already present in visit.Next it reaches the 5 cell which contains 1 as mentioned above runs DFS recursively and returns area as 5.As this returned value is higher than the value present in the area variable which is 4,the value in area is updated as 5.

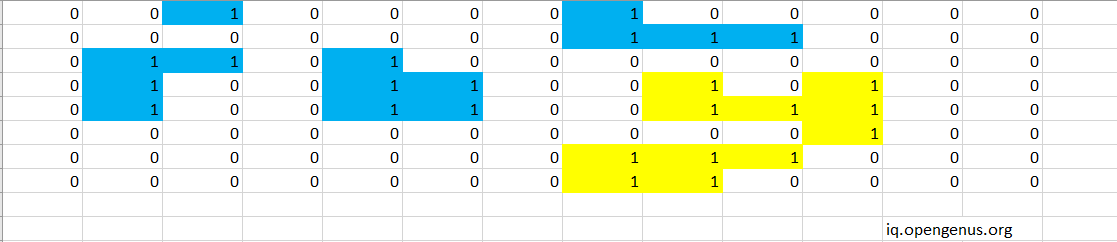
As no more 1 s are present in the 3rd row it will ignore all the rest of the cells in the 3rd row and go to 4 th row.The 1 present in the 2nd,5th and 6th column are ignored as they are already present invisit.Next it reaches the 1 in 9th column and runs DFS recursively on it.It returns the area as 6.This returned value is higher than the value present in the area variable which is 5,the value in area is updated as 6.

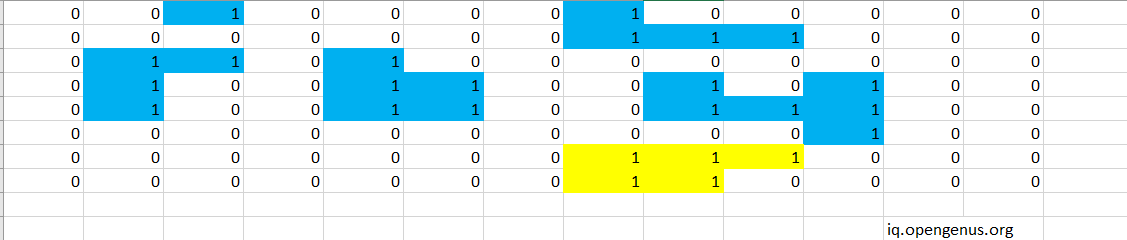
The 1 present in 5th and 6th rows are ignored as they are already present in the visit.In the 7th row,the first 1 is present at 8th colum the algorithm runs recursively on this 1 and its surrounding 1s and returns area as 5.As this returned value is not higher than the value present in the area variable which is 6,the value of variable area remains same.

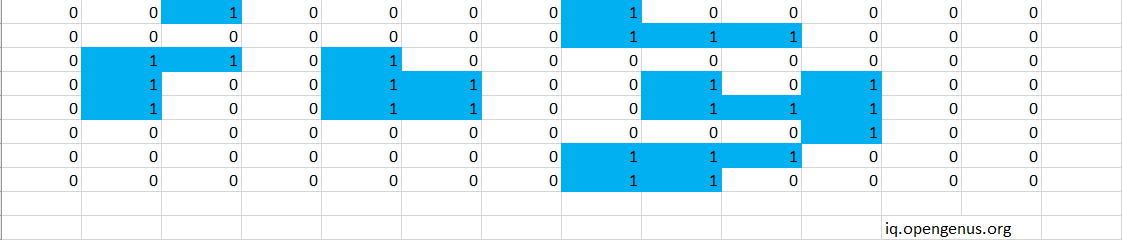
As the 1s in 7th row is already visited it goes to row 8.Here the cells containing 1 are already present in visit.Sow we will ignore it.The algorithm will stop when it reaches the last cell.It returns the value present in the area variable which is 6.We can see that 6 is the maximum among the areas of the islands.

Time and Space Complexity

In worst case we are visiting each cell a constant number of times.So the time complexity is going to be the size of entire grid which is O(M x N) where m is the number of rows and n is the number of columns.For space complexity,we are using a visit hashset which in the worst case can contain every single cell in the grid.Also DFS is recursive so stack is needed to store the return information.So space complexity is O(M x N).

With this article at OpenGenus, you must have the complete idea of how to find the largest island in a grid.