In this article, we have demonstrated the mathematical analysis to find out the minimum number of Comparisons to find the second largest or the second smallest element. We have presented the algorithm for it as well along with other algorithms that look efficient but are not.

In short, the Minimum Comparisons to find Second Largest Element or Second Smallest Element is N + logN - 2 comparisons. Hence, if there are 1024 elements, then we need at least 1024 + 10 - 2 = 1032 comparisons. Also, note that if we need to find the Largest or Smallest element, then we need at least ==1024 comparisons. Hence, there is an increase of 8 comparisons only.

Table of Contents:

1. Problem statement
2. Divide and conquer algorithm
3. Tournament Method
4. Algorithmic approach
5. Complexity Analysis
6. Minimum number of comparisons required
7. Conclusion

Problem statement

The problem is to come up with an algorithmic approach requiring minimum number of comparisons to find the second largest element in an unsorted array.

There can be multiple ways to find the second largest element:

1. In a simple approach we can sort the array in descending order and then return the second element which is not equal to the largest element from the sorted array.
   As sorting the array requires n logn number of comparisons therefore, this approach requires n logn number of comparisons.

2. In another approach we can store two variables and compare all the elements with them so that the variables will only have the values of the two largest elements.
   Since we compare all the elements of the array to these two variables, therefore this approach requires 2n number of comparison.

3. Another approach can be to traverse the array twice. In the first traversal we find the maximum element and in the second traversal, we find the greatest element less than the element obtained in the first traversal.
   This requires 2n-3 comparisons.

Now let us discuss if it is possible to come up with a better approach requiring lesser number of comparisons.

Divide and conquer algorithm

The idea is to present you with an efficient Divide and conquer algorithm to find the second largest element and show you the number of comparisons it requires.

Note: This has the most efficient time complexity possible but it does not make the minimum number of comparisons.

Algorithm:

Let A be the array containing n elements among which we need to find the second largest element.

Step 1: Divide and conquer the array A[0 : n] into two parts, A[0 : n/2 - 1] and A[n/2:n-1]

Step 2: Pair from i=0 to n/2-1. If A[i] > A[i+n/2] then swap A[i] and A[i + n/2]

Step 3: Until the size of the array A[n/2:n-1] is greater than 2, divide and conquer recursively to find the largest value and the second largest value.

If the size of the array A[n/2:n-1] is lesser than or equal to 2, then the largest value and the second largest value are calculated.

Assuming that the largest value is A[p], the second largest value is A[q] then,

Step 4: The largest value is A[p] and the second largest value is the larger of A[p - n/2] and A[q].

Implementation in C++

#include<iostream>
using namespace std;

void secondLargest(int a[],int *largest,int *second,int left,int right)
{
   	int i;
	if(left==right)
	{
		*largest=*second=left;
	}
	else if(left==right-1)
	{
		if(a[left]>a[right])
		{
			*largest=left;
			*second=right;
		}
		else
		{
			*largest=right;
			*second=left;
		}
	}
	else
	{
		int k=(right-left+1)/2;	
		for(i=left; i<left+k; i++)
		{ 
			if(a[i+k] < a[i])
			{
				int temp=a[i];
				a[i]=a[i+k];
				a[i+k]=temp;
			}
		}	
		secondLargest(a,largest,second,left+k,right);
        if(a[*largest-k]>a[*second]) 
			*second=*largest-k;
	}
	
}

Time Complexity: O(n)

Divide and conquere approach does 3n/2 - 2 comparisons.

So, if there are 1000 elements, we need 1498 comparisons to find the second largest element.

Now let us see if there is any better approach that requires lesser number of comparisons.

Tournament Method

The basic idea is to compare the elements in a tournament fashion- we split the elements into pairs, compare each pair and then compare the winners of each pair in the same manner.

We start with finding the largest number in an array. We can find the largest element by comparing the elements as tuples, until only one element remains which is again the largest element in the array.

Now, to find the second largest element,we know that the second largest element wins the comparison battle against all other elements except the largest element. Which means that, the second largest element is already compared with the largest element in one of the step and removed from the comparison tree.The second largest element must be the largest element of the list of loser array which contains all the elements that lost the comparison battle against the largest element and has log₂(n) elements. Thus by finding the largest element of this array using the same approach we get the second largest element.

Now let us discuss how to implement this tournament method to find the second largest element.

Algorithmic approach

We start with finding the largest number in an array. We can find the largest element by comparing the elements as tuples, until only one element remains which is again the largest element in the array.

We can find the second largest element as follows:

1. Find the largest element.
2. Collect all elements of the array that were directly compared to the largest element.
3. Find the largest element among them.

While finding the largest element, we also store all the elements, the largest element was compared to in an array Compared[].Every time any element loses in an comparison to the largest element, we store it in this array. Second largest element is one of the element of this array as it wins over all other elements but loses to the largest element and then find the largest among these elements.

Algorithm:

We design this algorithm in two steps.

Step 1. Here we use FindMaxTournament() to find the largest element in the given array.

FindMaxTournament() algorithm returns an array of integers Compared[0..K] where
• Compared[0] = K (i.e., the 0th element of the array holds the length of the array);
• Compared[1] = max (i.e., the first element of the array is the largest number;
• Compared[2], . . . ,Compared[K] are all numbers with which the largest number has
been compared till now.

Step 2. Here we use FindSecondMax() to find the second largest element in an array, and function FindMaxTournament() is used in it.
First call to the FindMaxTournament() returns the compared array while finding the largest element and the second call to the FindMaxTournament() returns the compared array while finding the second largest element and finally the FindSecondMax() function returns the second largest element.

Algorithm FindSecondMax(N, A[1..N]) returns
begin
    Compared←FindMaxTournament(1,N,A[1..N]);
    Compared2←FindMaxTournament(2,Compared[0],Compared[2..Compared[0]]);
    return Compared2[1]
end

Function FindMaxTournament(I,J, A[I..J],N) returns Compared[0..K]
begin
    if I = J then //base case
        Compared[0..N];
        Compared[0]← 1;
        Compared[1]← A[I];
        return Compared;
    endif
    Compared1← FindMaxTournament(I, I+(J-I)/2, A,N);
    Compared2← FindMaxTournament(1+I+(J-I)/2,J, A,N);
    if Compared1[1]>Compared2[1] then
        K←Compared1[0]+1;
        Compared1[0]←K;
        Compared1[K]←Compared2[1];
        return Compared1;
    else
        K←Compared2[0]+1;
        Compared2[0]←K;
        Compared2[K]←Compared1[1];
        return Compared2;
    endif
end

Complexity Analysis

From the above algorithm, we know that the FindMaxTournament() algorithm, has a running time O(n) for an array of size n, therefore
• The first call to FindMaxTournament() has running time O(n).
• The second call to FindMaxTournament() passes an array of size at most log n and therefore, runs in O(log n).
And hence FindSecondMax() has running time O(n) + O(log(n)) = O(n).

Also an extra compared array of size k is used and as k here is log n ,for n elements, therefore the space complexity is O(log n).

Thus the total time complexity of the algorithm is O(n) and the total space complexity is O(log n).

Minimum number of comparisons required

When we find the largest element by comparing the elements as tuples, until only one element remains which is again the largest element in the array, then

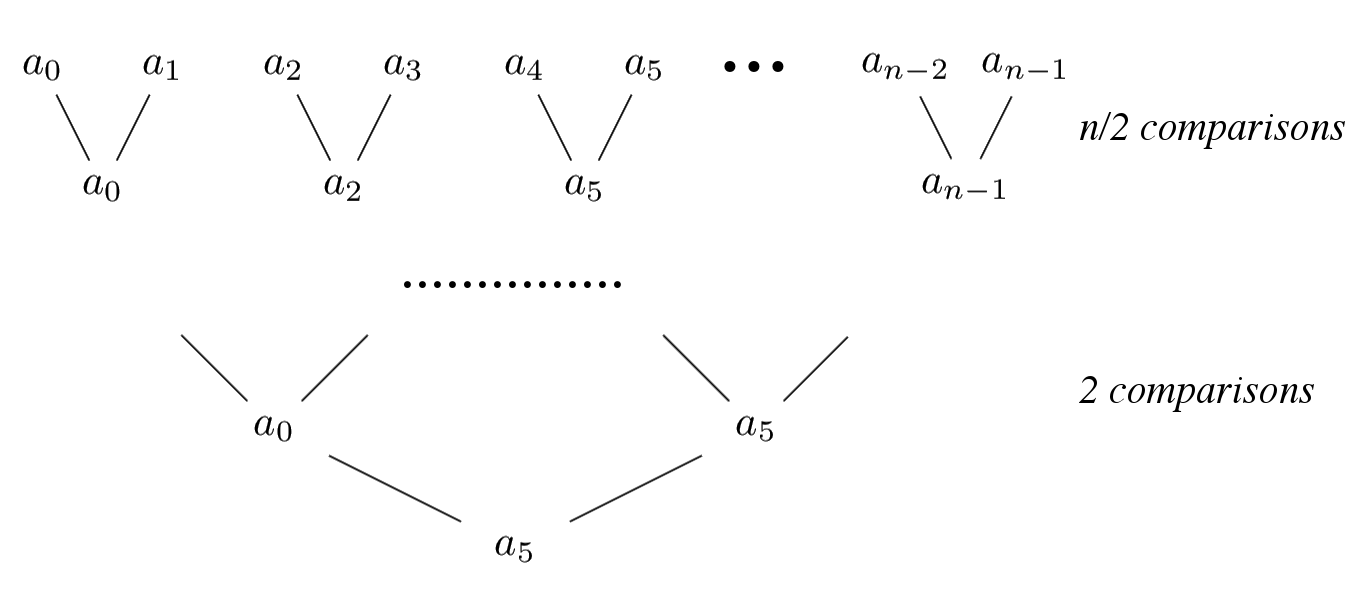
If the number of elements in the array is a power of 2, (n = 2ᵏ) then, to find the largest element, n/2 comparisons must be performed until only one element remains. So, the number of comparisons are

n/2 + n/4 + n/8 + ... + n/(n/2) + n/n = n - 1

So to find the largest element it takes n-1 comparisons. We can also state this from the algorithm that the first call to FindMaxTournament() (to find the largest element) passes an array of size n and hence uses n−1 comparisons.

Also, as discussed earlier, the second largest element wins the comparison battle against all other elements except the largest element and thus the second largest element must be the largest element of the list of losers array which has log n elements. Therefore, the second call to FindMaxTournament() (to find the second largest element) passes an array of size at most log n and therefore, it uses log n − 1 comparisons.

As FindSecondMax() uses n - 1 + log n - 1 comparisons i.e n + log n - 2 comparisons. Therefore to find the second largest element, minimum n + log n - 2 comparisons are required.

Conclusion

The time complexity of both the discussed methods is same i.e O(n) but the second method uses lesser number of comparisons.
Therefore, we conclude that the minimum number of comparisons required to find the second largest element is n + log n - 2.

With this article at OpenGenus, you must have the complete idea of the minimum number of comparisons to find the second largest or the second smallest element.