
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored an insightful approach/ algorithm to find the number of islands in MxN matrix. An extension of this algorithm is used by online battleship game engine.
TABLE OF CONTENTS
- PROBLEM STATEMENT DEFINITION
- PROBLEM ANALYSIS
- SOLUTION ANALYSIS
- METHOD-1 BREADTH-FIRST-SEARCH APPROACH
- Algorithm
- Implementation
- Complexity
- METHOD-2 DEPTH-FIRST-SEARCH WHILE UPDATING MATRIX APPROACH
- Algorithm
- Implementation
- Complexity
- METHOD-3 DEPTH-FIRST-SEARCH WHILE UPDATING MATRIX APPROACH
- Algorithm
- Implementation
- Complexity
- COMPARISON OF APPROACHES
- APPLICATIONS
Prerequisite: Breadth First Search (BFS), Depth First Search (DFS)
Let us get started with Number of Islands in MxN matrix. This is similar to Leetcode problem 200. Number of Islands.
PROBLEM STATEMENT DEFINITION
Given a 2D matrix of 0s and 1s, find total number of clusters or islands formed by elements with value 1 in a sea of 0s.
PROBLEM ANALYSIS
What is an island?
In this particular question an island is a group of connected 1s. Take a look at the image below. Let the green squares represent 1s and the white squares represent 0s. The group of 1s surrounded by the white sea of 0s are an islands. We need to count the number of such clusters.

The program for solving this problem involves getting a 2D matrix of 0s and 1s as input.
For example, let the input be a 10 X 10 matrix:
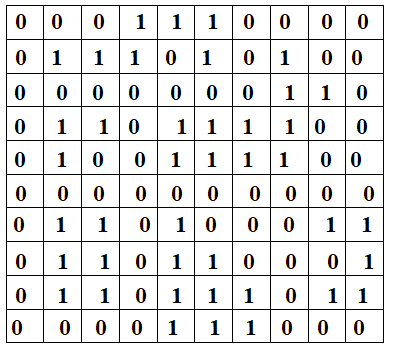
The islands of 1s are:
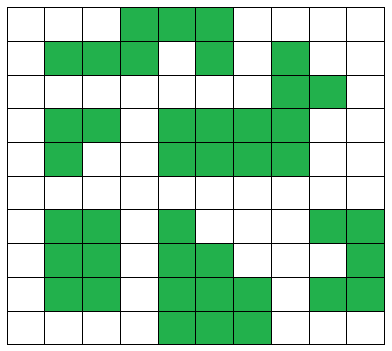
Thus the maximum number of islands are 6
SOLUTION ANALYSIS
The intuitive approach that comes to mind is to search how many different island clusters are present. So, if we start a search from any index with value 1, we can get all the 1s connected to that particular 1. That would constitute our first island group.
So, when we start a search the second time with a different 1, we would be sure to get a different island group. But, it might include the 1s we have already counted as part of the first island group. So, we have to mark the 1s that we have already visited. The other problem with non-memoization is that without keeping track of the 1’s we already visited, we would be stuck in our search loop since we would keep going back on the same 1 again and again.
So, we have two options to keep track of the visited 1s and of course they are:
Using a visited array — We can keep a separate visited array or a hashmap or a set to keep track of visited 1s.
Changing 1s to 0s after visiting them — This method would require no extra space to work and is thus is memory efficient. However this method is not recommended when we have to keep the original array unchanged.
Let us see three approaches using not-so-efficient BFS, DFS and non-memoized DFS.
METHOD-1) BREADTH-FIRST-SEARCH APPROACH
The approach is the same as described above expect we use BFS instead of DFS. We make our computation easier by including a visited array.
While considering the matrix as a graph, the following points must be kept in mind:
- An element matrix[i][j] with value 1 is considered as a vertex.
- All adjacent elements of matrix[i][j] with value 1 are considered as its neighbor vertices.
- An element can have maximum of eight neighbors.
Algorithm
- Initialize count to 0.
- Initialize a 2D 'visited' array of booleans which is of size equal to given matrix. Initialize all elements of 'visited' array to false.
- Repeat the following steps for all the elements of given 2D matrix.
- For an element matrix[i][j], if matrix[i][j] is 1 and visited[i][j] is 'false' then
- Increment count by 1.
- Start breadth first search from element matrix[i][j].
- Mark all the neighboring 1s as visited
- Return count
code
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) return 0;
int islands = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == '1') {
islands++;
BFS(grid, i, j);
}
}
}
return islands;
}
private void BFS(char[][] grid, int x, int y) {
// Mark the land as visited by setting it to '0'
grid[x][y] = '0';
Queue<int[]> q = new LinkedList<int[]>();
q.offer(new int[]{x, y});
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; // input values
while (q.size() > 0) {
int size = q.size();
int[] p = q.poll();
for (int i = 0; i < size; i++) {
for (int[] dir : dirs) {
int x1 = p[0] + dir[0];
int y1 = p[1] + dir[1];
// Invalid neighbor skipped
if(x1 < 0 || x1 >= grid.length || y1 < 0 || y1 >= grid[0].length)
continue;
if (grid[x1][y1] == '1') {
grid[x1][y1] = '0';
q.offer(new int[] {x1, y1});
}
}
}
}
}
C++ Implementation
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
int row[] = { -1, -1, -1, 0, 1, 0, 1, 1 };
int col[] = { -1, 1, 0, -1, -1, 1, 0, 1 };
bool isSafe(vector<vector<int>> const &mat, int x, int y, vector<vector<bool>> const &processed)
{
return (x >= 0 && x < mat.size()) && (y >= 0 && y < mat[0].size()) && mat[x][y] && !processed[x][y];
}
void BFS(vector<vector<int>> const &mat, vector<vector<bool>> &processed, int i, int j)
{
queue<pair<int, int>> q;
q.push(make_pair(i, j));
processed[i][j] = true;
while (!q.empty())
{
int x = q.front().first;
int y = q.front().second;
q.pop();
for (int k = 0; k < 8; k++)
{
if (isSafe(mat, x + row[k], y + col[k], processed))
{
processed[x + row[k]][y + col[k]] = 1;
q.push(make_pair(x + row[k], y + col[k]));
}
}
}
}
int countIslands(vector<vector<int>> const &mat)
{
if (mat.size() == 0) {
return 0;
}
int M = mat.size();
int N = mat[0].size();
vector<vector<bool>> processed(M, vector<bool>(N));
int island = 0;
for (int i = 0; i < M; i++)
{
for (int j = 0; j < N; j++)
{
if (mat[i][j] && processed[i][j] == 0)
{
BFS(mat, processed, i, j);
island++;
}
}
}
return island;
}
int main()
{
vector<vector<int>> mat =
{
{ 1, 0, 1, 0, 0, 0, 1, 1, 1, 1 },
{ 0, 0, 1, 0, 1, 0, 1, 0, 0, 0 },
{ 1, 1, 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 0, 1, 0, 0, 0, 0 },
{ 1, 1, 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 0, 1, 0, 0, 1, 1, 1, 1 },
{ 0, 0, 0, 0, 0, 1, 1, 1, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 1, 1, 1, 0 },
{ 1, 0, 1, 0, 1, 0, 0, 1, 0, 0 },
{ 1, 1, 1, 1, 0, 0, 0, 1, 1, 1 }
};
cout << "The maximum number of islands is: " << countIslands(mat) << endl;
return 0;
}
Output
The maximum number of islands is: 3
Time Complexity
We need to traverse across the entire matrix and perform the inefficient BFS. If the number of rows are n and the numbers of columns are n then the time complexity is:
- Worst case time complexity:
Θ(n^3) - Average case time complexity:
Θ(n^2 * g)(if the number of 1s is g) - Best case time complexity:
Θ(n * m)(n is the number of rows and m is the number of columns and there are no 1s)
Space Complexity
We make use of an array to store all visited 1s. Hence the Space complexity is Θ(n^2)
METHOD-2) DEPTH-FIRST-SEARCH WHILE UPDATING MATRIX APPROACH
In this approach we modify the DFS function to first check whether we are in the bounds of the matrix. If not, return. Also, if we have a 0 in the current position, we return. We then convert the 1 in the current position to a 0. Finally, we perform DFS on all eight adjacent positions (top, bottom, left, right, top-left, top-right, bottom-left, bottom-right).
Algorithm
- Read the input binary valued matrix
- Initialize count = 0
- Traverse every element
- If matrix[i][j] is 1, then make it to 0 and increment count while performing the following 2 steps.
- Perform DFS on the 8 surrounding elements of the current element.
- When we reach 0 from all sides break from the DFS function and move to the next element in the matrix (ie matrix[i][j+1])
- Return count
Code
#include <bits/stdc++.h>
using namespace std;
void DFS(vector<vector<int>> &M, int i, int j, int n, int m)
{
if (i < 0 || j < 0 || i > (n - 1) || j > (m - 1) || M[i][j] != 1)
{
return;
}
if (M[i][j] == 1)
{
M[i][j] = 0;
DFS(M, i + 1, j, n, m);
DFS(M, i - 1, j, n, m);
DFS(M, i, j + 1, n, m);
DFS(M, i, j - 1, n, m);
DFS(M, i + 1, j + 1, n, m);
DFS(M, i - 1, j - 1, n, m);
DFS(M, i + 1, j - 1, n, m);
DFS(M, i - 1, j + 1, n, m);
}
}
int countIslands(vector<vector<int>> &M)
{
int n = M.size();
int m = M[0].size();
int count = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (M[i][j] == 1)
{
M[i][j] = 0;
count++;
DFS(M, i + 1, j, n, m);
DFS(M, i - 1, j, n, m);
DFS(M, i, j + 1, n, m);
DFS(M, i, j - 1, n, m);
DFS(M, i + 1, j + 1, n, m);
DFS(M, i - 1, j - 1, n, m);
DFS(M, i + 1, j - 1, n, m);
DFS(M, i - 1, j + 1, n, m);
}
}
}
return count;
}
int main()
{
vector<vector<int>> M = {{1, 1, 0, 1, 1},
{1, 1, 0, 1, 1},
{1, 0, 0, 1, 1},
{0, 0, 0, 0, 0},
{1, 1, 1, 1, 1}};
cout << "The maximum number of islands is: " << countIslands(M);
return 0;
}
Output
The maximum number of islands is: 3
Time Complexity
We need to perform DFS for every element in the matrix at least once. If the number of rows are n and the numbers of columns are n then the time complexity is:
- Worst case time complexity:
Θ(n * m) - Average case time complexity:
Θ(n * m) - Best case time complexity:
Θ(n * m)
where, n is the number of rows and m is the number of columns
Space Complexity
We do not use any additional space. Hence the Space complexity is Θ(n * m) (n is the number of rows and m is the number of columns)
METHOD-3) DEPTH-FIRST-SEARCH WITH VISITED ARRAY APPROACH
In this approach we modify the DFS function to first check whether we are in the bounds of the matrix .If not, return. Also, if we are currently pointing to an element in the visited array, we return. We then add the non-visited elements to the visited array. Finally, perform DFS for the next unvisited element.
Algorithm
- Read the input binary valued matrix
- Initialize count = 0
- Traverse every element
- If matrix[i][j] is 1, Check if it is visited.
- If not then add this element to visited array and increment count.
- Perform DFS on the 8 surrounding elements of the current element.
- When we reach 0 from all sides break from the DFS function and move to the next element in the matrix (ie matrix[i][j+1])
- Return count
Code
#include <bits/stdc++.h>
using namespace std;
#define ROW 5
#define COL 5
int isSafe(int M[][COL], int row, int col, bool visited[][COL]);
void DFS(int M[][COL], int row, int col, bool visited[][COL]);
int countIslands(int M[][COL]);
int main()
{
int M[][COL] = { { 1, 1, 0, 0, 0 },
{ 0, 1, 0, 0, 1 },
{ 1, 0, 0, 1, 1 },
{ 0, 0, 0, 0, 0 },
{ 1, 0, 1, 0, 1 } };
cout << "The maximum number of islands is: " << countIslands(M);
return 0;
}
int isSafe(int M[][COL], int row, int col, bool visited[][COL])
{
return (row >= 0) && (row < ROW) && (col >= 0) && (col < COL) && (M[row][col] && !visited[row][col]);
}
void DFS(int M[][COL], int row, int col, bool visited[][COL])
{
// The following two rows are used to find the 8 surrounding elements of the elements under consideration
int rowNbr[] = { -1, -1, -1, 0, 0, 1, 1, 1 };
int colNbr[] = { -1, 0, 1, -1, 1, -1, 0, 1 };
visited[row][col] = true; for (int k = 0; k < 8; ++k)
if (isSafe(M, row + rowNbr[k], col + colNbr[k], visited))
DFS(M, row + rowNbr[k], col + colNbr[k], visited);
}
int countIslands(int M[][COL])
{
bool visited[ROW][COL];
memset(visited, 0, sizeof(visited));
int count = 0;
for (int i = 0; i < ROW; ++i)
for (int j = 0; j < COL; ++j)
if (M[i][j] && !visited[i][j]) {
DFS(M, i, j, visited);
++count;
}
return count;
}
Output
The maximum number of islands is: 5
Time Complexity
The time complexity depends on the layout, but at the worst case we are looking up the 1s in each of the disjoint groups, so O(n^2) for n rows and n columns.
- Worst case time complexity:
Θ(n * m)(n is the number of rows and m is the number of columns) - Average case time complexity:
Θ(n * m)(n is the number of rows and m is the number of columns) - Best case time complexity:
Θ(n * m)(n is the number of rows and m is the number of columns)
Space Complexity
The space complexity is proportional to the number of 1s in the matrix, but at the worst case we have to store n * m 1s . Hence the Space complexity is Θ(n * m) (n is the number of rows and m is the number of columns)
COMPARISON OF APPROACHES
| Complexity | Method-1 | Method-2 | Method-2 |
|---|---|---|---|
| Time-Complexity | n^3 (worst-case) | n * m | n * m |
| Space-Complexity | 1 | n * m | n * m |
APPLICATIONS
- An extension of this algorithm is used by online battleship game engines.
- It is used used in other computational geometry problems.
- An extension of this algorithm is used by photo editing softwares to find common color scales of the image. It considers the colour scale to be found as 1 and all others as 0.
Question
What is the best approach is the best to solve this problem?
With this article at OpenGenus, you must have the complete idea of solving "Number of Islands in MxN matrix (of 0 and 1)".
