Breadth first search (BFS) is one of the most used graph traversal techniques where nodes at the same level are traversed first before going into the next level. Queue is used internally in its implementation.

In graph theory the most important process is the graph traversal.In this we have to make sure that we traverse each and every node of the graph.Now there are mainly two methods of traversals:

1. BFS: breadth first search
2. DFS: depth first search

In this article we are going to discuss about breadth first search (BFS).

The way to look:

The BFS looks like we are exploring the graph layer-wise.

In this we start from a source node and then we travel to other nodes based on their adjacent nodes.In other words we explore the graph more like breadth wise.

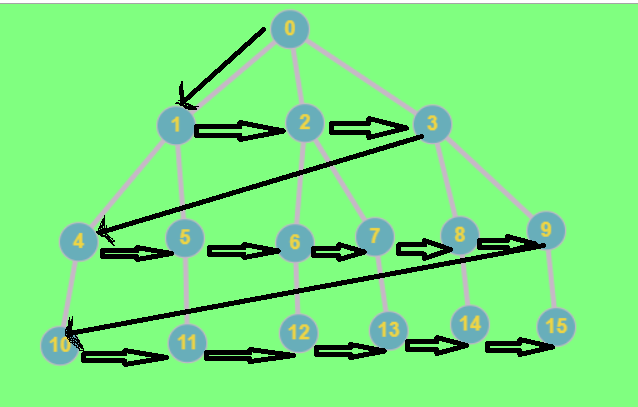
as we can see in the above image we see layers of the graph being traversed.This is what BFS is.

Now while processing nodes we might end up processing the same node again and again.
So we make sure we mark the visited arrays.We do this with help of a boolean array.Once we visit a node, we store the same in the same order of visit, this is done so that we visit the children of the nodes in the same order of the layer.
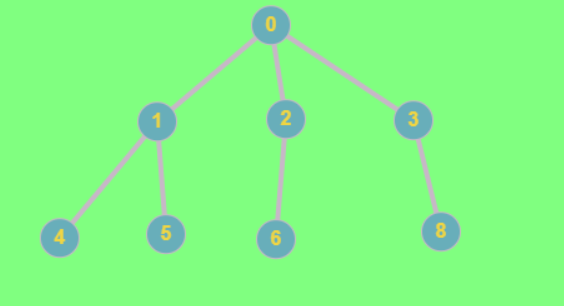
Let's look at the above example to understand this in more detail.

in the above graph, we traverse through the nodes of 0, then we go to 1, 2 and 3.we store these nodes in the same order of visit, so that we can visit the children of 1(i.e. 4,5) first and then 2(i.e. 6.7) and 3(i.e.8,9).

The Queue:

This processing/storing work is done by a Queue.The queue follows the First In First Out (FIFO) queuing method, and therefore, the neighbors of the node will be visited in the order in which they were inserted in the node i.e. the node that was inserted first will be visited first, and so on.

The algorithm:

BFS (G, s)                   
      Q.enqueue( s ) //add the source node to the queue first

      tag s as visited
      while ( Q is not empty)
          
           v  =  Q.dequeue( )

          for all neighbours w of v in Graph G
               if w is not visited 
                        Q.enqueue( w )             
                        tag w as visited

now lets try and apply this algorithm on a specific example:

here lets assume the source node is '0'.
before the loop starts s is enqueued.

first iteration:
s is popped from the queue.
The neighbors of 0 , i.e. 1,2,3 are enqueued and marked as "visited".

second iteration:

1 is popped, the neighbors of 1 , i.e. 4,5 are pushed and marked "visited".

third iteration:

2 is popped, the neighbor of 2 , i.e. 5 is pushed and marked "visited".

fourth iteration:

3 is popped, the neighbor of 3 , i.e. 8 is pushed and marked "visited".

fifth iteration:

4 is popped, the neighbor of 4 , i.e. 1 is marked already "visited" so it is ignored.

sixth iteration:

5 is popped, the neighbor of 5 , i.e. 1 is marked already "visited" so it is ignored.

seventh iteration:

6 is popped, the neighbor of 6 , i.e. 2 is marked already "visited" so it is ignored.

eighth iteration:

8 is popped, the neighbor of 8 , i.e. 3 is marked already "visited" so it is ignored.

The queue becomes empty, so algorithm stops.

Code

#include<iostream.h>
#include<conio.h>
#include<stdlib.h>
int cost[10][10];
int i,j,k,n,qu[10],front,rare,v,visit[10],visited[10];
int main()
{
    int m;
    clrscr();
    cout <<"Enter no of vertices:";
    cin >> n;
    cout <<"Enter no of edges:";
    cin >> m;
    cout <<"\nEDGES \n";
    for(k=1; k<=m; k++)
    {
        cin >>i>>j;
        cost[i][j]=1;
    }
    cout <<"Enter initial vertex to traverse from:";
    cin >>v;
    cout <<"Visitied vertices:";
    cout <<v<<" ";
    visited[v]=1;
    k=1;
    while(k<n)
    {
        for(j=1; j<=n; j++)
            if(cost[v][j]!=0 && visited[j]!=1 && visit[j]!=1)
            {
                visit[j]=1;
                qu[rare++]=j;
            }
        v=qu[front++];
        cout<<v <<" ";
        k++;
        visit[v]=0;
        visited[v]=1;
    }
    getch();
    return 0;

output:

Enter no of vertices:4
Enter no of edges:4
EDGES
1 2
1 3
2 4
3 4
Enter initial vertex to traverse from:1
Visited vertices:1 2 3 4
12

Time complexity

The time complexity of BFS is O(V + E).
V=vertices
E= edges

Applications of BFS

BFS is in fact used in a lot of places:

1.BFS is very versatile, we can find the shortest path and longest path in an undirected and unweighted graph using BFS only.

Well in case of shortest path we just do a small modification and store the node that precedes. So that after each step we can choose the smallest path, hence following the minimum possible path all the time , we end up choosing the total minimum path.

Now in case of the longest path we use the double BFS method. So we first BFS from any one node, and then start another from the one we end up, so we get the longest path of the graph.

2.BFS is widely used in MAPS and GPS driven technologies.

3.A platform that requires peer to peer network is bound to use BFS somewhere or the other.

4.Cycle detection in an undirected/directed graph can be done by BFS.

5.If we want to check if two nodes have a path existing between them then we can use BFS.

6.All algorithms like Djkstra and Bellman-ford are extensive use of BFS only.

BFS vs DFS

• BFS: This algorithm as the name suggests prefers to scan breadth/layer wise.
• DFS: This algorithm as the name suggests prefers to scan Depth wise
• BFS: uses queue as the storing data structure.
• DFS: uses stack as the storing data structure.
• BFS: for any traversal BFS uses minimum number of steps to reach te destination.
• DFS: while in DFS it can travel through unnecessary steps.

while in case of time complexity both have the same as O(v+e)
where v:vertex E: edges

This is all about the basics of BFS at OpenGenus. Happy coing.