Contents

1.Introduction
2.Preorder Traversal of a Tree
3.Methods to find Preorder Traversal of a Tree
4.Iterative Approach
1.Code
2.Output
3.Time Complexity of the Approach
4.Space Complexity of the Approach
5.Recursive Approach
1.Code
2.Output
3.Time Complexity of the Approach
4.Space Complexity of the Approach

Introduction

Preorder traversal is one of the traversal in binary tree in which the root node is visited first then the left subtree and then the right subtree.The order can be written as ROOT LEFT RIGHT.

Preorder Traversal of a Tree

Let us see the pre order traversal of a tree to understand the concept:

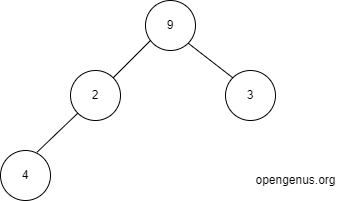
First the root is visited and it is printed.So 9 is printed.So we get
9
Then the left subtree of 9 is visited that is 2.Now 2 is the root.it is printed.So we get
9 2
The left subtree of 2 is visited that is 4.Now 4 is the root.it is printed.So we get
9 2 4
The left subtree of 4 is visited which is Null as no element is present at left of 4.So we visit right of 4 ,which is also Null.So we will go back to 2.The left of 2 is already visited so now right of 2 is visited which is Null.So we will go back to 9 and visit its right subtree which is 3.Now 3 is the root.it is printed.So we get
9 2 4 3.
The left subtree of 3 is visited which is Null as no element is present at left of 3.So we visit right of 3 ,which is also Null.So we will stop the process as all the nodes are visited.So the final preorder traversal of the binary tree will give:
9 2 4 3.

Methods to find Preorder Traversal of a Tree

We can find the Preorder Traversal of a Tree in 2 methods:

1. The iterative approach
2. Recursive Approach
   Let's see the 2 approaches in detail.

Iterative Approach

In the iterative approach we will make use of a stack.Let us find the preorder traversal of graph below:

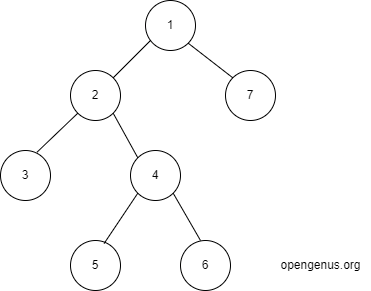
In this tree first we visit 1.Then the left of it which is 2 is visited.Now we visit 3 which is the left of 2.No element in left and right of 3.So we will visit right of 2 which is 4.Now we visit 5 which is the left of 4.No element in left and right of 5.So we will visit right of 4 which is 6.No element in left and right of 6.So we will visit right of 1 which is 7.No more node to be processed.So we will get the preorder traversal as:
1 2 3 4 5 6 7
Now we will make use of stack.Push the root into the stack.

We will pop whatever is top of the stack and print it.So 1 is popped and printed.The output will be:
1
The stack is empty.Now first take the right then take the left of 1 and push it into the stack.So we will push 7 and then 2.

Now pop whatever is top of the stack and print it.So 2 is popped and printed.The output will be:
1 2
Now first take the right then take the left of 2 and push it into the stack.So we will push 4 and then 3.The stack will look like:

Pop whatever is top of the stack and print it.So 3 is popped and printed.The output will be:
1 2 3
We have nothing on left and right of 3.So we will print 4 and push the right of 4 and then the left of 3.Output is:
1 2 3 4
Stack is:

We will pop 5 which is on top of stack and print it.
1 2 3 4 5 .We have nothing on left and right of 5.So we will print 6
1 2 3 4 5 6
nothing on left and right of 6.So we will print 7.
1 2 3 4 5 6 7.Nothing on left and right of 7.Now the stack becomes empty.So the entire preorder traversal is done.
The final preorder traversal will be:1 2 3 4 5 6 7.

Code

The code for the above steps in java is:

import java.util.*;

class Node {
    int data;
    Node left, right;
    Node(int data) {
        this.data = data;
        left = right = null;
    }
}
public class TUF {
    static ArrayList < Integer > preOrderTrav(Node curr) {
        ArrayList < Integer > preOrder = new ArrayList < Integer > ();
        if (curr == null)
            return preOrder;

        Stack < Node > s = new Stack < > ();
        s.push(curr);

        while (!s.isEmpty()) {
            Node topNode = s.peek();
            preOrder.add(topNode.data);
            s.pop();
            if (topNode.right != null)
                s.push(topNode.right);
            if (topNode.left != null)
                s.push(topNode.left);
        }
        return preOrder;

    }


    public static void main(String args[]) {


        Node root = new Node(11);
        root.left = new Node(90);
        root.right = new Node(89);
        root.left.left = new Node(44);
        root.left.right = new Node(65);
        root.left.right.left = new Node(18);
        root.right.left = new Node(62);
        root.right.right = new Node(37);
        root.right.right.left = new Node(79);
        root.right.right.right = new Node(110);




        ArrayList < Integer > preOrder = new ArrayList < > ();
        preOrder = preOrderTrav(root);

        System.out.print( "PreOrder Traversal of the given tree is : ");
        for (int i = 0; i < preOrder.size(); i++) {
            System.out.print(preOrder.get(i) + " ");
        }

    }
}

Output

PreOrder Traversal of the given tree is : 
11 90 44 65 18 89 62 37 79 110.

Time Complexity of the Approach

As we are visiting all the nodes ,the time complexity will be same as the number of nodes.Let n be the number of nodes.Then the time complexity will be: O(n).

Space Complexity of the Approach

We have to store all the nodes in the worst case so the time complexity will be O(n) where n is the number of nodes.

Recursive Approach

In the recursive approach we will call the preOrder function recursively.If the tree has no nodes it will return nothing.Otherwise it will print the data of the node for which it s called as it considers it as new root and then recursively calls itself by passing the left child of it and right child of it as parameters respectively.Let us first see the code and then the implementation

Code

The function preorder can be written as:

public void preOrder(TreeNode root) {
		if(root == null) {
			return;
		}

		System.out.print(root.data + " ");
		preOrder(root.left);
		preOrder(root.right);
	}

Now we will see the demonstartion of this code in the graph given below:

As this is a recursive function call we can define a stack to store the instances

First we will call preOrder function by passing the root that is 9 as parameter.As 9 is not null so it will print 9.Then it will recursively call preOrder function for the left child of 9 which is 2.So the parameters of the preOrder function for 9 will be pushed to the stack.The stack will look like:

output: 9
As 2 is not null so it will print 2.Then it will recursively call preOrder function for the left child of 2 which is 4.So the parameters of the preOrder function for 2 will be pushed to the stack.The stack will look like:

output: 9 2
4 is not null so it will print 4.Then it will recursively call preOrder function for the left child of 4 which is null.So the parameters of the preOrder function for 4 will be pushed to the stack.The stack will look like:

output: 9 2 4
Null will be pushed to the stack.

As it is null it will return.So null will be removed from call stack and will continue to execute the preOrder method present on top of stack.So now we will call preOrder for right of 4 which is null.So it will return.Now the method for 4 is executed so it will be popped from the call stack.

Now we will call preOrder for right of 2 which is null.So it will return.Now the method for 2 is executed so it will be popped from the call stack.

The execution point will reach to the point 9.Now we will preOrder for right of 9 which is 3.So the parameters of the preOrder function for 3 will be pushed to the stack.The stack will look like:

As 3 is not null so it will print 3.Then it will recursively call preOrder function for the left child of 3 which is null.So it will return.preOrder function will be called for the right child of 3 which is null.So it will return.Now the method for 3 is executed so it will be popped from the call stack.

output: 9 2 4 3
The method for 9 is executed so it will be popped from the call stack.So now the stack will become empty.So we have obtained the preorder traversal as:9 2 4 3.

Time Complexity of the Approach

We have to visit all the nodes.So the time complexity will be O(n) where n=number of nodes.

Space Complexity of the Approach

We are making use of a stack in the recursive calls.So in worst case the size occupied can be the number of nodes.Therefore the space complexity will be O(n).

Hurray! We have finished preorder traversal of a binary tree.