
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Push relabel algorithm is also known as Preflow Push algorithm. It is used for computing maximum flows in a flow network.
Maximum flow in a network graph
In a network graph where every edge has a given capacity, maximum flow is defined as the maximum amount of flow that can move from source to sink. Maximum flow is calculated keeping in mind two constraints,
- For every vertex (except source and sink), incoming flow is equal to outgoing flow.
- Flow of an edge shouldn't exceed its capacity.
Conceptual framework
The idea behind the algorithm is that the edges act as pipes and vertices act as joints and the water flows from a high height to a low hight. Every node is assigned a height variable. The source is considered to be at the highest height |V| and sink is at the lowest height 0.
Push operation
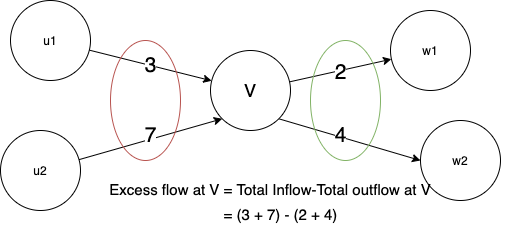
Every vertex is also assigned another variable excess flow. When a vertex has an excess flow, it pushes it to a lower height vertex. The amount of flow pushed is equal to the minimum of excess flow of vertex and capacity of connecting edge.
Excess flow at a vertex V is defined by: Total flow received by V - Total flow going out of V.
Relabel operation
If the height of a vertex is low and the water is overflowing in that vertex, i.e the water gets locally trapped, then it's relabled. In a relabel operation, the height of the vertex is increased.
Pseudocode
We initialise the graph with height of source vertex as V. The height and excess flow of all the other vertices as 0. We keep of performing push and relabel till the excess flow at all the vertices (except source and sink) is zero.
Initialise height of all the vertices as 0
Initialise Height of source = V
Initialise excess flow of all the vertices as 0
For all neighbouring vertices of source node:
Flow and excess flow = capacity of the connecting source-neighbour edge
While there is a vertex with excess flow:
Perform push or relabel
At the end all the vertices should have 0 excess flow
Return maximum flow
Code
import java.util.*;
class Vertex{
int h;
int excess_flow;
Vertex(){
h=0;
excess_flow=0;
}
}
class Graph{
int v;
int e;
Vertex[] vertices;
int[][] capacity;
int[][] flow;
Graph(int v,int e ){
this.v=v;
this.e=e;
vertices=new Vertex[v];
for(int i=0;i<v;i++){
vertices[i]=new Vertex();
}
capacity=new int[v][v];
flow=new int[v][v];
for(int i=0;i<v;i++){
for(int j=0;j<v;j++){
flow[i][j]=0;
}
}
}
void AddEdge(int x,int y, int cap){
capacity[x][y]=cap;
}
int getOverflowVertex(int s,int t){
for(int i=1;i<v-1;i++){
if(vertices[i].excess_flow>0)
{
for(int j=0;j<v;j++){
if(capacity[i][j]!=0){
if(capacity[i][j]!=flow[i][j]){
return i;
}
}
}
}
}
return -1;
}
public void preflow(int s){
vertices[s].h=v;
for(int i=1;i<v;i++){
if(capacity[s][i]!=0){
flow[s][i]=capacity[s][i];
vertices[i].excess_flow+=flow[s][i];
AddEdge(i, s, 0);
flow[i][s]=-flow[s][i];
}
}
}
boolean push(int u){
for(int i=0;i<v;i++){
if(capacity[u][i]!=0){
if(flow[u][i]==capacity[u][i])
continue;
if(vertices[u].h>vertices[i].h){
int Flow=Math.min(capacity[u][i]-flow[u][i],vertices[u].excess_flow );
vertices[u].excess_flow-=Flow;
vertices[i].excess_flow+=Flow;
flow[u][i]+=Flow;
flow[i][u]-=Flow;
return true;
}
}
}
return false;
}
void relabel(int u){
System.out.println(u+"preflow");
int minh=Integer.MAX_VALUE;
for(int i=0;i<v;i++){
if(capacity[u][i]!=0){
if(capacity[u][i]==flow[u][i])
continue;
if(vertices[i].h<minh){
minh=vertices[i].h;
vertices[u].h=minh+1;
}
}
}
}
int maxFlow(int s,int t){
preflow(s);
int u=getOverflowVertex(s,t);
while(u!=-1){
if(!push(u))
relabel(u);
u=getOverflowVertex(s,t);
}
return vertices[t].excess_flow;
}
}
class pushrelabel{
public static void main(String[] args) {
Scanner s=new Scanner(System.in);
System.out.println("Enter no. of vertices");
int v=s.nextInt();
System.out.println("Enter no. of edges");
int e=s.nextInt();
Graph G=new Graph(v,e);
System.out.println("Enter edges and their capacity");
for(int i=0;i<e;i++){
int x=s.nextInt();
int y=s.nextInt();
int cap=s.nextInt();
G.AddEdge(x, y, cap);
}
System.out.println("Enter source and sink");
int S=s.nextInt();
int T=s.nextInt();
System.out.println("The max flow is : "+G.maxFlow(S,T));
}
}
Time complexity
Push relabel algorithm calculates maximum flow in O(V2E) time where V is the number of vertices and E is the number of edges in the network. It is more efficient that Ford Fulkerson's algorithm
Example
Let's understand the working of Push Relabel algorithm from a working example
- Take the following graph
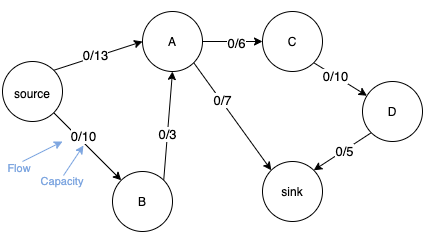
- Initialise the graph by setting heights and excess flow
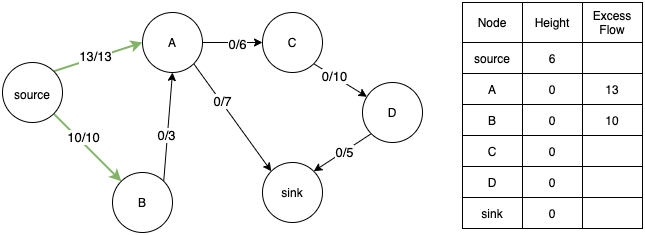
- Consider vertex B. It cannot transfer its excess flow as its adjacent node A has the same height. So we relabel it.
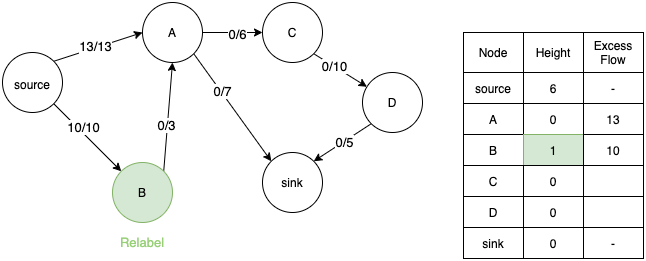
- Now B can push its excess flow to A
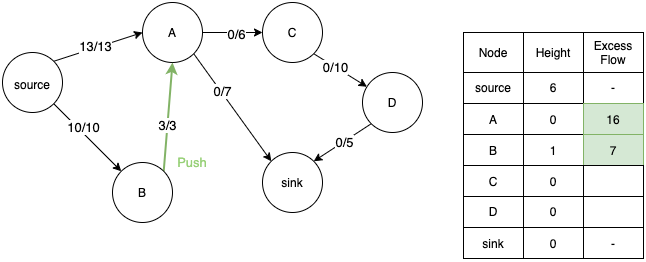
- Similarly consider node A. We relabel its height to 1 so that it can transfer flow to its adjacent nodes C and sink.
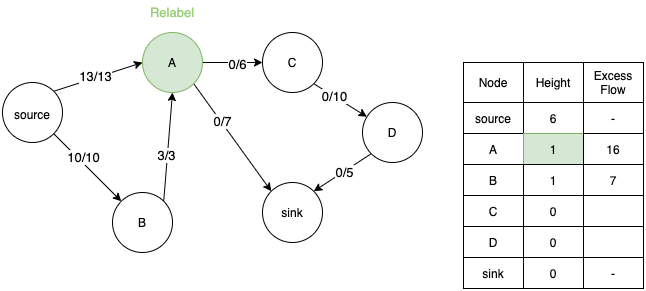
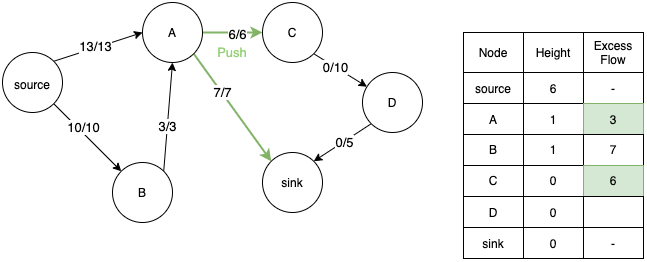
- Now we consider node C and relabel its height, but now flow cannot travel from A to C since they are at the same height.
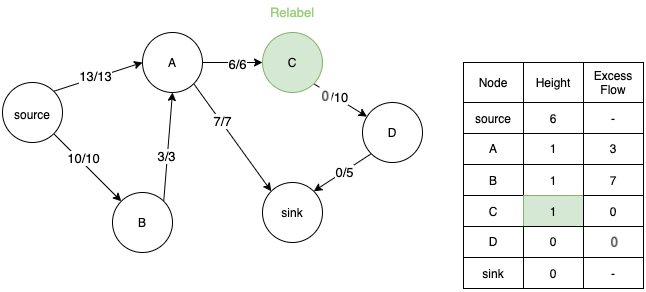
- Hence we relabel node A.
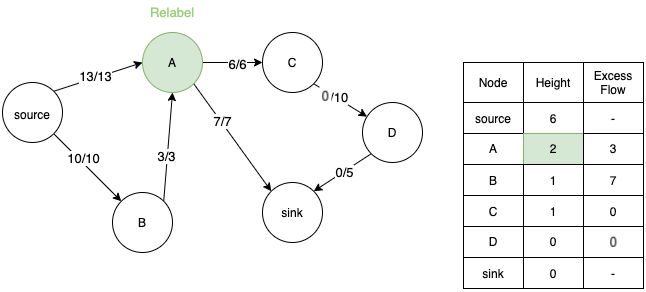
- Since height of A is greater than height of B, it can now push back the extra flow to B.
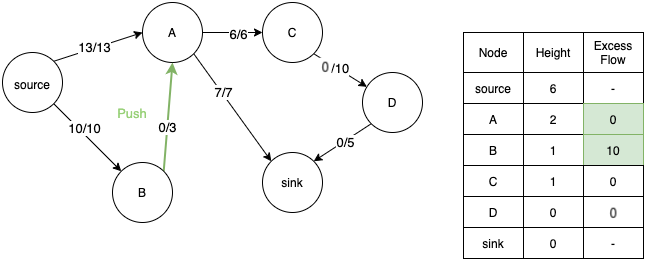
- Since B has no other edge to transfer the flow, we relabel it again and transfer the extra flow back to A.
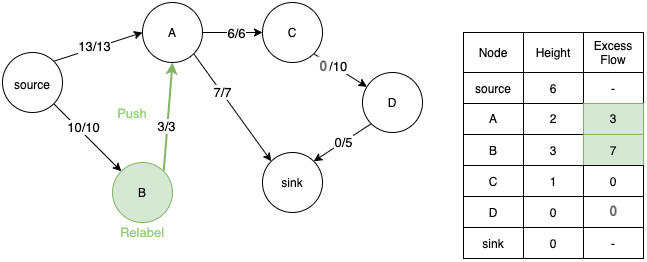
- This to and fro operation between A and B happens till height of B is greater than source node. Now we can push back the extra flow back to source node.
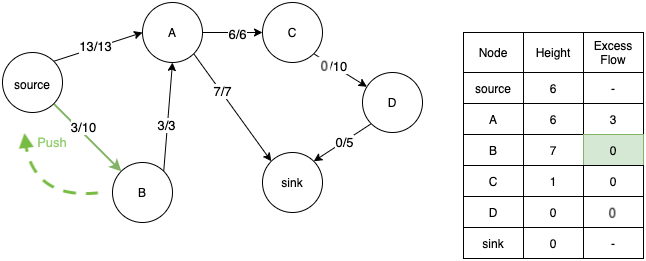
- Similarly, when we relabel A, its height also becomes greater than source and we can push back extra flow to the source. Now both A and B nodes have 0 extra flow.
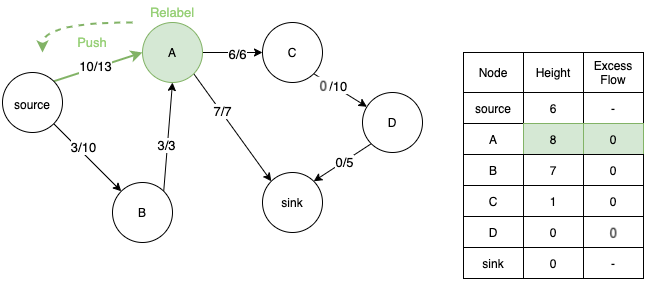
- Now we consider node C and push its extra flow to node D.
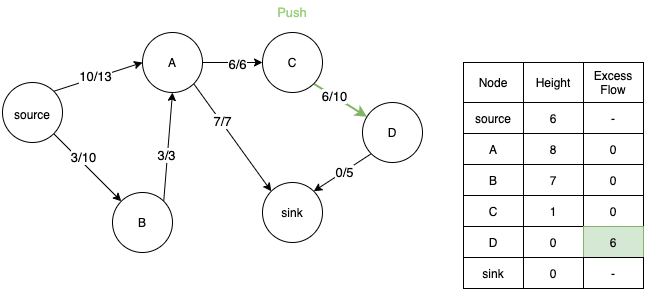
- We relabel D and push its extra flow to sink. However we are still left with 1 unit of extra flow in D.
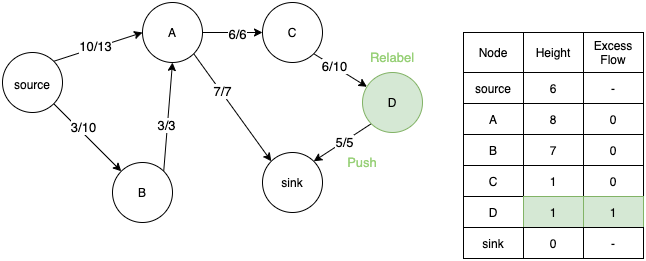
- So, we relabel D again and push back the extra flow to C.
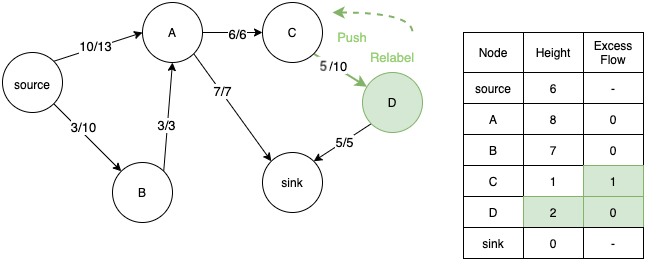
- C again gets relabeled and the flow is pushed back to D. Flow moves to and fro between D and C till height of C becomes greater than A. Then C can push back 1 unit of extra flow to A.
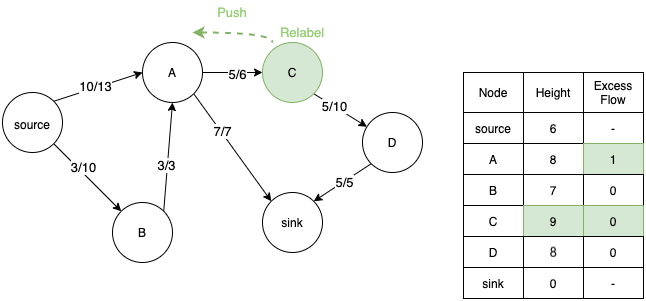
- Since height of A is greater than source, A also pushes back the extra flow to source. Now the extra flow at all the nodes have become 0. The algorithm terminates here.
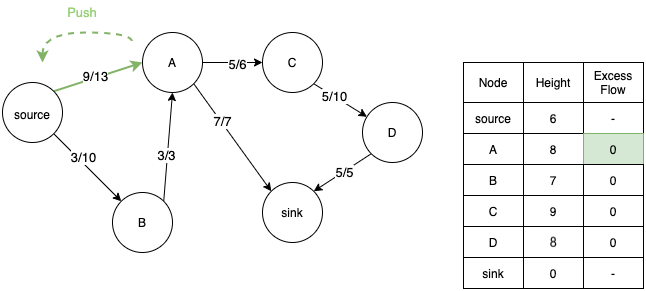
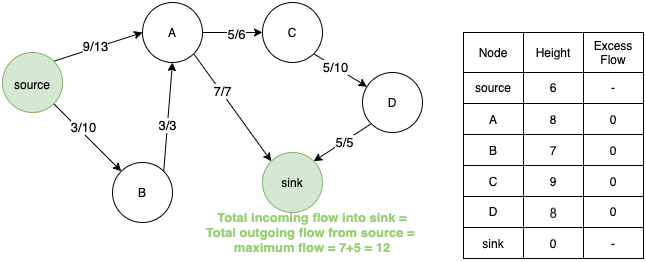
- Maximum flow can be calculated by summing the total outgoing flow from the source or total incoming flow in the sink. In this case it is equal to 12.
Application
Applications of the algorithm are same as any max-flow algorithm, you can read about them here
