
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 10 minutes
Quicksort algorithm is a comparison based sort algorithm based on Divide and Conquer strategy that is it aims to divide a larger problem into smaller problems. It has an average performance of Θ(n*log(n)) and is considered as one of the most efficient sorting algorithms in general when no information is available for the data to be sorted.
Pseudocode
-
Step 1: Choose an element in the list (according to a defined algorithm or randomly) to be the pivot. Consider pivot as the element which will divide the larger problem into a smaller problem
-
Step 2: Partition the list into two sub-lists. One list will have elements with lower values than the pivot and the other list with elements with greater values than the pivot.
At this point, note that the pivot is at the correct location and the left elements are elements smaller than the pivot. The right elements are elements greater than the pivot.
- Step 3: Recursively apply the algorithm to all partitions (left and right subparts)
Example
Consider the following list of integers:
2 4 1 6 5 (we want to sort it in ascending order)
Let us chose 4 as the pivot (step 1)
New lists: (2 1) 4 (6 5) (step 2)
Apply quick sort on (2 1)
Chose 1 as pivot (step 1)
New list from (2 1): (1) (2) (step 2)
Both are one element list so it is sorted
Entire list till now: (1 2 4 6 5)
Apply quick sort on (6 5)
Chose 5 as pivot (Step 1)
New list from (6 5): (5) (6)
Both are one element list so it is sorted
Entire list till now: (1 2 4 5 6)
Entire list is sorted
Visual demonstration of Quick Sort
Note: the black box element is the pivot and the red border elements are the current elements in consideration
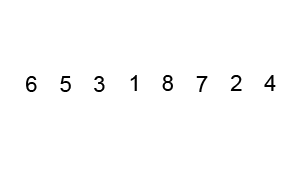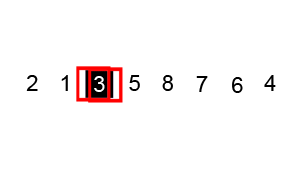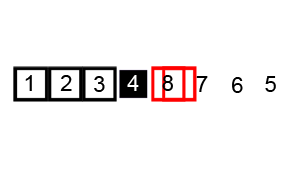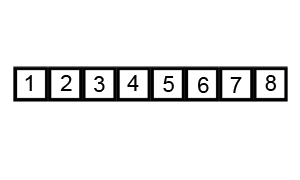
Complexity
- Worst case time complexity:
Θ(N^2) - Average case time complexity:
Θ(N log N) - Best case time complexity:
Θ(N log N)(simple partition);Θ(N)(three way partition) - Space complexity:
Θ(N)(naive);Θ(log N)(Optimized by Sedgewick)
When does the worst case occur?
How to choose the pivot?
The partition can be selected according to any algorithm. The partition algorithm directly impacts the performance of QuickSort. Few of the popular partition algorithms are:
- Pick first element as pivot
- Pick last element as pivot
- Pick a random element as pivot
- Pick median as pivot (considered best)
Picking median as the pivot ensures the worst-case complexity to be O(N log N).
When does the best case occur?
How to partition the elements?
In general, the list is divided into two parts or lists. In case of sorting in ascending order, the first sub-list contains elements less than the pivot and the second sub-list contains elements greater than the pivot.
Partition can be performed in O(N) time complexity.
Implementation
Implementation of Quick Sort algorithm in 5 languages that includes C, C++, Java, Python and C#.
- C
- C++
- Java
- Python
- C#
C
/*Part of Cosmos by OpenGenus Foundation*/
#include <stdio.h>
void swap(int *p, int *q)
{
int temp = *p;
*p = *q;
*q = temp;
}
//Last element is used a spivot
//Places elements smaller than pivot to its left side
//Places elements larger than pivot to its right side
int partition(int a[], int low, int high)
{
int pivot = a[high];
int i = (low - 1);
for (int j = low; j <= high- 1; j++)
{
if (a[j] <= pivot)
{
i++;
swap(&a[i], &a[j]);
}
}
swap(&a[i + 1], &a[high]);
return (i + 1);
}
void quickSort(int a[], int low, int high)
{
if (low < high)
{
int k = partition(a, low, high);
quickSort(a, low, k - 1);
quickSort(a, k + 1, high);
}
}
void print(int a[], int size)
{
int i;
for (i = 0; i < size; i++)
printf("%d ", a[i]);
printf("\n");
}
int main()
{
int n, i;
printf("What is the size of the array?\n");
scanf("%d",&n);
int a[n];
printf("Enter elements of the array one by one\n");
for(i = 0; i < n; i++){
scanf("\n%d",&a[i]);
}
quickSort(a, 0, n - 1);
printf("Sorted array: ");
print(a, n);
return 0;
}
C++
/*
Part of Cosmos by OpenGenus Foundation
quick sort synopsis
namespace quick_sort_impl {
struct quick_sort_tag {};
struct iterative_quick_sort_tag :quick_sort_tag {};
struct recursive_quick_sort_tag :quick_sort_tag {};
template<typename _Random_Acccess_Iter, typename _Compare>
_Random_Acccess_Iter
partition(_Random_Acccess_Iter first, _Random_Acccess_Iter last, _Compare comp);
template<typename _Random_Acccess_Iter, typename _Compare>
void
quickSortImpl(_Random_Acccess_Iter first,
_Random_Acccess_Iter last,
_Compare comp,
std::random_access_iterator_tag,
recursive_quick_sort_tag);
template<typename _Random_Acccess_Iter, typename _Compare>
void
quickSortImpl(_Random_Acccess_Iter first,
_Random_Acccess_Iter last,
_Compare comp,
std::random_access_iterator_tag,
iterative_quick_sort_tag);
}
template<typename _Random_Acccess_Iter, typename _Compare>
void
quickSort(_Random_Acccess_Iter begin, _Random_Acccess_Iter end, _Compare comp);
template<typename _Random_Acccess_Iter>
void
quickSort(_Random_Acccess_Iter begin, _Random_Acccess_Iter end);
*/
#include <stack>
#include <functional>
namespace quick_sort_impl {
struct quick_sort_tag {};
struct iterative_quick_sort_tag :quick_sort_tag {};
struct recursive_quick_sort_tag :quick_sort_tag {};
template<typename _Random_Acccess_Iter, typename _Compare>
_Random_Acccess_Iter
partition(_Random_Acccess_Iter first, _Random_Acccess_Iter last, _Compare comp)
{
_Random_Acccess_Iter i = first, j = last + 1;
while (true)
{
while (i + 1 <= last && comp(*++i, *first))
;
while (j - 1 >= first && comp(*first, *--j))
;
if (i >= j)
break;
std::swap(*i, *j);
}
std::swap(*first, *j);
return j;
}
template<typename _Random_Acccess_Iter, typename _Compare>
void
quickSortImpl(_Random_Acccess_Iter first,
_Random_Acccess_Iter last,
_Compare comp,
std::random_access_iterator_tag,
recursive_quick_sort_tag)
{
if (first < last)
{
// first is pivot
auto mid = quick_sort_impl::partition(first, last, comp);
quickSortImpl(first,
mid - 1,
comp,
std::random_access_iterator_tag(),
recursive_quick_sort_tag());
quickSortImpl(mid + 1,
last,
comp,
std::random_access_iterator_tag(),
recursive_quick_sort_tag());
}
}
template<typename _Random_Acccess_Iter, typename _Compare>
void
quickSortImpl(_Random_Acccess_Iter first,
_Random_Acccess_Iter last,
_Compare comp,
std::random_access_iterator_tag,
iterative_quick_sort_tag)
{
if (first < last)
{
std::stack<std::pair<_Random_Acccess_Iter, _Random_Acccess_Iter>> st;
st.push(std::make_pair(first, last));
while (!st.empty())
{
_Random_Acccess_Iter left, right, i, j;
left = st.top().first;
right = st.top().second;
st.pop();
// ignore if only one elem
if (left >= right)
continue;
auto mid = quick_sort_impl::partition(left, right, comp);
st.push(std::make_pair(left, mid - 1));
st.push(std::make_pair(mid + 1, right));
}
}
}
}
template<typename _Random_Acccess_Iter, typename _Compare>
void
quickSort(_Random_Acccess_Iter begin, _Random_Acccess_Iter end, _Compare comp)
{
using namespace quick_sort_impl;
if (begin == end)
return;
--end;
auto category = typename std::iterator_traits<_Random_Acccess_Iter>::iterator_category();
return quickSortImpl(begin, end, comp, category, iterative_quick_sort_tag());
}
template<typename _Random_Acccess_Iter>
void
quickSort(_Random_Acccess_Iter begin, _Random_Acccess_Iter end)
{
using value_type = typename std::iterator_traits<_Random_Acccess_Iter>::value_type;
return quickSort(begin, end, std::less<value_type>());
}
Java
// Part of Cosmos by OpenGenus Foundation
class QuickSort {
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // last element is the pivot
int i = (low - 1);
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) { // if j'th element is less than or equal to the pivot
i++; // then swap the i'th element with the j'th element
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// swap arr[i+1] and arr[high] (or pivot)
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1; // return position of the pivot
}
void sort(int arr[], int low, int high) {
if (low < high) {
// after the following function call elemnt at positon pi
// is at it's correct poition in the sorted array
int piv = partition(arr, low, high);
sort(arr, low, piv - 1); // recursively sort
sort(arr, piv + 1, high); // rest of the array
}
}
static void printArray(int arr[]) {
int n = arr.length;
for (int i = 0; i < n; ++i) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String args[]) {
int arr[] = {5, 7, 11, 56, 12, 1, 9};
int n = arr.length;
QuickSort qso = new QuickSort();
qso.sort(arr, 0, n - 1);
System.out.println("sorted array");
printArray(arr);
}
}
Python
'''
Part of Cosmos by OpenGenus Foundation
'''
def quick_sort(arr):
quick_sort_helper(arr, 0, len(arr) - 1)
def quick_sort_helper(arr, first, last):
if first < last:
splitpoint = partition(arr, first, last)
quick_sort_helper(arr, first, splitpoint - 1)
quick_sort_helper(arr, splitpoint + 1, last)
def partition(arr, first, last):
pivot = arr[first]
left = first + 1
right = last
done = False
while not done:
while left <= right and arr[left] <= pivot:
left = left + 1
while arr[right] >= pivot and right >= left:
right = right -1
if right < left:
done = True
else:
temp = arr[left]
arr[left] = arr[right]
arr[right] = temp
temp = arr[first]
arr[first] = arr[right]
arr[right] = temp
return right
C#
using System;
using System.Collections.Generic;
/*
* Part of Cosmos by OpenGenus Foundation
*/
namespace ConsoleApplicationQSort
{
class Program
{
static void Main(string[] args)
{
var A = new int[] { 9, 8, 7, 6, 5, 4, 3, 2, 1 };
var sorter = new QSort<int>(A);
sorter.Sort();
foreach (var i in sorter.A)
Console.WriteLine(i);
Console.Read();
}
}
class QSort<T> where T:IComparable
{
public IList<T> A;
public QSort(IList<T> A)
{
this.A = A;
}
public int Partition(int L, int U)
{
int s = U;
int p = L;
while (s != p)
{
if (A[p].CompareTo(A[s]) <= 0)
{
p++;
}
else
{
Swap(p, s);
Swap(p, s - 1);
s--;
}
}
return p;
}
private void Swap(int p, int s)
{
T tmp = A[p];
A[p] = A[s];
A[s] = tmp;
}
public void Sort(int L, int U)
{
if (L >= U) return;
int p = Partition(L, U);
Sort(L, p-1);
Sort(p + 1, U);
}
public void Sort()
{
Sort(0, A.Count - 1);
}
}
}
What is 3-Way QuickSort?
In QuickSort algorithm, we select an element as pivot and partition the array around pivot and recur for subarrays on left and right of pivot.
Consider an array which has many redundant elements. For example, {1, 4, 2, 4, 2, 4, 1, 2, 4, 1, 2, 2, 2, 2, 4, 1, 4, 4, 4}. If 4 is picked as pivot in Simple QuickSort, we fix only one 4 and recursively process remaining occurrences.
In 3 Way QuickSort, an array arr[l..r] is divided in 3 parts:
- arr[l..i] elements less than pivot.
- arr[i+1..j-1] elements equal to pivot.
- arr[j..r] elements greater than pivot.
Consider the following implementation of 3-way quick sort:
/* Part of Cosmos by OpenGenus Foundation */
#include <vector>
#include <stdlib.h>
#include <iostream>
using namespace std;
/* UTILITY FUNCTIONS */
void swap(int &a, int &b)
{
int temp = a;
a = b;
b = temp;
}
void printarr(vector<int> &v)
{
for (size_t i = 0; i < v.size(); ++i)
cout << v[i] << " ";
cout << endl;
}
void fill(vector<int> &v, int max)
{
for (size_t i = 0; i < v.size(); ++i)
v[i] = rand() % max + 1;
}
// three-way-partioning
void partition(vector<int> &v, int low, int high, int &i, int &j)
{
if (high - low <= 1)
{
if (v[high] < v[low])
swap(v[high], v[low]);
i = low;
j = high;
return;
}
int mid = low;
int pivot = v[high];
while (mid <= high)
{
if (v[mid]<pivot)
swap(v[low++], v[mid++]);
else if (v[mid] == pivot)
mid++;
else if (v[mid] > pivot)
swap(v[mid], v[high--]);
}
i = low - 1;
j = mid;
}
void quicksort(vector<int> &v, int low, int high)
{
if (low >= high)
return;
int i, j;
partition(v, low, high, i, j);
// Recursively sort two halves
quicksort(v, low, i);
quicksort(v, j, high);
}
// Driver program
int main()
{
int size = 10;
int maxRand = 10;
cout << "Input test array size: ";
cin >> size;
vector<int> v(size);
cout << "Maximum random number: ";
cin >> maxRand;
fill(v,maxRand);
cout << "Unsorted: ";
printarr(v);
quicksort(v, 0, size - 1);
cout << "Sorted: ";
printarr(v);
return 0;
}
Optimizations
Two other important optimizations, also suggested by Sedgewick and widely used in practice are:
-
To make sure at most O(log n) space is used, recurse first into the smaller side of the partition followed by a tail call to recurse into the other.
If the number of elements is less than 10, use a non-recursive sorting algorithm such as insertion sort that performs fewer swaps, comparisons or other operations on such small arrays. -
When the number of elements is less than a threshold
k, keep it on hold until the whole array has been processed. Then, perform insertion sort on it. Stopping the recursion early leaves the array k-sorted, meaning that each element is at most k positions away from its final sorted position. In this case, insertion sort takes O(kn) time to finish the sort, which is linear if k is a constant. This makes suboptimal use of the cache memories in modern architectures.
Applications
-
Quicksort is used everywhere where a stable sort is not needed
-
Variants of quicksort are used to separate the k smallest or largest elements
-
Quicksort's divide-and-conquer enables the use of parallelization
-
Quick Sort is a cache friendly sorting algorithm as it has good locality of reference when used for arrays
-
Quick Sort is tail recursive and hence, all tail call optimizations can be done
-
Quick Sort is an in-place sort that is does not require any extra storage
For any doubts, ask questions in the discussion below
