
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will be developing and implementing an algorithm that recovers a Binary Search Tree (BST) that had two of its nodes swapped accidentally.
Table of contents:
- Examining the Problem Statement
- Solving the Problem
- Find two swapped elements in a sorted array
- Conclusion
To practice more Binary Tree problems, go through this list of Binary Tree Problems.
This is similar to Leetcode Problem 99. Recover Binary Search Tree. Let us get started with Recovering a Binary Search Tree that has two nodes swapped.
Examining the Problem Statement
As always, before we start implementing a solution to a problem we should ensure that we have a deep understanding of the problem. Let us begin by defining an explicit problem statement.
Given the root of a Binary Search Tree where exactly two of its nodes have accidentally been swapped. Recover the BST without changing the structure of the tree.
Okay, we now have a well-defined problem statement, we know that we are to recover a BST but what exactly is a BST?
A binary search tree is a binary tree data structure where each node contains a key and it maintains some special properties:
- All the nodes in the left subtree of a node have keys less than the node's key
- All the nodes in the right subtree of a node have keys greater than the node's key.
- The left and right subtrees are also binary search trees
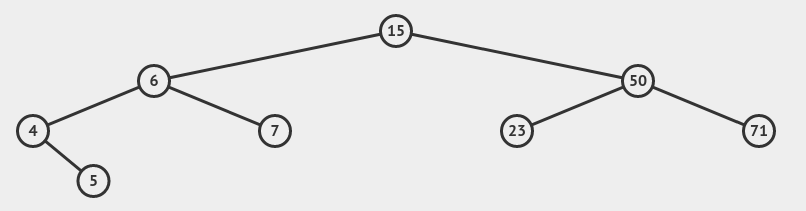
An Example of a BST
Binary search trees are cool data structures that are useful for insertion, lookup and deletion. All the mentioned operations have a time complexity of O(h) where h is either equal to log(n) for the average and best case of the tree being balanced or h is equal to n in the worst-case scenario where the tree is not balanced.
Solving the Problem
To recover a BST we have to first find the offending nodes and then swap their values so that the BST properties are preserved. Let's look at possible strategies we can employ to find the swapped nodes.
To find the offending nodes we have to be able to move through each node in the tree and read their keys. Moving through a tree is known as tree traversal. There are two ways to traverse a tree either depth-first or breadth-first.
Breadth-first traversal entails traversing the tree level by level. You start from the root and then visit the immediate children of the root and then the immediate children of the immediate children and so on. While in depth-first you always push through the levels until you get to a leaf node and then backtrack. There are 3 types of depth-first traversals.
- Inorder traversal
- Preorder traversal
- Postorder traversal
For this problem, we are only interested in Inorder traversal. In the inorder traversal we recursively explore the left subtree, then the root then the right subtree.
Why are we interested in the inorder traversal of the tree? Because the inorder traversal of a correct BST will give a list of nodes sorted in increasing order of keys. This is an interesting property to note that will help us to solve the problem.
Implementation of the Inorder traversal of a tree in Python:
class BST:
""" representation of a binary search tree"""
def __init__(self, val):
self.val = val
self.left = None
self.right = None
def inordertraversal(rootnode):
""" store the inorder traversal of a bst in a list and return it """
nodesInorder = []
def inorder(node):
""" recursive function that stores the inorder traversal into a list """
if not node:
return
else:
# inorder traversal left-node-right
inorder(node.left)
nodesinorder.append(node)
inorder(node.right)
# call the recursive function and populate the list
inorder(rootnode)
return nodesinorder
We then proceed to get the inorder traversal list of our damaged BST. Create a copy of the list, sort the copy and compare it with the original to find the two offending nodes and then swap them, therefore, restoring the tree. This approach will take a time complexity of O(N logN).
Alternatively, since we know that only two entries on the list are in the wrong positions. The problem can be reduced to a problem of finding two swapped elements in a sorted array. Which can be solved in one pass with a time complexity of O(n)
Find two swapped elements in a sorted array
We have an almost sorted list [3, 10, 5, 6, 4, 14]. We can intuitively see that the values of 10 and 4 are swapped. The swap interrupts the flow of the numbers in the list, the numbers are supposed to be in increasing order but at two points, 10, 5 and 6, 4 this property is violated.
To find the faulty nodes we iterate through the list checking for when the value at position i is greater than the value at position i + 1 which indicates that the increasing property has been violated. The first time we encounter this we store position i (The bigger number) in a separate faulty list and the second time we encounter this we store the position i + 1. We then swap the values at the positions.
An edge case for the above algorithm is when the two swapped values are adjacent to each other. In this case, the loop will never find the 2nd violation of the increasing property of the list. We can easily mitigate this by adding a check at the end of the iteration, if there is only one number in the faulty list that means the next number is adjacent so add it to the list and swap.
The Implementation
def restoreOrder(listofnodes):
faultylist = []
# add the index of the bigger of the swapped nodes
for i in range(0, len(listofnodes) - 1):
if listofnodes[i].val > listofnodes[i + 1].val:
faultylist.append(i)
break
# add the index of the smaller of the swapped nodes
for j in range(faultylist[0] + 1, len(listofnodes) - 1):
if listofnodes[j].val > listofnodes[j + 1].val:
faultylist.append(j + 1)
break
# check for edgecase where nodes are adjacent
if len(faultylist) == 1:
faultylist.append(faultylist[0] + 1)
# swap the value of the nodes
node1 = listofnodes[faultylist[0]]
node2 = listofnodes[faultylist[1]]
node1.val, node2.val = node2.val, node1.val
Conclusion
We have been able to solve the problem of two wrongly swapped nodes in a BST by taking advantage of an inherent property of trees, the fact that the inorder traversal of a tree results in a sorted list. We then used this propety to reduce the problem to a much simpler one of finding two swapped node in a sorted list. Allowing us to fully solve the problem in linear time.
