In this article, we have explored the Reverse Delete Algorithm for finding Minimum Spanning Tree (MST).

Prerequisite: What is Minimum Spanning Tree?

Table of content:

1. Introduction to Spanning Tree
2. Reverse Delete Algorithm
3. Step by Step Example
4. Time and Space Complexity
5. Implementation of Reverse Delete Algorithm
6. Application of Reverse Delete Algorithm

Introduction to Spanning Tree

Let's get started with Spanning Tree.
A spanning tree of a graph, is a sub-graph with same number of vertices but with minimum number of edges to keep the graph connected (Connected means we can visit all the vertices from any node).

A minimum spanning tree(MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted directed or undirected graph that connects all the vertex, without any cycles and with the minimum possible total edge weight. It is a spanning tree whose sum of edge weights is as small as possible.

Ideally, for finding MST we would have started first by adding the smallest edge and moved up to the largest edge (like Kruskal MST Algorithm ).

Reverse Delete Algorithm

In Reverse Delete Algorithm, we sort all edges in decreasing order of their weights. We then pick each edge from the sorted list and remove it from the graph, if removing it keeps the graph connected, we continue, else we add the edge again.

Algorithm/ Steps of Reverse Delete Algorithm:

1. Sort all edges in decreasing order of their weights.
2. Intiailize the MST as original Graph.
3. Iterate the edges and do the following:
   3.1 Remove the current edge from the graph
   3.2 Check if removing the edge disconnects the graph:
   If it does add the removed edge else
   If it does not means that the edge can be removed
   (which we did step 3.1) and we go ahead to check the other edges

Step by Step Example

Consider this graph:
The numbers near the edge indicate their edge weight

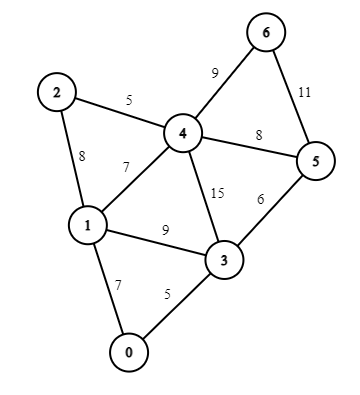
Minimum Spanning Tree of this graph is :

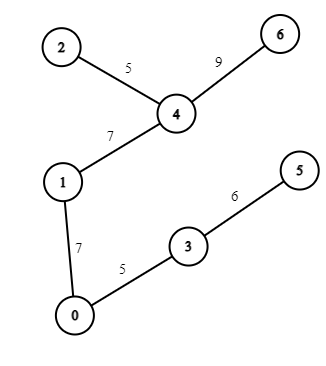
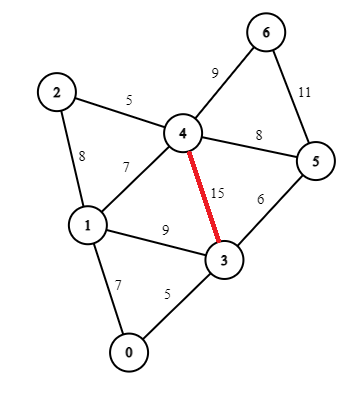
Let's run the Reverse Delete Algorithm on the Graph:

• We start with the edge with highest weight i.e. Edge 3 to 4.

• Since, deleting the edge 3-4 does not disconnect the graph, so the edge can be removed.
  

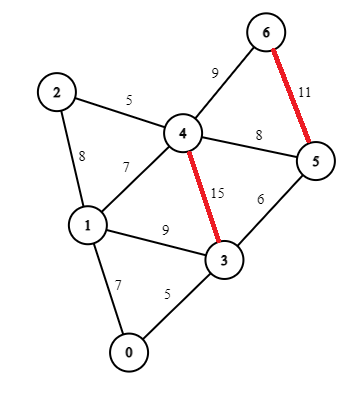
• Next select the edge 5-6 with weight 11. Since, deleting the edge 5-6 does not disconnect the graph, so the edge can be removed.

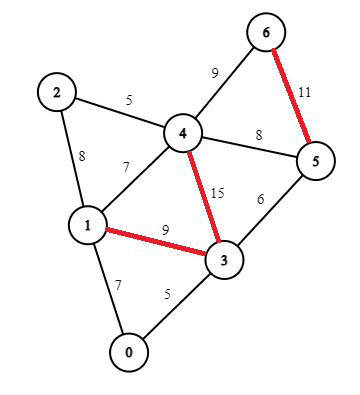
• Select the edge 1-3 with weight 9. Since, deleting the edge 1-3 does not disconnect the graph, so the edge can be removed.

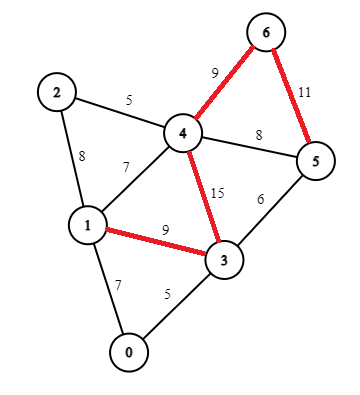
• Next select the edge 4-6 with weight 9. Deleting this edge will result in the graph being disconnected, as Node 6 gets seperated. So, we do not delete the edge.

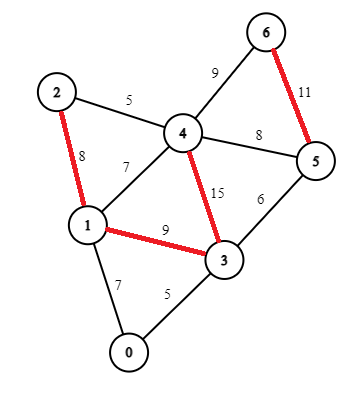
• Next select the edge 1-2 with weight 8. Since, deleting the edge 1-2 does not disconnect the graph, so the edge can be removed.

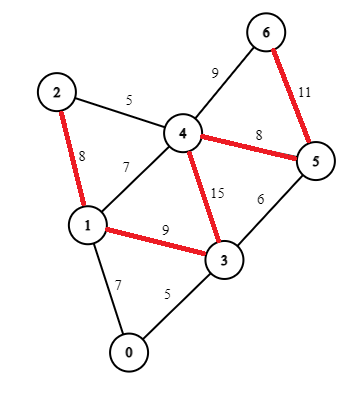
• Next select the edge 4-5 with weight 8. Since, deleting the edge 4-5 does not disconnect the graph, so the edge can be removed.
• If you check the MST for this graph it matches the one we have here.
• The algorithm will then search the remaining edges and will not find another edge to delete; therefore this is the final graph returned by the algorithm.

Time and Space Complexity

• Time Complexity:

1. Sorting the edges takes: O(E * Log(E))
2. Deleting an edge from an adjacency list take O(V). This can be optimised by using unordered_set.
3. DFS on a graph takes O(V+E)
4. Steps 2 and 3 will be done for each Edge and thus complexity will be O(E * (V+E))

Total Time Complexity:

O( E * Log(E) + E * (V+E)). It can be also expressed as O(E * (V+E+Log(E))

• Space Complexity: O(V+E)

Implementation of Reverse Delete Algorithm

C++

unordered_map<int,unordered_set<int>> graph : Stores Node having edge from U to V.

vector<pair<int, pair<int, int>>> edges : Storing weight W and edges from Node U to V.

#include <bits/stdc++.h>
#define ll long long int
#define ld long double
#define mk make_pair
#define pb push_back
#define MOD 1000000007
#define fo(i, a, b) for (i = a; i < b; i++)
#define boost                    \
    ios::sync_with_stdio(false); \
    cin.tie(0)
using namespace std;

// Adding u to v nodes to the graph and weight between them
void AddWeightedEdge(unordered_map<int, unordered_set<int>> &graph, vector<pair<int, pair<int, int>>> &edges, int u, int v, int w)
{
    graph[u].insert(v);
    graph[v].insert(u);
    edges.push_back({w, {u, v}});
}

// DFS on the node
void DFS(unordered_map<int, unordered_set<int>> &graph, vector<bool> &visited, int node)
{
    visited[node] = 1;
    for (auto neighbour : graph[node])
    {
        if (!visited[neighbour])
        {
            DFS(graph, visited, neighbour);
        }
    }
}

// Checking if the graph is connected after removing the edge
bool checkConnected(unordered_map<int, unordered_set<int>> &graph, int V)
{
    // vector to keep track of visited and initialized to 0
    vector<bool> visited(V, 0);

    // Starting DFS from node 0
    DFS(graph, visited, 0);

    // Checking if each node is visited. If a node is not visited that means the graph is disconnected and we return 0
    // The removed edge needs to be added again
    for (int i = 0; i < V; i++)
        if (visited[i] == 0)
            return 0;

    // If all nodes are visited removing the edge does keep the graph connected
    return 1;
}

void reverseDeleteMST(unordered_map<int, unordered_set<int>> &graph, vector<pair<int, pair<int, int>>> &edges, int V)
{
    // Sorting the edges
    sort(edges.begin(), edges.end());

    // Weight of the MST
    int mstWeight = 0;
    int u, v;

    for (int i = edges.size() - 1; i >= 0; i--)
    {
        u = edges[i].second.first;
        v = edges[i].second.second;

        // Deleting the edge from the graph
        graph[u].erase(v);
        graph[v].erase(u);

        // Check if the graph is connected after removing the edge
        if (checkConnected(graph, V) == 0)
        {
            // Re-adding the edge as the graph gets disconnected
            graph[u].insert(v);
            graph[v].insert(u);

            cout << "Edge : " << u << " " << v << "\n";
            mstWeight += edges[i].first;
        }
    }
    cout << "Weight of MST is : " << mstWeight << "\n";
}

int main()
{
    int V = 7;
    unordered_map<int, unordered_set<int>> graph;
    vector<pair<int, pair<int, int>>> edges;

    // Adding nodes to the graph and edges
    // Same graph as the one in the example
    AddWeightedEdge(graph, edges, 0, 1, 7);
    AddWeightedEdge(graph, edges, 0, 3, 5);
    AddWeightedEdge(graph, edges, 1, 2, 8);
    AddWeightedEdge(graph, edges, 1, 4, 7);
    AddWeightedEdge(graph, edges, 1, 3, 9);
    AddWeightedEdge(graph, edges, 3, 4, 15);
    AddWeightedEdge(graph, edges, 3, 5, 6);
    AddWeightedEdge(graph, edges, 2, 4, 5);
    AddWeightedEdge(graph, edges, 4, 5, 8);
    AddWeightedEdge(graph, edges, 4, 6, 9);
    AddWeightedEdge(graph, edges, 5, 6, 11);

    // Calling reverse Delete MST
    reverseDeleteMST(graph, edges, V);
}

Application of Reverse Delete Algorithm

Applications of Reverse Delete Algorithm for MST are:

• Used to find the Minimum Spanning Tree using a greedy approach
• Designing Local Area Networks
• See Applications of Minimum Spanning Tree

With this article at OpenGenus, you must have the complete idea of Reverse Delete Algorithm.