Reading time: 40 minutes

Given a weighted directed graph, we need to find the shortest path from source u to the destination v having exactly k edges.

We use adjacency matrix to represent the graph in which value of adj[i][j] represents if there is an edge from vertex i to vertex j in the graph. If the value is w{w:Integer} then there is an edge from vertex i to vertex j with a weight of w else, if the value is INF then there is no edges from vertex i to vertex j in the graph.

This problem is similar to finding number of path from source to destination with k edges in which we have to find total number of paths, now for this problem the shortest path will be one of the total number of paths with lowest weight cost.
To understand this problem, let's take an example of directed graph with 6 vertices {0, 1, 2, 3, 4, 5}, and 9 weighted edges between them.

Now to find the shortest path between 0 and 3 having exactly 3 edges between them, let's analyse the diagram of graph given below:

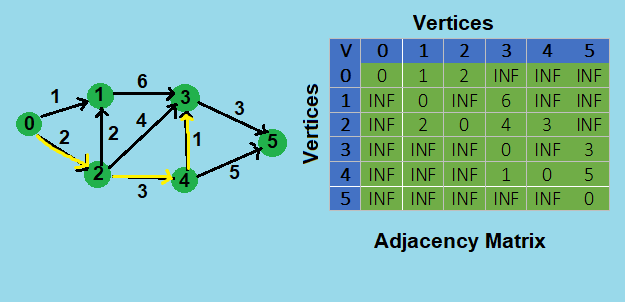
from the graph we can see that there are two paths from 0 to 3, 0-->2-->1-->3 and 0-->2-->4-->3. From which the shortest path is 0-->2-->4-->3, whose cost is 6.

To solve this problem, we will see two approaches, one is brute force approach which takes O(V^k) time and the other is dynamic programming approach which takes O(V³k) time.

Brute Force approach

This is the simple way to start from the source, go to all the adjacent vertices and recur for adjacent vertices for k as k-1, source as adjacent vertices. We maintain a cost variable which stores the lowest cost to reach from u to j, and recursively solve it for u to v. When k becomes 0 and we reach to the destination, we compare the current cost with the minimum cost and return the optimal one.

int shortestPathNaive(std::vector< std::vector<int> > adj, int u, int v, int k)
{
    int __v = adj.size();
    if(k == 0 && u == v)
        return 0;
    if(k == 1 && adj[u][v] != INF)
        return adj[u][v];
    if(k <= 0)
        return INF;
    int res = INF;
    for(int i = 0; i < __v; ++ i)
    {
        if(u == i || v == i)
            continue;
        if(adj[u][i] != INF)
        {
            res = std::min(res, sortestPathNaive(adj, i, v, k - 1) + adj[u][i] );
        }
    }
    return res;
}

The above algorithm recur for all the paths possible and choses the optimal one, so in the worst case it runs in O(V^k) time as we need to go through all the vertices and recur for their adjacent vertices k times to find the shortest path.

Dynamic Programming approach

We can efficiently solve this problem in O(V³k) time using dynamic programming.
In dynamic programing approach we use a 3D matrix table to store the cost of shprtest path, dp[i][j][e] stores the cost of shortest path from i to j with exactly e edges.
We fill the table in bottom up manner, we start from e=0 and fill the table till e=k. Then we have our shortest path cost stored in dp[u][v][k] where u is source, v is destination and k is number edges between path from source to destination.
Here we use the recurrence as:

if (e > 1)
   for (int b = 0; b < __v; ++b)
        if (adj[i][b] != INF && i != b)
            dp[i][j][e] = std::min(dp[i][j][e], dp[b][j][e - 1] + adj[i][b] );

The above approach takes O(V³k) time in worst case.

Implementation

Code in C++11

// C++ code to find the shortest path from source to destination
// with k edges between them using DP.
#include<iostream>
#include<vector>
#include<algorithm>
#define INF 1<<27

int shortestPathdp(std::vector<std::vector<int>> adj, int u, int v, int k)
{
    int __v = adj.size();
    int dp[__v][__v][k + 1];

    for (int e = 0; e <= k; ++e)
    {
        for (int i = 0; i < __v; ++i)
        {
            for (int j = 0; j < __v; ++j)
            {
                // initialize
                dp[i][j][e] = INF;

                // base cases
                if (e == 0 && i == j)
                    dp[i][j][e] = 0;
                if (e == 1 && adj[i][j] != INF)
                    dp[i][j][e] = adj[i][j];

                // go to adjacent edges only when number of edges is more than 1
                if (e > 1)
                {
                    for (int b = 0; b < __v; ++b)
                    {
                        if (adj[i][b] != INF && i != b)
                        {
                            dp[i][j][e] = std::min(dp[i][j][e], dp[b][j][e - 1] + adj[i][b] );
                        }
                    }
                }
            }
        }
    }
    // shortest path from u to v with k edges
    return dp[u][v][k];
}
int main()
{
    int _v, e;
    std::cin >> _v >> e;
    std::vector<std::vector<int>> adj(_v, std::vector<int>(_v, INF));
    int u, v, w;
   // std::cout<<adj[0][3]<< " "<<adj[4][5] <<" \n";
    for (int i = 0; i < e; ++i)
    {
        std::cin >> u >> v >> w;
        adj[u][v] = w;
    }
    int k;
    std::cin >> u >> v >> k;
    int res = shortestPathdp(adj, u, v, k);
    if(res == INF)
        std::cout << "INF\n";
    else
    std::cout << res << "\n";
    return 0;
}

Sample Input and Output

// Input
6 9  // vertices=6 edges=9
0 1 1  // edge{0-->1} and weight 1
0 2 2
1 3 6
2 1 2
2 3 4
2 4 3
4 3 1
3 5 3
4 5 5
0 3 3  // source=0 destination=3 k=3
// Output
6  // shortest path cost

Complexity

Time Complexity

• Brute force approach takes O(V^k) time.
• DP approach takes O(V³k) time.

Space Complexity

• Brute force approach takes O(V²) auxiliary space and O(V^k) stack space.
• DP approach takes O(V²k) auxiliary space.