Squeeze and Excitation (SE) Block

• Introduction
• Brief overview of CNN
• Understanding the SE Block
• Applications of the SE Block
• Performance and Model complexity
• Benefits of the SE Block
• Alternatives to SE blocks
• Conclusion
• References

Introduction

Convolutional Neural Networks (CNNs) have revolutionized the field of computer vision by achieving remarkable results in various tasks, such as image classification, object detection, and semantic segmentation. To further enhance the power of CNNs, researchers have proposed novel architectural units, one of which is the Squeeze and Excitation (SE) block. In this article, I will explore the concept and benefits of the SE block and how it can be used.

Brief overview of CNN

Convolutional neural networks (CNNs) are a highly effective type of neural network primarily used for image classification tasks. They are composed of three main types of layers: convolutional layers, pooling layers, and fully connected layers. Convolutional layers apply a kernel matrix over the input data to create feature maps for subsequent layers. These kernels can be adjusted to produce different feature maps or modify the size and dimensions of the data. The feature map values are typically computed using a sum of element-wise multiplications between the kernel and corresponding sections of the input data.

Here is an example of a convolution:

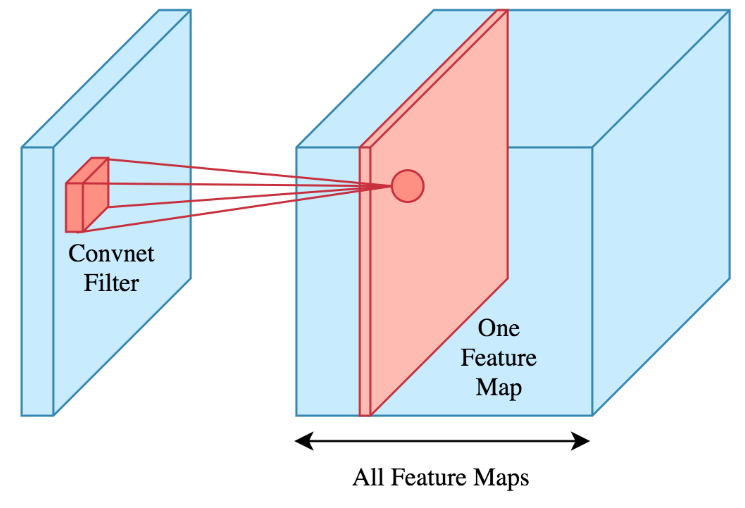
By stacking multiple of the above mentioned layers the performance of the CNN is improved. Here is an example of a CNN with many layers:

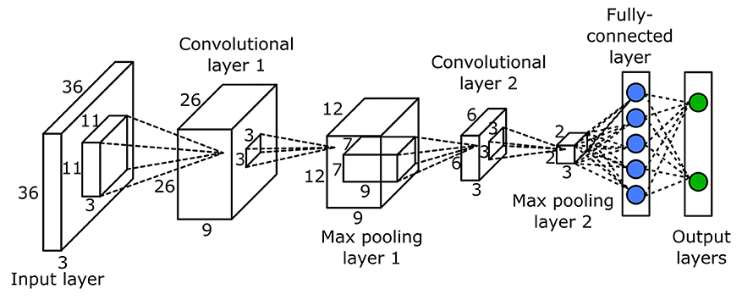
Understanding the SE Block

Traditional convolutional operations in CNNs fuse both spatial and channel-wise information. Spatial information refers to the relationships between neighboring pixels or regions within an image, while channel-wise information refers to the relationships between different channels or feature maps in a CNN.

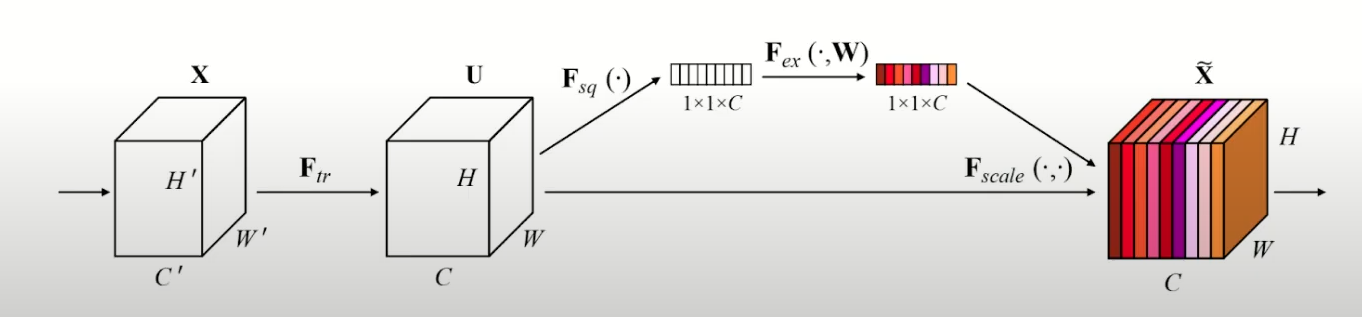
The SE block focuses specifically on improving the channel relationship. It introduces a mechanism to capture and emphasize important channel-wise information, enabling CNNs to better discriminate and learn relevant features.

Squeezing Step

The SE block consists of two main parts:

• squeezing
• exciting

The squeezing step involves capturing global spatial information by performing pooling function (generally average pooling because its the simplest, but max pooling could also work etc). This operation reduces the spatial dimensions of feature maps to a single-channel representation, aiming to summarize the information across the entire spatial extent.

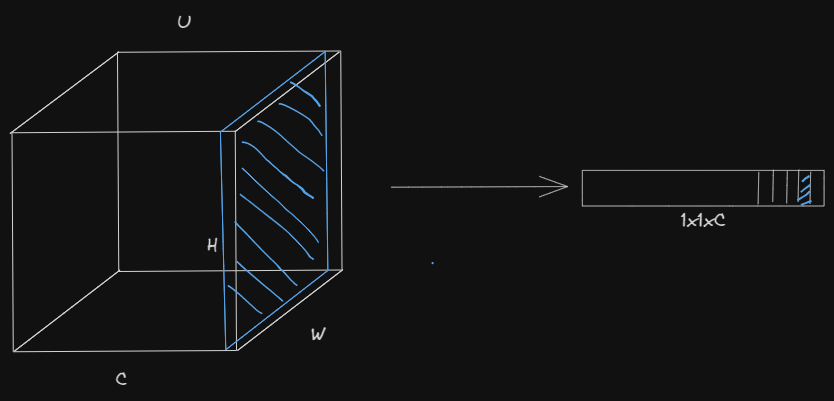
The global average pooling operation aggregates the spatial information into a 1x1xC tensor, where C represents the number of channels in the input feature maps.

Mathematically the global average pooling returns the statistic z for each channel c by summing up the "pixel values" in the given channel and dividing by the total number of pixels in that channel, for a channel with Hight H and width W the formula is:

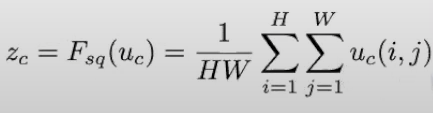
The number of operations (Ops) involved in the global average pooling is relatively low compared to convolutional operations.

Exciting Step

After the squeezing step, the exciting step follows, where channel-wise dependencies are modeled and enhanced. The single-channel representation obtained from the squeezing step is passed through a set of fully connected layers. These layers act as a gating mechanism, learning to assign importance weights to each channel based on their relevance to the task at hand. The computed weights are then used to rescale the original feature maps, giving higher weights to more important channels and lower weights to less important ones.

Here the shade of red represents the weight for the different channels.

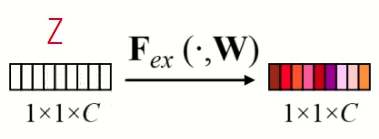
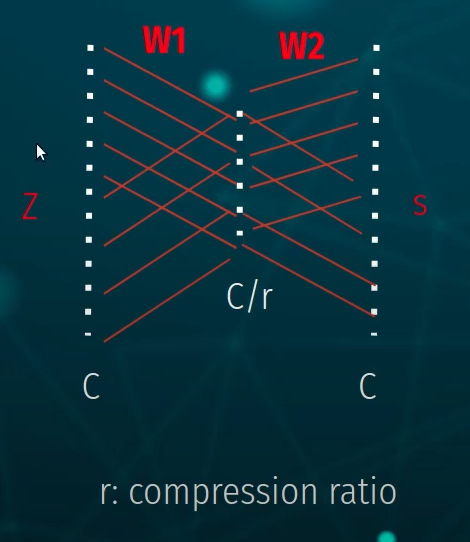
Here is an illustration of the fully connected layers, taking the input vector Z with shape 1x1xC compressing it with the compression ratio r and then scaling it back up.

mathematically we can express this operations as:

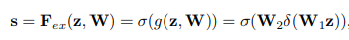
Where $\delta$ refers to the ReLU function and $\sigma$ refers to the sigmoid function. W_1 and W_2 refers to the weights in the fully connected layers forming a bottleneck with around the "dimensionality-reduction layer" with reduction ratio r. s are the outputted filter weights.

The final output of the block is obtained by rescaling the original filter maps with the obtained filter weights through channel-wise multiplication.

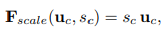
Applications of the SE Block

The SE block has been successfully incorporated into various CNN architectures, resulting in improved performance across different computer vision tasks. Here are some models where the SE block has been used:

1. SE-ResNet: The SE block was first introduced in the ResNet architecture, leading to the development of SE-ResNet models. SE-ResNet models have shown improved accuracy in image classification tasks compared to the original ResNet models. The SE block allows the network to adaptively emphasize informative channels, enhancing the discriminative power of the model.

2. SE-DenseNet: The SE block has also been integrated into DenseNet, resulting in SE-DenseNet models. DenseNet models are known for their dense connectivity patterns, and the addition of SE blocks further improves their performance. SE-DenseNet models have achieved state-of-the-art results in image classification tasks by effectively capturing channel-wise dependencies.

3. SE-MobileNet: MobileNet is a lightweight CNN architecture designed for mobile and embedded devices. By incorporating the SE block into MobileNet, researchers have created SE-MobileNet models, which achieve improved accuracy in image classification while maintaining the efficiency and compactness of the original MobileNet architecture.

4. SENet: SENet (Squeeze-and-Excitation Network) is a standalone architecture that utilizes the SE block as its core building block. SENet models have achieved impressive results in various computer vision tasks, including image classification, object detection, and semantic segmentation. The SE block enhances the feature representation capabilities of SENet, leading to improved performance across different datasets and benchmarks.

These models have been applied to a wide range of computer vision tasks:

• Image Classification: The SE block has been primarily used in image classification tasks, where the goal is to assign a label to an input image. By incorporating the SE block into CNN architectures, models have achieved higher accuracy and better discrimination, resulting in improved image classification performance.

• Object Detection: Object detection involves identifying and localizing objects within an image. CNN models with the SE block have been applied to object detection tasks, resulting in improved object detection accuracy. The SE block enhances the ability of the models to capture discriminative features, leading to more accurate object localization and classification.

• Semantic Segmentation: Semantic segmentation aims to assign a semantic label to each pixel in an image, dividing the image into meaningful regions. CNN models with the SE block have been used in semantic segmentation tasks, improving the ability of the models to capture fine-grained details and accurately segment objects of interest.

• Generative Models: The SE block has also found applications in generative models, which aim to generate new samples similar to a given dataset. By incorporating the SE block into generative models, researchers have achieved better feature representation, resulting in improved sample generation quality.

Here are two examples of how the RE has been added to the Inception and Residual models
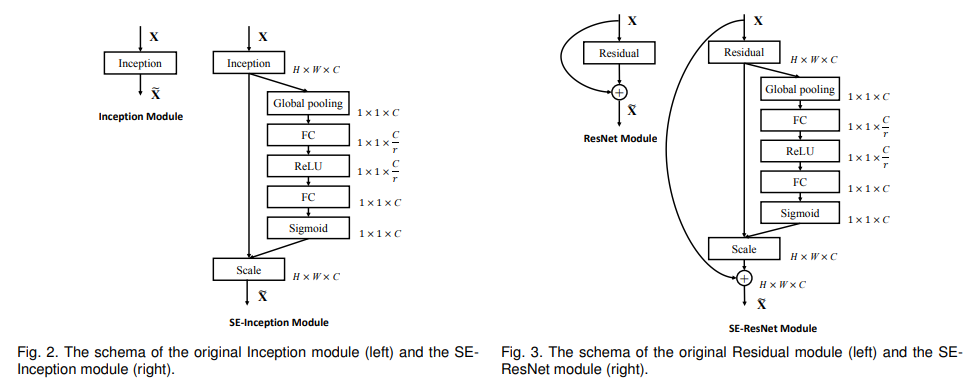(source: [1709.01507] Squeeze-and-Excitation Networks)

Performance and Model complexity

The figure below displays three architectures: ResNet-50 on the left, SE-ResNet-50 in the middle, and SE-ResNeXt-50 with a 32×4d template on the right. The shapes and operations of a residual building block, along with specific parameter settings, are listed inside the brackets. The number of stacked blocks in a stage is shown outside the brackets. Additionally, the inner brackets followed by "fc" indicate the output dimension of the two fully connected layers within an SE module.

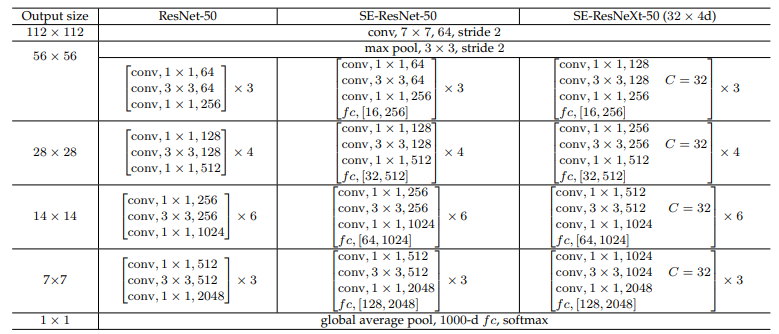
(source: [1709.01507] Squeeze-and-Excitation Networks)

The table below shows Single-crop error rates (%) on the ImageNet validation set and complexity comparisons. The original column represents the results reported in the original papers, while the re-implementation column shows scores obtained after re-training the baseline models for fair comparison. The SENet column indicates the corresponding architectures with SE blocks added. The numbers in brackets indicate the performance improvement over the re-implemented baselines.

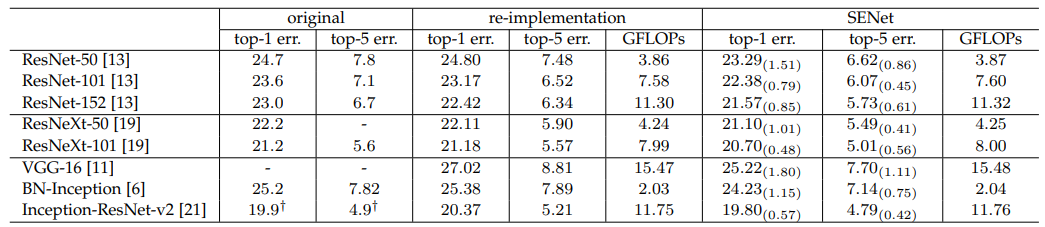
(source: [1709.01507] Squeeze-and-Excitation Networks)

Each SE block involves a global average pooling operation in the squeeze phase, two small fully connected (FC) layers in the excitation phase, and an inexpensive channel-wise scaling operation.

When the reduction ratio (r) is set to 16, SE-ResNet-50 requires approximately 3.87 GFLOPs, representing a 0.26% relative increase compared to the original ResNet-50. Despite this slight additional computational burden, SE-ResNet-50 achieves higher accuracy than ResNet-50 and even approaches the performance of a deeper ResNet-101 network, which requires approximately 7.58 GFLOPs.

In practical terms, a single pass forward and backward through ResNet-50 takes 190 milliseconds, while SE-ResNet-50 takes 209 milliseconds with a training minibatch of 256 images. These timings were performed on a server with 8 NVIDIA Titan X GPUs. This runtime overhead is considered reasonable and may be further reduced as global pooling and small inner-product operations are optimized in popular GPU libraries. Additionally, CPU inference time for each model was benchmarked, and for a 224x224 pixel input image, ResNet-50 takes 164 milliseconds compared to 167 milliseconds for SE-ResNet-50. The small additional computational cost incurred by the SE block is deemed justified due to its contribution to model performance.

Next, the additional parameters introduced by the SE block are considered. These parameters arise solely from the two FC layers of the gating mechanism and constitute a small fraction of the total network capacity. Specifically, the total number of weight parameters introduced by these FC layers is given by the equation:

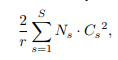
Where r denotes the reduction ratio, S refers to the number of stages, Cs denotes the dimension of the output channels, and Ns denotes the number of repeated blocks for stage s. When bias terms are used in FC layers, the introduced parameters and computational cost are typically negligible.

SE-ResNet-50 introduces approximately 2.5 million additional parameters beyond the approximately 25 million parameters required by ResNet-50, resulting in a roughly 10% increase. However, most of these parameters come from the final stage of the network, where the excitation operation is performed across the largest number of channels. It was found that removing this relatively costly final stage of SE blocks incurs only a small performance cost (<0.1% top-5 error on ImageNet) and reduces the relative parameter increase to approximately 4%. This reduction may be useful in cases where parameter usage is a key consideration.

Overall, considering the improved performance and the relatively small increase in computational burden and parameters, the SE block design offers a favorable trade-off between performance enhancement and model complexity.

Benefits of the SE Block:

The integration of the SE block brings several benefits to CNNs:

1. Adaptive Channel Attention: The SE block enables the network to adaptively focus on the most informative channels by assigning higher weights to relevant features. This attention mechanism allows the network to emphasize discriminative features and suppress less useful or noisy ones.
2. Improved Discriminative Power: By explicitly modeling channel-wise relationships, the SE block enhances the ability of CNNs to capture complex patterns and dependencies within the data. This leads to improved discrimination and better feature representation.
3. Efficient and Lightweight: Despite its effectiveness, the SE block introduces minimal computational overhead. The global average pooling operation reduces the computational complexity by reducing the spatial dimensions, while the subsequent fully connected layers introduce only a marginal increase in model parameters.
4. Compatibility and Flexibility: The SE block can be seamlessly integrated into existing CNN architectures, providing a modular and flexible approach for improving performance. It can be incorporated into various network depths and configurations, making it applicable across a wide range of tasks and datasets.

Alternatives to SE blocks

Alternative blocks or mechanisms exist that can also enhance the performance of CNNs, such as the attention mechanism. The attention mechanism allows the network to selectively focus on specific regions or features of the input data, enabling more efficient and effective learning. Self-attention mechanisms, such as the Transformer architecture, have gained popularity in natural language processing tasks and have been adapted to computer vision tasks as well. These attention-based mechanisms can complement or serve as alternatives to the SE block, depending on the specific requirements and characteristics of the problem at hand.

Conclusion

In conclusion, the Squeeze and Excitation (SE) block has emerged as a powerful architectural unit for enhancing Convolutional Neural Networks (CNNs). By capturing and emphasizing important channel-wise information, the SE block improves the discriminative power of CNNs, leading to enhanced performance in various computer vision tasks. Its adaptive channel attention, improved feature representation, efficiency, and compatibility make it a valuable tool for researchers and practitioners seeking to improve the accuracy and effectiveness of their CNN models. While the SE block is an effective solution, alternative mechanisms such as attention-based approaches also offer enhancements to CNNs and can be considered based on the specific requirements of the problem. As the field of computer vision continues to advance, the SE block stands as a significant contribution in the pursuit of more powerful and efficient CNN architectures.

References

J. Hu, L. Shen, S. Albanie, G. Sun, and E. Wu, "Squeeze-and-Excitation Networks," arXiv:1709.01507v4 [cs.CV], Sep. 2017.