
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 15 minutes
Ternary Search Tree is a special type of trie data structure and is widely used as an low memory alternative to trie in a vast range of applications like spell check and near neighbour searching. To understand Ternary search tree, we should have an idea about what trie is. By definition: a trie, also called digital tree, radix tree or prefix tree is a kind of search tree—an ordered tree data structure used to store a dynamic set or associative array where the keys are usually strings.
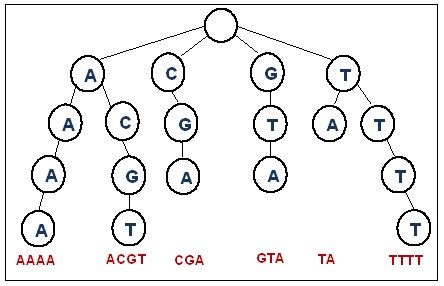
Similarly we are going to use Ternary Search Tree to store keys which are essentially strings but there is a slight change in structure. In trie generally there are 26 child associated to a node (considering english alphabets only) but as the name suggests, in Ternary Search Tree every node can have a maximum of 3 childs only. We will see how this affects the working of normal trie.
Representation
Unlike trie, we don't need 26 pointers for Ternary Search Tree representation. Every node in Ternary Search Tree have 3 pointers:
- left
- middle
- right.
Apart from the pointers every node also have a data field or a character (in case of dictionary or strings) and a flag bit to mark the end of the string.
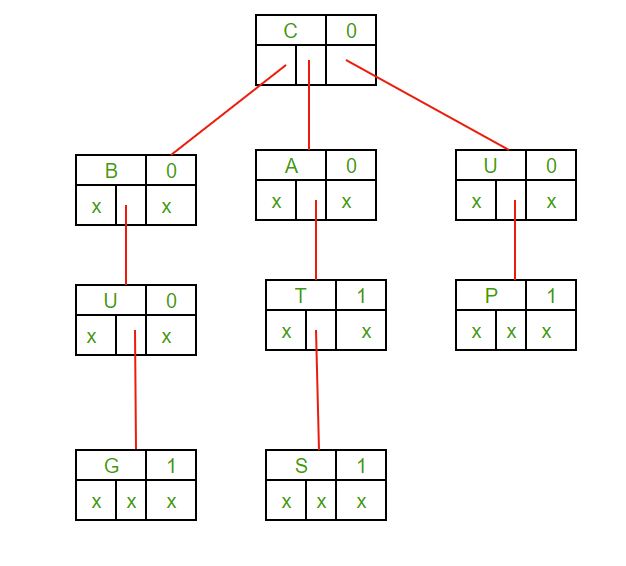
In above image there is a example of a Ternary Search Tree constructed form strings: CAT, BUG, CATS and UP. So a total of five fields are required for the representation of a Ternary Search Tree:-
1. Left pointer
2. Mid Pointer
3. Right Pointer
4. Data field or Character
5. Flag bit (0 or 1)
One of the advantage of using ternary search trees over tries is that ternary search trees are a more space efficient. Tries are suitable when there is a proper distribution of words over the alphabets so that spaces are utilized most efficiently. Otherwise ternary search trees are better. Ternary search trees are efficient to use (in terms of space) when the strings to be stored share a common prefix.
Insertion and Searching
Insertion and searching operations are very easy in ternary search trees. At every point just a character comparison is required to make the proper decision. When we are moving in tree we check the current character in our string with the character stored in the node. Inserting and searching are kind of fundamentally same in ternary search trees. While comparing 3 cases can occur:-
- If current character is smaller than value in node move left.
- If current character is greater than value in node move right.
- If current character is equal to the value in node move to mid.
While inserting if we reach a null node or leaf node, we just allocate memory and add a new one there and repeat. On the other hand, if we reach a null node while searching then the string is clearly not present and if we reach suitable node while searching then the flag bit comes into play. If its set then the searched string is found otherwise not.
Deletion
If you have not noticed, TST is a kind of prefix tree because strings havibg common prefixes have clubbed together in the tree. So, deletion operation should be performed carefully so that it doesn't remove any other string or change them. There are 4 cases when performing deletion in TST:-
- When string to be deleted is not present, then the tree is unmodified.
- When string doesn't share prefix with any other string then delete all nodes correspoding to that string.
- When whole string is prefix of another string then just unmark the node.
- When string share some prefix with another string then remove nodes till they are not common.
Complexity
Average-case time:-
Look-up : O(log n)
Insertion : O(log n)
Deletion : O(log n)
Worst-case time:-
Look-up : O(n)
Insertion : O(n)
Deletion : O(n)
Implementation
C++ implementation of Ternary Search Tree is given below:-
#include <iostream>
#include <vector>
using namespace std;
struct Node{ // struture for a node in TST
char key;
Node* left = nullptr;
Node* right = nullptr;
Node* mid = nullptr;
bool flag = false; // to mark the node that a string ends at the node
Node(char x){ // constructor to initialize value of node
key = x;
}
};
Node* insert_node(Node* root, string &s, int ind){
if(root == nullptr)
root = new Node(s[ind]); // allocate memory for new node
if(ind < s.length()-1){
if(s[ind] < root ->key) // if current character is smaller
root ->left = insert_node(root ->left, s, ind);
else if(s[ind] > root ->key) // if current character is greater
root ->right = insert_node(root ->right, s, ind);
else root ->mid = insert_node(root ->mid, s, ind+1); // if current character is equal
}
else root ->flag = true; // mark node at the end of string
return root;
}
Node* built_Tree(vector<string> &str){
Node *root = nullptr;
for(string s : str){
root = insert_node(root, s, 0);
}
return root;
}
bool search(Node *root, string s){
Node *prev = root;
for(char c : s){
while(root && root ->key != c){ // searching for appropriate node
prev = root;
root = c < root ->key? root ->left : root ->right;
}
if(root){ // if character matches follow the mid link
prev = root;
root = root ->mid;
}
else return false;
}
return prev ->flag; // if the node is marked then string is found
}
void traverse_tree(Node *root, string &out){ // utility function to print strings in TST
if(root){
traverse_tree(root ->left, out); // Traversing left sub-tree
out.push_back(root ->key); // appending current character
if(root ->flag) cout <<out <<"\n"; // if string ends here
traverse_tree(root ->mid, out); // Traversing mid sub-tree
out.pop_back(); // removing last character
traverse_tree(root ->right, out); // Traversing right sub-tree
}
}
int main(){
int k; // number of initial strings
cin >>k;
vector<string> str(k);
for(int i = 0; i < k ;i++)
cin >>str[i];
Node *root = built_Tree(str);
string out, in;
int op = 1;
while(op){
cin >>op;
switch(op){
// To insert new string
case 1: cin >>in;
root = insert_node(root, in, 0);
break;
// To search a string in TST
case 2: cin >>in;
if(search(root, in))
cout <<"String Found!!!\n";
else cout <<"String Not Found!!!\n";
break;
// To traverse TST
case 3: traverse_tree(root, out);
break;
// To break the loop
case 4: op = 0;
break;
default:cout <<"Invalid Option!!!\n";
op = 1;
}
}
return 0;
}
Applications
Ternary search trees can be used to solve many problems in which a large number of strings must be stored and retrieved in an arbitrary order. Some of the most common or most useful of these are below:
- Anytime a trie could be used but a less memory-consuming structure is preferred.
- A quick and space-saving data structure for mapping strings to other data.
- To implement auto-completion.
- As a spell check.
- Near-neighbor searching (of which spell-checking is a special case)
- As a database especially when indexing by several non-key fields is desirable.
- In place of a hash table.
