
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Topological Sort of a directed graph is a linear ordering of its vertices such that for every directed edge u->v, vertex u comes before v in the ordering. In the Topological sort, a process can start when it has 0 prerequisites. In this article, we have covered various Applications of Topological Sort in depth.
In this image, the graph has no vertex with zero prerequisites. For more details, go through this article: Topological sort.
Applications
The Applications of Topological Sort are:
- Finding cycle in a graph
- Operation System deadlock detection
- Dependency resolution
- Sentence Ordering
- Critical Path Analysis
- Course Schedule problem
- Other applications like manufacturing workflows, data serialization and context-free grammar.
The details are as follows:
1. Finding cycle in a graph
A topological ordering is possible only for directed acyclic graph(DAG). For a cyclic graph topological ordering is not possible.

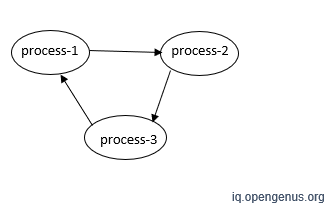
In the figure above (process-1 → process-2), process-2 can be started only when process-1 is already finished. We can say that process-2 depends on process-1, process-3 on process-2, and process-1 on process-3.
If the given graph contains a cycle, then there is at least one vertex will break topological order. If topological sort isn't defined then we can say that the graph is cyclic.
2. Operation System deadlock detection
Deadlock is a state in which a process in a waiting state and another waiting process is holding the demanded resource.
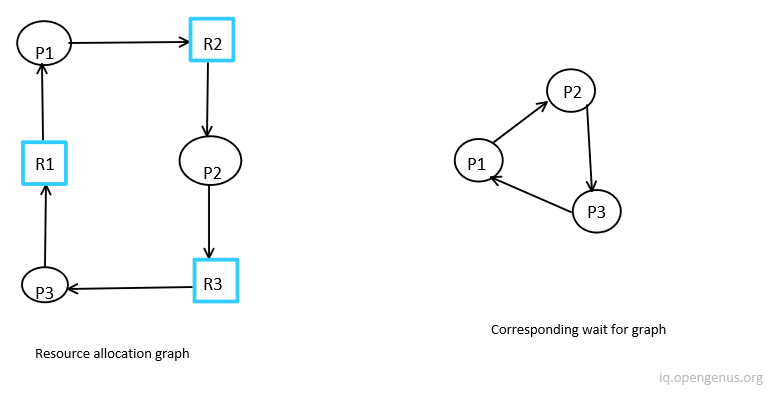
Here, process P1 holds resource R1, process P2 holds resource R2, process P3 holds resource R3, and process P1 is waiting for R2, process P2 is waiting for R3 and process P3 waiting for R1, then process P1, process P2 and process P3 will be in a deadlock. Topological sorting is used here to identify a cycle. If the wait-for graph has a cycle, then there is deadlock.
3. Dependency resolution:
Suppose, A class extends B class. Then B has a dependency on A, and A must be compiled before B.
What happens if A extends B and B also extends A in java? In this
case, the java compiler tries to detect circular dependency.
public class A extends B {
// some code
}
public class B extends A {
// some code
}
Here B is the subclass of A and A is the subclass of B. This relationship is not possible. Java compiler shows an error message.
4. Sentence Ordering:
A set of n documents D={d1,d2...,dn} and the number of sentences in a document is vi,where ∀i,vi>=1. If a random order o=[o1,....ovi] and a set of vi sentences in a random order is {So1,So2,...,Sovi}. Then the task is to find the right order of the sentences o*={o*1,...o*vi}.
A set of constraints Ci represent the relative ordering between every pair of sentences in di where
|Ci|=(vi×(vi-1))/2.
For example, if a document has three sentences in the correct order s1 < s2 < s3, then we have three set of constraints {s1 < s2, s1 < s3, s2 < s3}
The order of the sentences can be represented using a DAG. Here the sentences(Si) represent the vertices, and the edges represent the ordering between sentences.
For example, if we have a directed edge between S1 to S2, then S1 must come before S2. Topological sort can produce an ordering of these sentences (Sentence ordering).
5. Critical Path Analysis:
Critical path analysis is a project management technique. It is used to find the minimum time a project can take and the dependencies of each activity on others. The completion of the project requires the completion of some activities. An activity may have some predecessor activities. It is mandatory to finish the predecessor activities to start a new activity. The critical path calculates the longest path of the activity graph. Activities represent vertices, and edges represent the preceding relationship between them. Activities are listed in topological order.
The critical path algorithm is also used to find the Hamiltonian path in a DAG. The Hamiltonian path is a path in a graph(undirected or directed graph) that visits each vertex exactly once. If a Hamiltonian path exists, the topological order is unique.
6. Course Schedule problem:
There are some courses and they may have some prerequisite courses. One can finish courses in some order.
Prerequisites of course:
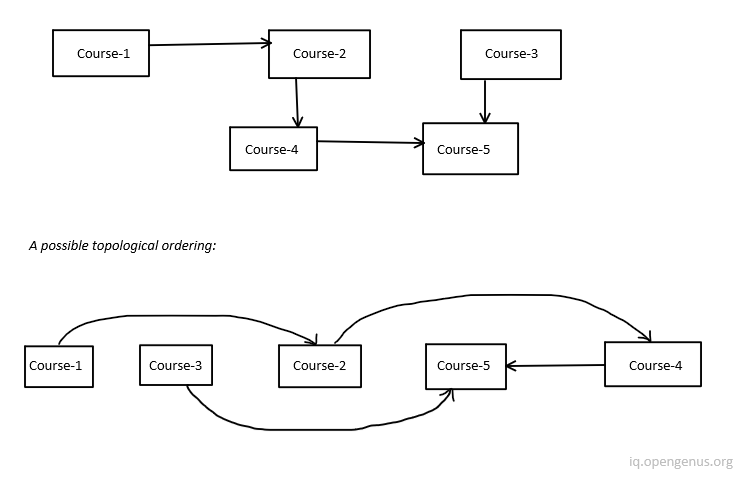
Some other applications of the topological sort are manufacturing workflows, data serialization, context-free grammar and many more.
With this article at OpenGenus, you must have a strong idea of the applications of Topological Sort in real life problems and software systems.
